
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 8. Найти общее решение и фундаментальную систему решений
ТР1: “АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ”
Задача 1. Вычислить определитель.
Задача 2. Даны матрицы 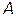 и
и 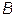 . Найти матрицу
. Найти матрицу  .
.
Задача 3. Найти произведение матриц 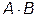 . Существует ли
. Существует ли
произведение 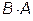 ? Почему?
? Почему?
Задача 4. Найти обратную матрицу для матрицы 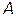 . Сделать проверку.
. Сделать проверку.
Задача 5. Решить матричное уравнение.
Задача 6. Найти ранг матрицы.
Задача 7. Решить систему линейных уравнений:
1) по формулам Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
Задача 8. Найти общее решение и фундаментальную систему решений
для системы уравнений.
Задача 9. Написать разложение вектора 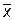 по векторам
по векторам 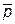 ,
, 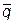 и
и 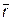 .
.
Задача 10-16. Условия приведены в задании.
ВАРИАНТ 1
1. 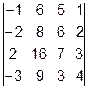 2.
2. 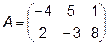 ,
, 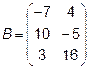 ,
, 
3. 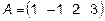 ,
, 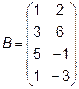 4.
4. 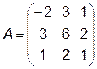 5.
5. 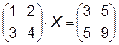
6. 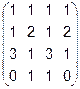 7.
7. 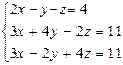 8.
8. 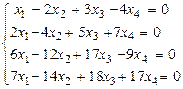
9. 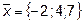 ,
, 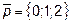 ,
, 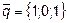 и
и 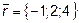
10. Вычислить проекцию вектора  на направление вектора
на направление вектора 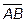 ,
,
где 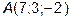 ;
; 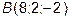 .
.
11. Векторы 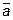 и
и 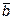 образуют угол в
образуют угол в 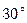 ,
, 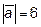 ,
, 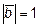 . Найти длину
. Найти длину
вектора 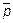 , если
, если 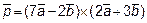 .
.
12. Лежат ли точки 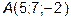 ,
, 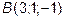 ,
, 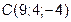 и
и  в одной
в одной
плоскости?
13. Составить уравнения сторон треугольника, зная одну из его вершин
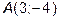 и уравнения двух высот:
и уравнения двух высот: 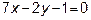 и
и 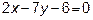 .
.
14. Написать уравнение плоскости, проходящей через ось 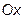 и точку
и точку
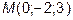 .
.
15. Составить уравнение прямой, которая проходит через точку 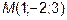
перпендикулярно к вектору 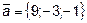 и пересекает прямую
и пересекает прямую
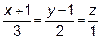 .
.
16. Принадлежит ли прямая 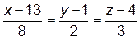 плоскости
плоскости 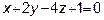 ?
?
ВАРИАНТ 2
1. 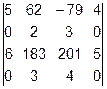 2.
2. 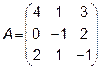 ,
, 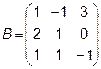 ,
, 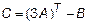
3. 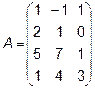 ,
, 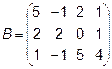 4.
4. 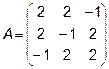 5.
5. 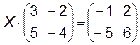
6. 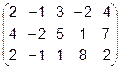 7.
7. 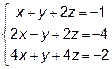 8.
8. 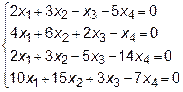
9. 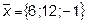 ,
, 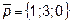 ,
, 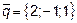 и
и 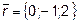
10. Найти единичный вектор, перпендикулярный векторам 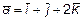 и
и
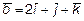 .
.
11. Сила 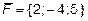 приложена к точке
приложена к точке 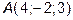 . Определить момент
. Определить момент
этой силы относительно точки 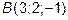 .
.
12. Какую тройку (левую или правую) образуют векторы 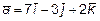 ,
,
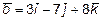 и
и 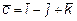 ?
?
13. Составить уравнения сторон треугольника, зная одну его вершину 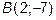 ,
,
а также уравнения высоты 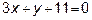 и медианы
и медианы 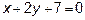 ,
,
проведенных из различных вершин.
14. Написать уравнение плоскости, проходящей через точку 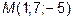 и
и
отсекающей от осей координат положительные и равные отрезки.
15. Составить каноническое уравнение прямой, лежащей в плоскости 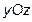 ,
,
проходящей через начало координат и перпендикулярной к прямой
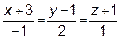 .
.
16. Найти угол между прямой 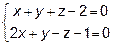 и плоскостью, проходящей
и плоскостью, проходящей
через точки 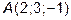 ,
, 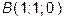 ,
, 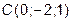 .
.
ВАРИАНТ 3
1. 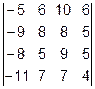 2.
2. 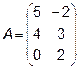 ,
, 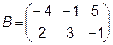 ,
, 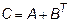
3. 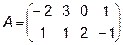 ,
, 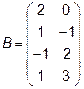 4.
4. 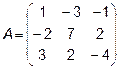 5.
5. 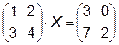
6. 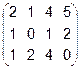 7.
7. 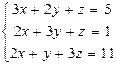 8.
8. 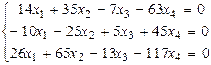
9. 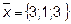 ,
, 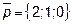 ,
, 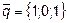 и
и 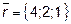
10. При каком t векторы 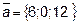 и
и 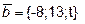 будут взаимно
будут взаимно
перпендикулярны?
11. Вычислить площадь треугольника, построенного на векторах 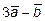 и
и
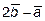 , если
, если 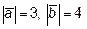 , угол между векторами
, угол между векторами 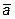 и
и 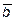 равен
равен 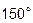 .
.
12. Компланарны ли векторы 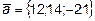 ,
, 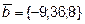 и
и 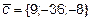 ?
?
13. Через точку пересечения прямых 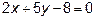 и
и 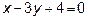 провести
провести
прямую, которая, кроме того, 1) проходит через начало координат;
2) параллельна оси абсцисс; 3) параллельна оси ординат;
4) проходит через точку 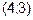 .
.
14. Написать уравнение плоскости, проходящей через точки М(1; 2; 0) и
N(2; 1; 1) параллельно вектору  (3; 0; 1).
(3; 0; 1).
15. Составить уравнение прямой, проходящей через точку M (3; -2; 0) перпен-
дикулярно к прямой 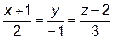 и расположенной в плоскости
и расположенной в плоскости 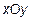 .
.
16. Составить уравнение прямой, проходящей через точки пересечения
плоскости 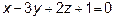 с прямыми
с прямыми 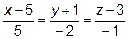 и
и
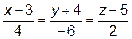 .
.
ВАРИАНТ 4
1. 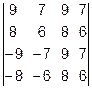 2.
2. 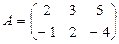 ,
, 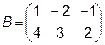 ,
, 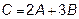
3. 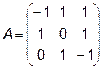 ,
, 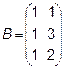 4.
4. 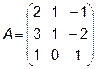 5.
5. 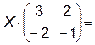
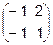
6. 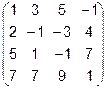 7.
7. 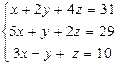 8.
8. 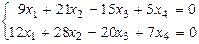
9. 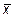 ={11; 5; -3},
={11; 5; -3}, 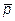 ={1; 0; 2},
={1; 0; 2}, 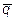 ={-1; 0; 1} и
={-1; 0; 1} и 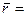 {2; 5; -3}
{2; 5; -3}
10. Доказать ,что точки А(1; -1; 1), B(1; 3; 1), C(4; 3; 1), D(4; -1; 1) являются
вершинами прямоугольника. Вычислить длину его диагоналей.
11. Вычислить площадь треугольника ABC, вершины которого лежат в точках
А(2; 3; 4), B(4; 3; 2), и C(1; 1; 1).
12. При каком значении 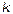 точки А(1; 0; 3), B(-1; 3; 4), C(1; 2; 1), и D(
точки А(1; 0; 3), B(-1; 3; 4), C(1; 2; 1), и D( 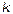 ; 2; 5)
; 2; 5)
лежат в одной плоскости?
13. Написать уравнение прямой, проходящей через точку пересечения прямых
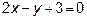 и
и 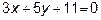 и через точку A(2; 1).
и через точку A(2; 1).
14. Даны координаты вершин тетраэдра А(2; 0; 0), B(5; 3; 0), C(0; 1; 1),
D(-2; -4; 1). Найти двугранный угол между гранями ABC и ABD.
15. При каком значении 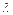 прямые
прямые 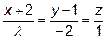 и
и 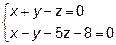
параллельны?
16. Составить уравнение прямой, проходящей через точку А(4; 0; -1) и
пересекающей две данные прямые 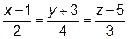 и
и 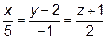 .
.
ВАРИАНТ 5
1. 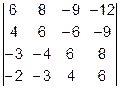 2.
2. 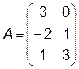 ,
, 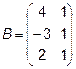 ,
, 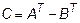
3. 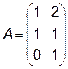 ,
, 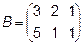 4.
4. 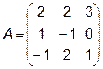 5.
5. 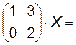
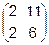
6. 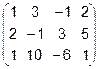 7.
7. 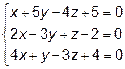 8.
8. 
9. 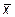 ={13; 2; 7},
={13; 2; 7}, 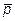 ={5; 1; 0},
={5; 1; 0}, 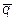 ={2; -1; 3} и
={2; -1; 3} и 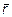 ={1; 0; -1}
={1; 0; -1}
10. В прямоугольном треугольнике АВС углы при вершинах А и С равны 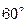 и
и
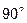 , а длина гипотенузы равна 2. Вычислить
, а длина гипотенузы равна 2. Вычислить 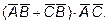
11. Найти вектор 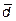 , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 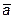 ={0; -1; 2} и
={0; -1; 2} и
 ={1; 3; 3} и удовлетворяет условию
={1; 3; 3} и удовлетворяет условию 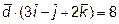 .
.
12. Вычислить объем треугольной пирамиды с вершинами A(0; 0; 1), B(2; 3; 5),
C(6; 2; 3), D(3; 7; 2).
13. Вычислить координаты вершины ромба, если известны уравнения двух его
сторон: x + 2y = 4 и x + 2y = 10 , и уравнение одной из его диагоналей:
y = x + 2 .
14. Найти уравнение плоскости, проходящей через точки М(1; 1; 1) и N(-1; 1;-1)
параллельно прямой , определяемой точками А(5; -2; 3) и В(6; 1; 0).
15. При каком значении D прямая 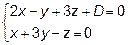 проходит через начало
проходит через начало
координат?
16. Найти точку , симметричную точке А(3; -1; 4) относительно прямой
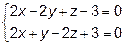 .
.
ВАРИАНТ 6
1. 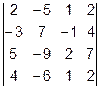 2.
2. 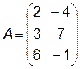 ,
, 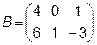 ,
, 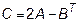
3. 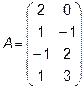 ,
, 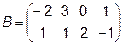 4.
4. 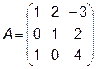
5. 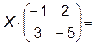
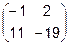
6. 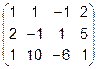 7.
7. 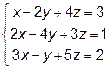 8.
8. 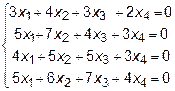
9. 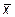 ={2; 7; 5},
={2; 7; 5}, 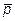 ={1; 0; 1},
={1; 0; 1}, 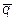 ={1; -2; 0} и
={1; -2; 0} и 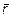 ={0; 3; 1}
={0; 3; 1}
10. Даны точки А(0; -3; 4), В(2; 5; -1) и С(-4; 2; -2). Вычислить скалярное
произведение векторов  и
и 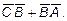
11. Найти длину высоты треугольника АВС, опущенной из вершины С на
сторону АВ, если A(2; 3; 4), B(4; 3; 2) и C(1; 1; 1).
12. Какую тройку (правую или левую) образуют векторы 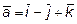 ,
,
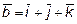 и
и 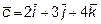 ?
?
13. Найти вершины прямоугольного равнобедренного треугольника, если дана
вершина прямого угла С(3; -1) и уравнение гипотенузы 3x – y + 2 = 0.
14. Составить уравнение плоскости, проходящей через перпендикуляры,
опущенные из точки А(2; 0; 1) на плоскости x – 3y +2z = 0 и 2x – y + 2z = 0.
15. Написать каноническое уравнение прямой, проходящей через точку
М(2; 1; 3), параллельно прямой x = 3+t , y = 3t, z = 2-t.
16. Найти угол между прямой, проходящей через точки А(-1; 0; -5) и В(1; 2; 0),
и плоскостью x – 3y + z + 5 = 0.
ВАРИАНТ 7
1 
. 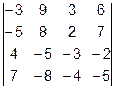 2.
2. 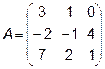 ,
, 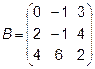 ,
, 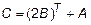
3. 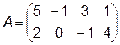 ,
, 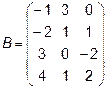 4.
4. 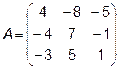
5. 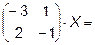
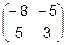
6. 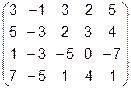 7.
7. 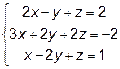 8.
8. 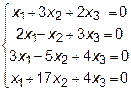
9. 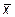 ={-9; 5; 5},
={-9; 5; 5}, 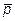 ={4; 1; 1},
={4; 1; 1}, 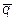 ={2; 0; -3} и
={2; 0; -3} и 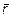 ={-1; 2; 1}
={-1; 2; 1}
10. Треугольник АВС задан координатами своих вершин А(-1; -2; 4), В(-4; -2; 0)
и С(3; -2; 1). Определить его внешний угол при вершине В.
11. Раскрыть скобки и упростить выражение:
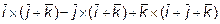 .
.
12. Вычислить объем параллелепипеда, построенного на векторах
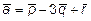 ,
, 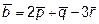 ,
, 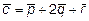 , где
, где  и
и 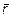 - взаимно
- взаимно
перпендикулярные орты.
13. Стороны АВ и ВС параллелограмма заданы уравнениями 2x – y + 5 = 0 и
x – 2y + 4 = 0, диагонали его пересекаются в точке М(1; 4). Найти уравнение
сторон CD и AD.
14. Найти уравнение плоскости, проходящей через точку М(2; -3; 1)
параллельно векторам 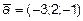 и
и 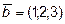 .
.
15. Даны вершины треугольника А(1; 0; -1), В(2; 1; 3), С(0; -1; 1). Составить
уравнение высоты, опущенной из вершины В на сторону АС.
16. Найти основание перпендикуляра, опущенного из точки А(-1; 3; 2) на
плоскость 2x – y + z + 3 = 0.
ВАРИАНТ 8

1. 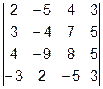 2.
2. 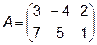 ,
, 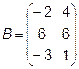 ,
, 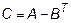
3. 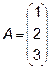 ,
, 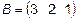 4.
4. 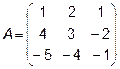 5.
5. 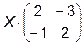 =
= 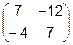
6. 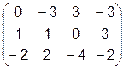 7.
7. 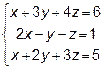 8.
8. 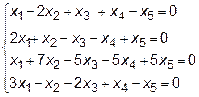
9. 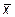 ={-5; -5; 5},
={-5; -5; 5}, 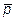 ={-2; 0; 1},
={-2; 0; 1}, 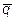 ={1; 3; -1} и
={1; 3; -1} и 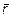 ={0; 4; 1}
={0; 4; 1}
10. Найти координаты вектора 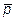 , коллинеарного вектору
, коллинеарного вектору 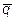 ={3; -4; 0}, если известно, что вектор
={3; -4; 0}, если известно, что вектор 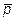 образует с осью
образует с осью 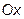 тупой угол и
тупой угол и 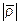 =10.
=10.
11. 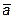 ={3; 1; -1},
={3; 1; -1}, 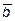 ={-2; 1; 4}. Вычислить
={-2; 1; 4}. Вычислить 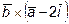 .
.
12. Вычислить объем треугольной пирамиды с вершинами A(0; 0; 1), B(2; 3; 5),
C(6; 2; 3) и D(3; 7; 2).
13. Написать уравнение прямой, проходящей через точку М пересечения
прямых 2x + y + 6 = 0 и 3x + 5y – 15 = 0 и через точку N(1; -2).
14. Найти уравнение плоскости, проходящей через точку М(2; 5; 3) параллельно
плоскости x + 2y - 3z + 2= 0 .
15. При каком значении 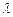 прямые
прямые 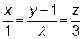 и
и 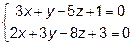
перпендикулярны?
16. Проверить, что прямые 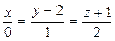 и
и 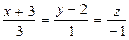 пересекаются.
пересекаются.
Найти уравнение плоскости, в которой они лежат.
ВАРИАНТ 9
1.  2.
2. 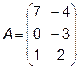 ,
, 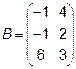 ,
, 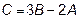
3. 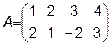 ,
, 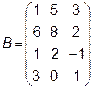 4.
4. 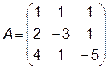 5.
5. 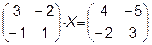
6. 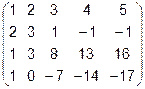 7.
7. 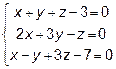 8.
8. 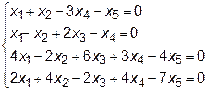
9. 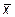 ={13; 2; 7},
={13; 2; 7}, 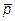 ={5; 1; 0},
={5; 1; 0}, 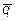 ={2; -1; 3} и
={2; -1; 3} и 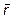 ={1; 0; -1}
={1; 0; -1}
10. По координатам вершин треугольника АВС A(1; 1; -1), B(2; 4; -1) и
C(8; 3; -1) выяснить, является ли он прямоугольным, остроугольным или
тупоугольным.
11. Раскрыть скобки и упростить выражение:
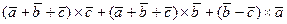 .
.
12. При каком m векторы 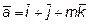 ,
,  и
и 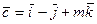
компланарны?
13. В треугольнике АВС даны: уравнение стороны АВ: 3x + 2y = 12, уравнение
высоты BM: x + 2y = 4 , уравнение высоты АМ: 4x + y = 6, где М - точка
пересечения высот. Написать уравнения сторон АС и ВС.
14. Найти уравнение плоскости, проходящей через точки А(2; 3; -1) и В (1; 5; 3)
перпендикулярно плоскости 3x – y + 3z + 15 = 0 .
15. Через точку М(2; -1; 3) провести прямую, параллельную прямой
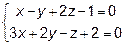 .
.
16. Написать каноническое уравнение прямой, которая проходит через точку
М(3; -2; -4) параллельно плоскости 3x – 2y – 5z – 7=0 и пересекает прямую
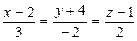 .
.
ВАРИАНТ 10
1. 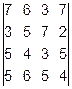 2.
2. 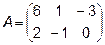 ,
,  ,
, 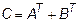
3. 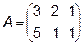 ,
, 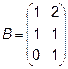 4.
4. 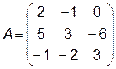 5.
5. 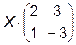 =
= 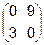
6. 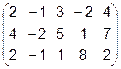 7.
7. 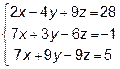 8.
8. 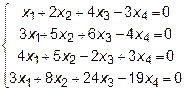
9. 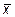 ={-19; -1; 7},
={-19; -1; 7}, 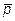 ={0; 1; 1},
={0; 1; 1}, 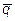 ={-2; 0; 1} и
={-2; 0; 1} и 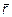 ={3; 1; 0}
={3; 1; 0}
10. Проверить будет ли треугольник АВС (A(1; 2; 3), B(7; 10; 3), C(-1; 3; 1))
прямоугольным?
11. Раскрыть скобки и упростить выражение:
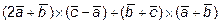 .
.
12. Найти объем параллелепипеда с вершинами в точках A(2; 2; 2), B(4; 3;3),
C(4; 5; 4) и D(5; 5; 6).
13. Дано уравнение 3x + 4y – 12 = 0 стороны АВ параллелограмма ABCD,
уравнение x + 12y - 12 = 0 диагонали АС и середина Е 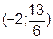 стороны ВС.
стороны ВС.
Найти уравнения сторон ВС, СD и AD.
14. Cоставить уравнение плоскости, проходящей через точку М (2; -3; 5)
перпендикулярно линии пересечения плоскостей 2x + y - 2z + 1 = 0 и
x + y + z –5 = 0 .
15. Из начала координат опустить перпендикуляр на прямую
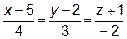 .
.
16. При каком значении 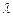 плоскость 5x – 3y +
плоскость 5x – 3y + 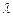 z + 1 = 0 будет параллельна
z + 1 = 0 будет параллельна
прямой 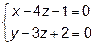 ?
?
ВАРИАНТ 11
1. 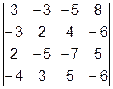 2.
2. 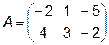 ,
, 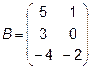 ,
, 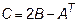
3. 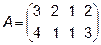 ,
, 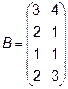 4.
4. 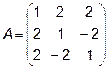 5.
5. 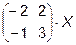 =
= 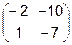
6. 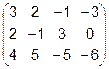 7.
7. 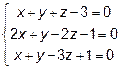 8.
8. 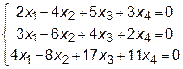
9. 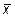 ={3; -3; 4},
={3; -3; 4}, 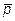 ={1; 0; 2},
={1; 0; 2}, 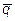 ={0; 1; 1} и
={0; 1; 1} и 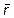 ={2; -1; 4}
={2; -1; 4}
10. Найти работу силы 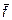 ={4; -1; 1} на перемещении
={4; -1; 1} на перемещении 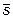 ={5; 3; -2}.
={5; 3; -2}.
11. Вычислить координаты вектора  , перпендикулярного векторам
, перпендикулярного векторам
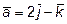 и
и 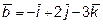 и образующего тупой угол с осью
и образующего тупой угол с осью 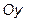 , если
, если
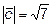 .
.
12. Доказать, что точки A(1; -2; 2), B(1; 4; 0), C(-4; 1; 1) и D(-5; -5; 3) лежат в
одной плоскости.
13. Даны уравнения сторон параллелограмма ABCD: AB: 3x + 4y - 12 = 0,
AD: 5x - 12y - 6 = 0 и середина Е(-2; 1) стороны BC. Найти уравнения двух
других сторон параллелограмма.
14. Написать уравнение плоскости, проходящей через три заданные точки
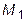 (1; 2; 0),
(1; 2; 0), 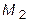 (2; 1; 1),
(2; 1; 1), 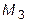 (3; 0; 1).
(3; 0; 1).
15. Через точку А(0; -2; 1) провести прямую так, чтобы она пересекала две
данные прямые 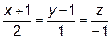 и
и 
16. Найти расстояние от точки А(2; 3; -1) до прямой 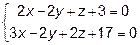 .
.
ВАРИАНТ 12
1. 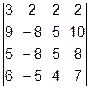 2.
2. 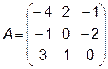 ,
, 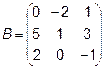 ,
, 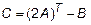
3. 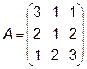 ,
, 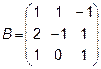 4.
4. 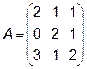 5.
5. 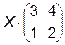 =
= 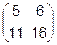
6. 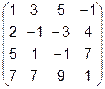 7.
7. 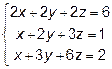 8.
8. 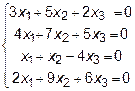
9. 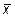 ={8; 0; 5},
={8; 0; 5}, 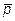 ={2; 0; 1},
={2; 0; 1}, 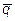 ={1; 1; 0} и
={1; 1; 0} и 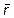 ={4; 1; 2}
={4; 1; 2}
10. Найти скалярное произведение векторов 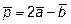 и
и 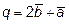 , если
, если
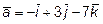 и
и 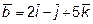 .
.
11. Найти площадь параллелограмма, построенного на векторах 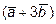 и
и
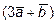 , если
, если 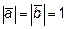 , а угол между векторами
, а угол между векторами 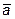 и
и 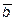 равен
равен 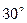 .
.
12. Какую тройку (левую или правую) образуют векторы 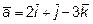 ,
,
 ,
, 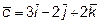 ?
?
13. Даны вершины треугольника А(2; 1), B(-1; -1), C(3; 2). Составить уравнение
высоты, опущенной на сторону ВС, и медианы, проведенной к стороне АС.
14. Плоскость проходит через ось 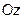 и составляет с плоскостью
и составляет с плоскостью
2x + y - 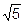 z = 0 угол
z = 0 угол 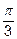 . Найти её уравнение.
. Найти её уравнение.
15. Пересекаются или нет прямые 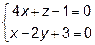 и
и 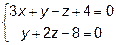 ?
?
16. Найти проекцию точки М(0; 1; 2) на прямую 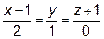 .
.
ВАРИАНТ 13
1. 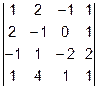 2.
2. 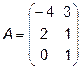 ,
, 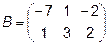 ,
, 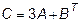
3. 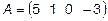 ,
, 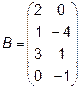 4.
4. 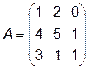 5.
5. 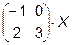 =
= 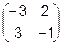
6. 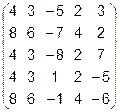 7.
7.  8.
8. 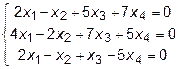
9. 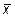 ={3; 1; 8},
={3; 1; 8}, 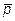 ={0; 1; 3},
={0; 1; 3}, 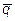 ={1; 2; -1} и
={1; 2; -1} и 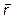 ={2; 0; -1}
={2; 0; -1}
10. Найти угол между векторами 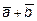 и
и 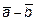 , если
, если 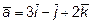 и
и
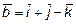 .
.
11. Вычислить площадь параллелограмма, построенного на векторах
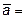 {2; -1; 5} и
{2; -1; 5} и 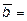 {2; 3; 6} как на сторонах.
{2; 3; 6} как на сторонах.
12. Проверить, компланарны ли векторы 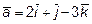 ,
, 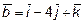 ,
,
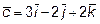 .
.
13. Найти проекцию точки М(1; 1) на прямую 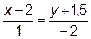 .
.
14. Написать уравнение плоскости, параллельной оси 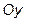 и проходящей через
и проходящей через
точки А(-1; 2; 1) и В(3; 0; 2).
15. Проверить, пересекаются ли прямые 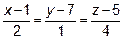 и
и
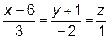 .
.
16. Написать уравнение плоскости, проходящей через прямую
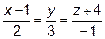 , перпендикулярно плоскости 3x + y – 2z + 5 = 0.
, перпендикулярно плоскости 3x + y – 2z + 5 = 0.
ВАРИАНТ 14
1. 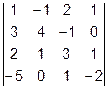 2.
2. 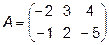 ,
, 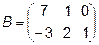 , C=2A-3B
, C=2A-3B
3. 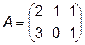 ,
, 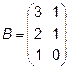
 4.
4. 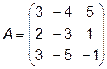 5.
5. 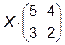 =
= 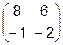
6. 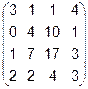 7.
7. 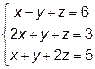 8.
8. 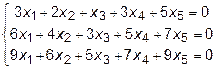
9.  ={8; 1; 12},
={8; 1; 12},  ={1; 2; -1},
={1; 2; -1}, 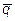 ={3; 0; 2} и
={3; 0; 2} и 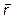 ={-1; 1; 1}
={-1; 1; 1}
10. Даны векторы 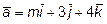 и
и 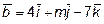 . При каком
. При каком 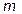 векторы
векторы
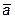 и
и 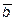 перпендикулярны?
перпендикулярны?
11. Вычислить площадь треугольника с вершинами в точках А(2; 2; 2),
B(4; 0; 3) и C(0; 1; 0).
12. Проверить будут ли компланарны векторы 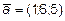 ,
, 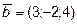 и
и
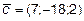 ?
?
13. Найти точку N, симметричную точке М(0; -3) относительно прямой
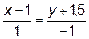 .
.
14. Написать уравнение плоскости, проходящей через ось 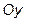 и точку
и точку
M(2; -1; 3).
15. Даны вершины треугольника А(1; 0; 2), B(-2; 3; -1), C(3; -2; 4). Составить
уравнение медианы из вершины В на сторону АС.
16. Через прямую x = 2t + 1, y = -t + 2, z = 3t – 2 провести плоскость
параллельную прямой 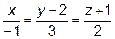 .
.
ВАРИАНТ 15
1. 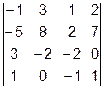 2.
2. 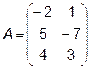 ,
, 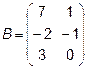 ,
, 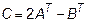
3. 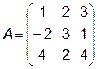 ,
, 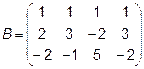 4.
4. 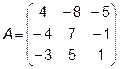
5. 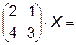

6. 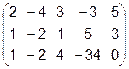 7.
7. 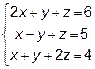 8.
8. 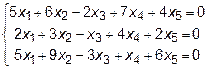
9. 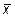 ={-9; -8; -3},
={-9; -8; -3}, 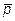 ={1; 4; 1},
={1; 4; 1}, 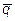 ={-3; 2; 0} и
={-3; 2; 0} и 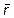 ={1; -1; 2}
={1; -1; 2}
10. Найти скалярное произведение векторов 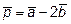 и
и 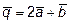 , если
, если
 ,
, 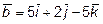 .
.
11. Найти вектор 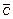 , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 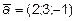 и
и
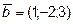 и удовлетворяет условию
и удовлетворяет условию 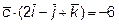 .
.
12. Заданы точки А(1; 2; -2), B(3; 2; -1) , C(0; 1; -2) и D(3; 2; 3). Найти объем
тетраэдра АBCD.
13. Составить уравнения сторон треугольника, зная его вершину С(1; 2), а так-
же уравнения высоты x – 2y + 1 = 0 и медианы 4x + y + 2 = 0, проведенных
из одной вершины.
14. Из точки Р(2; -1; 3) опущен на плоскость перпендикуляр, его основание
М(1; 2; 4). Найти уравнение плоскости.
15. Составить уравнение прямой, которая проходит через точку А(1; -5; 3) и
образует с осями координат углы, соответственно равные 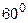 ,
, 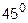 ,
, 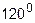 .
.
16. Найдите точку В, симметричную точке А(2; 0; 1) относительно прямой
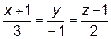 .
.
ВАРИАНТ 16
1. 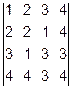 2.
2.  ,
, 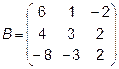 ,
, 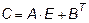
3. 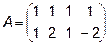 ,
, 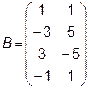 4.
4. 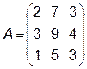 5.
5. 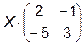 =
= 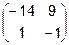
6. 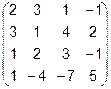 7.
7.  8.
8. 
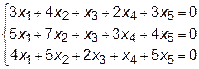
9. 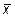 ={-5; 9; -13},
={-5; 9; -13}, 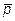 ={0; 1; -2},
={0; 1; -2}, 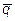 ={3; -1; 1} и
={3; -1; 1} и 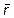 ={4; 1; 0}
={4; 1; 0}
10. Векторы 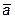 и
и 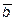 образуют угол
образуют угол 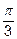 . Найти длину вектора
. Найти длину вектора 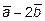 , если
, если
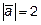 ,
, 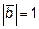 .
.
11. Найти площадь параллелограмма, построенного на векторах 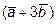 и
и
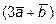 , если
, если 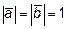 , а угол между векторами
, а угол между векторами 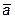 и
и 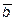 равен
равен 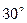 .
.
12. Компланарны ли векторы 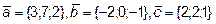 ?
?
13. В треугольнике АВС даны: уравнение стороны АВ: 3x – 4y + 5 = 0,
уравнение высоты АМ: x + 2y – 10 = 0 и высоты BN: 2x – 3y + 4 = 0.
Составить уравнения двух других сторон треугольника.
14. Через линию пересечения плоскостей 4x – y + 3z – 1 = 0 и x + 5y – z +2 = 0
провести плоскость, проходящую через точку M(1; 1; 1).
15. Написать уравнение перпендикуляра, опущенного из точки А(-1; 0; 3) на
прямую 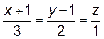 .
.
16. Написать уравнение плоскости, проходящей через прямую
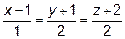 и
и
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|