РЕФЕРАТ. Алгоритм Брандона

Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Кафедра Инженерных систем зданий и сооружений

Инженерно-строительный институт

РЕФЕРАТ

Модели многофакторной регрессии. Метод Брандона.

Руководитель __________ Прокопьев А.П.

подпись, дата инициалы, фамилия

Студент СФ 15-07М, 411514780 ___________ Андреев М.С.

номер группы, зачетной книжки подпись, дата инициалы,фамилия

Красноярск 2016

Алгоритм Брандона

Шаг 1. Вычислить среднее значение выходной характеристики

, .

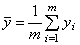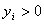Шаг 2. Выполнить преобразование

, .

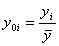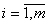Шаг 3. Для пары переменных 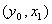, построить зависимости типа 1-16 (см. выше) и по критерию Дарбина-Уотсона (DW) и по величине корреляционного отношения 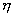(для линейных зависимостей берут коэффициент корреляции 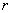) выбирается зависимость, имеющая максимальный уровень спецификации:

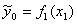Шаг 4. Выполнить преобразование:

, .

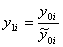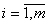Шаг 5. Для пары переменных 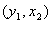выбрать вид зависимости, имеющий максимальный уровень спецификации:

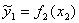Процесс продолжать до исчерпания всех факторов, воздействующих на выходную характеристику.

После определения

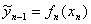строим общую формулу множественной регрессии:

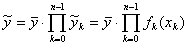Корреляционное отношение считаем по формуле:

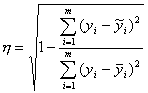Если, например, 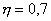, то это означает, что средняя относительная ошибка аппроксимации равна 30%.

Пусть 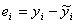. Тогда значение критерия Дарбина-Уотсона определяют по формуле:

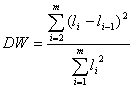Если 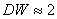, то автокорреляция отсутствует, ес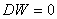ли , или 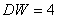, то имеет место полная автокорреляция. Промежуточные результаты проверяют с помощью специальных таблиц, которые можно найти в любом учебнике по эконометрии.

Список используемых источников

1. http://miest.narod.ru/iissvit/rass/vip19.htm

2. http://studme.org/1482111111623/menedzhment/mnogofaktornye_nelineynye_uravneniya_regressii

3. Прикладной регрессионный анализ (многофакторная регрессия). Шашков В.Б. Учебное пособие. — Оренбург: ГОУ ВПО ОГУ, 2003. — 363 с.

4. Прикладной регрессионный анализ (книга 1). Дрейпер Н., Смит Г. 1986. — 366 с.