Ряды Фурье.

Лекции от 10.12 и 17.12.

Ряды Фурье.

1)Общие свойства рядов Фурье.

Пусть 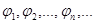- полная ортогональная система функций в пространстве 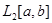. Тогда, согласно определению полноты, любая функция f из этого пространства представима в виде функционального ряда

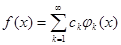, (1)

который называется ее рядом Фурье.

(Строго говоря функции в пространстве 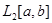определены с точностью до отдельных точек, поскольку значения функции в отдельных точках не влияют на интеграл от нее. Соответственно и равенство функции ряду справедливо для почти всех 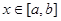, оно может нарушаться в отдельных точках – обычно это точки разрыва f(x), или в крайние точки отрезка.)

Благодаря ортогональности системы функций, нетрудно получить формулу для вычисления коэффициентов ряда. Действительно, умножив скалярно обе части равенства (1) на одну из функций системы , получим равенство

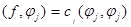откуда следует

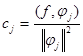(2)

Если в обобщенной теореме Пифагора устремить число слагаемых к бесконечности, то из равенства (1) получится тождество (без строгого доказательства)

, (3)

которое называется равенством Парсеваля.

Рассмотрим частичную сумму ряда Фурье

Благодаря ортогональности системы, оставшаяся часть (остаток) ряда ортогонален этой сумме. Таким образом, можно сказать, что 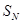представляет собой ортогональную проекцию f на конечномерное подпространство, порожденное базисом 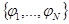. По аналогии с пространством 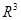, где наилучшим (наиболее близким по расстоянию) приближением вектора к плоскости является его ортогональная проекция на эту плоскость, можно утверждать (без доказательства), что частичная сумма 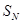является наилучшим приближением (в смысле нормы в 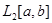) функции f к конечномерному подпространству, порожденному базисом .

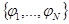Нетрудно также вычислить квадрат нормы отклонения f от этого приближения. Действительно, благодаря обобщенной теореме Пифагора,

откуда следует

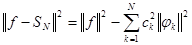. (4)

2)Полная ортогональная система тригонометрических функций.

(Здесь технически удобнее рассматривать отрезок задания функции с центром в 0, хотя нетрудно проверить, что все изложенное ниже можно применить к любому отрезку, если его длину обозначить через 2Т. )

Рассмотрим пространство 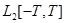и в нем бесконечную систему функций

1, , , , , …, , , …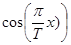

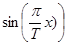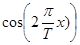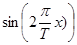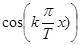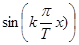Покажем, что эта система является ортогональной.

1 ортогональна всем остальным функциям. Действительно,

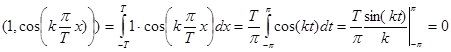
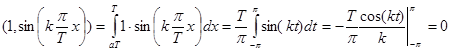
(Здесь и далее пользуемся заменой переменной 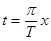, соответственно и ).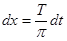

Все косинусы и синусы ортогональны друг другу. Действительно,

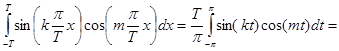
так как, очевидно равны 0 интегралы от обоих слагаемых.

Аналогично, пользуясь тригонометрическими формулами для произведения косинусов и произведения синусов, можно показать, что при 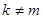все косинусы ортогональны между собой и все синусы ортогональны между собой. Таким образом, данная система тригонометрических функций является ортогональной.

Данная система тригонометрических функций также является полной, то есть образует базис в 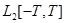. (без доказательства).

3)Тригонометрический ряд Фурье.

Ряд Фурье по введенной выше системе тригонометрических функций называется тригонометрическим рядом Фурье. Этот ряд принято записывать в следующем виде

(5)

Заметим, что данный ряд является периодической функцией с периодом 2T, он продолжает функцию за пределы исходного интервала по периодичности.

Для вычисления коэффициентов этого ряда с помощью формулы (2) нужно, прежде всего, найти квадраты норм базисных функций:

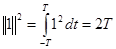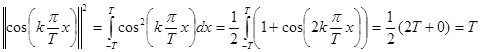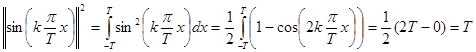Теперь по формуле (2) получаем, что коэффициент при 1 (как первой функции нашего базиса)

то есть 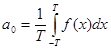. (6)

Аналогично, учитывая, что квадраты норм всех остальных базисных функций равны T, по формуле (2) получаем

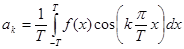(7)

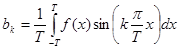(8)

(Заметим, что если в формулу (7) подставить k=0, то получится формула (6). Именно поэтому коэффициент при 1 принято обозначать )

Равенство функции своему ряду Фурье (5) справедливо во всех точках непрерывности f(x) внутри отрезка (-T.T). Если в некоторой точке f(x) имеет разрыв 1 рода (“ступенька” на графике), или такой разрыв получается в крайней точке отрезка при продолжении функции по периодичности, то в такой точке разрыва значение тригонометрического ряда Фурье равно полусумме правостороннего и левостороннего пределов функции в этой точке (то есть значение ряда попадает на середину “ступеньки”) Этот факт называется Теоремой Дирихле, мы примем его без доказательства.

Частичные суммы тригонометрического ряда Фурье называются тригонометрическими многочленами. Они являются периодическими с периодом 2T и являются бесконечно-гладкими (имеют производные любого порядка). Одним из применений тригонометрического ряда Фурье является приближение заданной на ограниченном отрезке кусочно-непрерывной функции тригонометрическими многочленами. Как следует из изложенной выше общей теории рядов Фурье, частная сумма тригонометрического ряда Фурье является в некотором смысле наилучшим приближением к функции в классе тригонометрических многочленов данного порядка.

Для оценки близости функции f(x) к частной сумме ее тригонометрического ряда Фурье 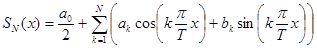можно использовать формулу (4), которая, с учетом найденных выше значений квадратов норм базисных функций, дает

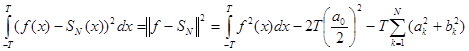. (9)

4)Тригонометрические ряды Фурье только по косинусам и только по синусам.

В рассматриваемой системе тригонометрических функций константа и все косинусы являются четными функциями, а все синусы – нечетными. Таким образом, тригонометрический ряд Фурье одновременно раскладывает функцию на сумму четной и нечетной части. Если же исходная функция является четной, то нечетная часть исчезает (все 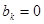). Если же она является нечетной, то исчезает четная часть (все 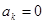в том числе 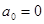). (Строго говоря, это следует из формул (6) - (8), поскольку интеграл от нечетной функции по симметричному промежутку всегда равен 0.)

Предположим теперь, что исходная функция задана на интервале [0, T]. Для ее представления в виде тригонометрического ряда Фурье можно поступить одним из 3 способов.

1)Разложить ее в обычный ряд Фурье с периодом T в . Разложение будет выглядеть так же, как разложение, описанное выше, но с заменой T на T/2 во всех формулах (интегралы при этом берутся по отрезку [0, T])

2) Продолжить функцию по четности (f(-x)=f(x)) на интервал [-T, 0). В этом случае все 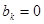, и получится разложение функции в 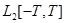в ряд Фурье только по косинусам:

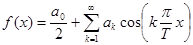, (10)

где 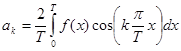(k=0, 1, 2, …) (11)

(Последняя формула получается из (6)-(7) благодаря тому, что интеграл от четной функции по симметричному промежутку равен удвоенному интегралу по его положительной части.)

Оценка (9) близости функции f(x) к частной сумме ряда в этом случае примет вид

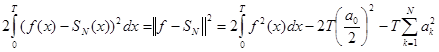. (12)

3) Продолжить функцию по нечетности (f(-x)=-f(x)) на интервал [-T, 0). В этом случае все 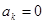и получится разложение функции в 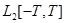в ряд Фурье только по синусам:

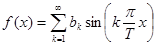, (12)

где 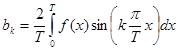(13)

(Последняя формула получается из (8) так же, как (11) из (6)-(7).)

Оценка (9) близости функции f(x) к частной сумме ряда в этом случае примет вид

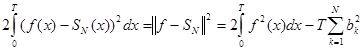. (13)