Пространство . Ортогональные системы функций.

Лекция от 03.12.

Пространство . Ортогональные системы функций.

Прежде чем перейти к новому типу функциональных рядов – рядам Фурье, рассмотрим некоторые теоретические вопросы, обосновывающие ряд полезных свойств таких рядов и формулы вычисления их коэффициентов.

1)Пространство .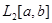

Рассмотрим множество вещественных функций, заданных и кусочно-непрерывных на замкнутом отрезке [a, b]. Для них естественным образом определены операции сложения и умножения на число, которые не выводят за пределы этого множества. Таким образом, это множество функций образует линейное пространство. Введем в этом линейном пространстве скалярное произведение функций f и g:

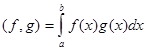Мы имеем право назвать это скалярным произведением, потому что оно обладает теми же свойствами, что и известное нам скалярное произведение векторов в 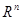, а именно:

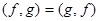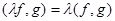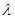, где -любое число,

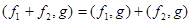
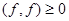(и обращается в 0 только для функции практически везде равной нулю.

Все эти свойства легко получаются из известных свойств определенного интеграла.

Описанное выше множество функций с указанным скалярным произведением называется пространством .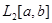

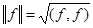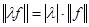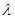Если в некотором линейном пространстве определено скалярное произведение, то сразу естественным образом вводится понятие нормы . Из этого определения сразу следует, что норма не отрицательна и обращается в 0 только для функции практически везде равной нулю. Кроме, того, очевидно, что , где -любое число.

Таким образом, норма в пространстве 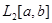определяется формулой

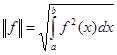Еще одно важное свойство нормы, порожденной скалярным произведением, которое мы примем без доказательства, заключается в выполнении неравенства

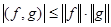
(Для векторов в 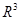такое неравенство очевидно, поскольку скалярное произведение там равно произведению длин векторов на косинус угла между ними).

Используя последнее неравенство, нетрудно также получить известное неравенство треугольника

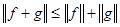Действительно,

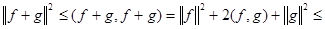
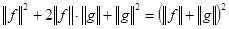Извлекая квадратный корень из обеих частей получившегося неравенства, получим требуемое.

2)Свойство ортогональности.

Два элемента пространства со скалярным произведением называются ортогональными, если их скалярное произведение равно 0.

В пространстве 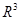ортогональность геометрически означает перпендикулярность векторов.

В любом линейном пространстве со скалярным произведением справедлива обобщенная теорема Пифагора.

Если элементы пространства f и g ортогональны, то

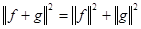Действительно, при равенстве нулю скалярного произведения

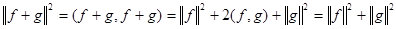Нетрудно проверить, что если один элемент ортогонален к нескольким другим, то он ортогонален к любой их линейной комбинации, в частности к сумме. Благодаря этому свойству обобщенная терема Пифагора с помощью индукции обобщается на любое число слагаемых.

Если элементы пространства 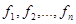попарно ортогональны, то

                              .

3) Ортогональные системы функций.

Из курса Алгебры и геометрии известно, что в пространстве 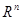существует ортогональный базис из n векторов, точнее всегда можно найти n попарно ортогональных векторов, и тогда любой вектор пространства будет выражаться через их линейную комбинацию. Мы говорим, что пространство 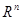имеет размерность n. В отличие от 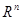, пространство 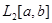является бесконечномерным, то есть ортогональный базис в этом пространстве содержит бесконечное число элементов, а разложение по этому базису представляет собой разложение функции в функциональный ряд. Понятно, не любая бесконечная система попарно ортогональных функций является базисом в 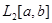. Свойство ортогональной системы функций являться базисом в 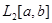называется свойством ее полноты.

    Итак, ортогональным базисом в 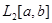является полная ортогональная система функций (которая обязательно содержит бесконечное число элементов).

   Функциональный ряд, который представляет собой разложение некоторой функции из 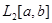по этому базису называется ее рядом Фурье.