Лабораторная работа №3.. Свойства и графики тригонометрических функций.. Ход работы.

Лабораторная работа №3.

Свойства и графики тригонометрических функций.

Цель работы: изучить методы построения графиков тригонометрических функций с помощью окружности, изучить с помощью графика функций свойства тригонометрических функций.

Ход работы.

Задание 1. Построение графика функции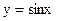

Построение синусоиды выполняется в следующей последовательности:

1. Проводят горизонтальную ось и на ней откладывают отрезок AB (АВ=12 см);

2. Отрезок АВ разделить на 12 равных частей;

3. Слева через точку А вычерчивают окружность, радиус которой равен приблизительно 1/6 АВ (если АВ=12 см, то R = 2 см). Разделить окружность тоже на 12 равных частей (каждую четверть на 3 части, по 30⁰ на каждую часть)

4. Точки деления окружности нумеруют и через них проводят горизонтальные прямые;

5. Из точек деления отрезка АВ восстанавливают перпендикуляры к оси синусоиды;

6. Точки пересечения перпендикуляров с соответствующими горизонтальными прямыми - а1, а2, ... - точки синусоиды;

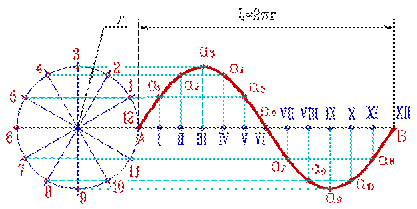
рис. 1

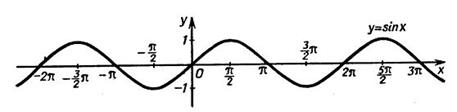Применяя такой метод, получаем график функции на промежутке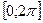

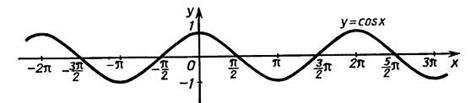Для продолжения графика по оси ОХ дальше, чем точка x=2π, необходимо воспользоваться свойством периодичности функции sin(x): sin(x+2πn)=sin(x), где n - целое число. Таким образом, график синуса на всей числовой прямой получается путем параллельного переноса его части на отрезке [0;2π] вдоль оси ОХ на 2π, 4π, 6π, и т.д.
График функции sin(x) называется синусоидой.

Задание 2. Построение графика функции у = cos(x)

Для построения графика функции cos(x) воспользуемся формулой приведения: cos(x)=sin(x+π/2). Следовательно, график функции косинуса получается из графика синуса путем его параллельного переноса на π/2 в отрицательном направлении оси абсцисс. График функции косинуса так же называется синусоидой.

Задание 3. Построение графика функции у = tg (x)

Построение графика тангенса производят с помощью линии тангенса и окружности аналогично построению синусоиды.

1. Начертить окружность произвольного радиуса (например 20 мм), прижав ее к левой стороне рисунка

2. Провести ось х через центр окружности и вертикальную линию ВС.

3. Провести линию тангенсов. (рис 1)

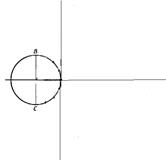
рисунок 1

4. Измерить радиус окружности и на оси х, от точки пересечения с ней окружности в правую часть отложить отрезок, равный 3R.

5. Разделить 1 и 4 четверти окружности на 4 равные части (поучится 8 частей), и отрезок на оси х на 8 равных частей.

6. Через середину отрезка провести ось у.

7. Выполнить разметку окружности и отрезка как показано на рис 2.

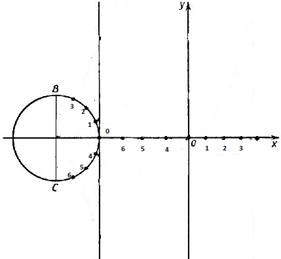
рисунок 2

4. Через точки деления окружности и центр окружности провести линии до пересечения с линией тангенсов, через точки пересечения провести горизонтальные линии.

5. Через точки деления отрезка АВ провести перпендикуляры и найти точки пересечения перпендикуляров с соответствующими горизонтальными линиями.

6. Соединить полученные точки линией – получим график функции у = tg (x) на промежутке (-π/2;π/2) (рисунок 3)

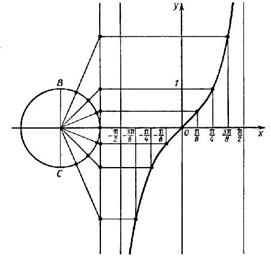
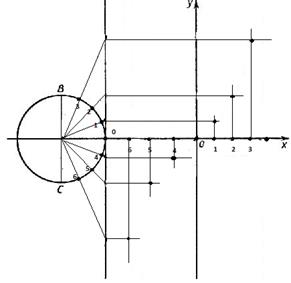
Выполняем построение графика функции у = tg х на всей числовой прямой.

Выполняем разметку:

на оси у 2 клеточки вверх 1, вниз -1

на оси х каждые 3 клеточки это одна четверть, получаем точки 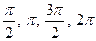и т.д

Так как для углов 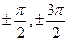и т.д. тангенс не определен, то проводим через эти точки пунктирные асимптоты.

Отмечаем вспомогательные точки 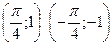, эти точки позволят построить график более точно. Проводим первую линию на интервале (-π/2;π/2). Вследствие тождества tg(x+πn)=tg(x), где n - целое, график функции тангенса на всей области определения получается из графика на интервале (-π/2;π/2) параллельными переносами вдоль оси ОХ вправо в влево на π 2π и т.д. График функции тангенс называют тангенсоидой. Получение графика путем параллельных переносов представлено на рисунке 4.

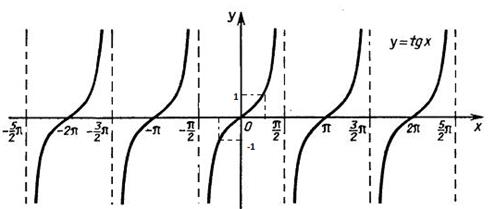
рисунок 4

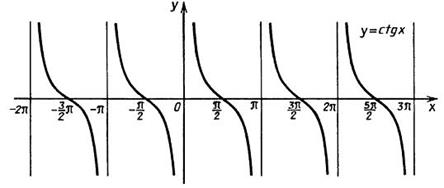
Задание 4. График функции котангенса можно получить из графика у = tg (x) путемотображения от оси Ох и сдвигом на p/2 вправо, так как ctg(x)= - tg (x+p/2) . Он представлен на рисунке ниже.

Задание 5. Заполните таблицу

Свойства тригонометрических функций (выпишите свойства функций на первом периоде)

Свойства	у = tg (x) на промежутке	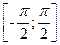у = сtg (x) на промежутке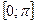
Область определения
Множество значений
Четность
Периодичность
Нули функции
y > 0
y < 0
Промежутки возрастания
Промежутки убывания
Максимумы
Минимумы