Лекция №2. Основные формулы комбинаторики. Теорема о перемножении шансов. Урны и шарики. Урновые схемы. Теорема о перемножении шансов. Доказательство теоремы 1.

Лекция №2

Основные формулы комбинаторики

Вопросы:

1.Теорема о перемножении шансов

2. Урны и шарики

3. Урновые схемы

В данном разделе мы займемся подсчетом числа «шансов». О числе шансов говорят, когда возможно несколько различных результатов какого-либо действия (извлечение карты из колоды, подбрасывание кубика или монетки, двух кубиков и т.д.). Число шансов — это число таких возможных результатов, или, иначе говоря, число способов проделать это действие.

1. Теорема о перемножении шансов

Теорема 1.

Пусть имеется, k групп элементов, причем i-я группа содержит n_i элементов, 1<=i<=k. Выберем из каждой группы по одному элементу. Тогда общее число N способов, которыми можно произвести такой выбор, равняется

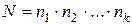
Замечание 1. В теореме 1 считается, что даже если все элементы в i-й группе неразличимы, выбрать один из них можно n_i способами.

Замечание 2.Результат выбора, описанного в теореме 1, представим в виде набора (а₁, а₂,…, а _k) в котором а_i — выбранный из i-й группы элемент. Тогда общее число различных наборов (а₁, а₂,…, а _k) также равняется

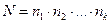
Доказательство теоремы 1.

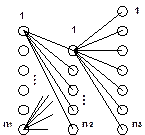Занумеруем элементы i -ой группы числами от 1 до n_i. Элемент из первой группы можно выбрать n₁способами. Если мы выбрали элемент j, 1<=i<= n₁, то выбрать элемент из второй группы мы можем n₂ способами. Получаем, что с первым элементом j возможно составить n₂ пар (j, l), где 1<=l<= n₂.

Но столько же пар можно составить и с любым другим элементом первой группы. Тогда всего пар, в которых первый элемент выбран из первой группы, а второй — из второй, существует ровно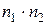

Иначе говоря, есть 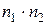способов выбрать по одному элементу из первых двух групп. Возьмем одну такую пару (j, l). Заметим, что элемент из третьей группы можно выбрать n₃ способами, то есть возможно составить ровно n₃ троек (j, l, m), добавляя к данной паре (j, l) любой из n₃элементов третьей группы.

Но столько же троек можно составить и с любой другой парой (j, l). Тогда всего троек, в которых первый элемент выбран из первой группы, второй — из второй, а третий — из третьей, существует ровно .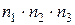

Продолжая рассуждения, методом математической индукции заключаем справедливость утверждения теоремы.

12 3 Следующая ⇒