а) движение навстречу друг другу, на сближение

⇐ ПредыдущаяСтр 2 из 2

М4М ч.2 с.10-11

Например, скорость автомобиля 70 км/ч, а скорость пешехода 5 км/ч и т.д.

В учебнике 4 кл. М.И. Моро есть специальная таблица примеров скоростей .

В процессе беседы вводят зависимости между величинами «скорость, время, расстояние»

· если известны расстояние (S) и время (t) движения, то можно найти скорость (v) действием деления; v=S:t

· если известны скорость (v) и время (t) движения, то можно найти расстояние (S)действием умножения; S=v*t

· если известны расстояние (S) и скорость (v), то можно найти время (t) движения действием деления t=S:v.

На этом этапе учим детей решать простые задачи на движение.

	скорость	время	расстояние
1 вид	5 км/ч	2 ч	?
2 вид	?	2 ч	10 км
3 вид	5 км/ч	?	10 км

Предлагая примеры таких задач, подбираем такие, чтобы в них использовались различные единицы измерения скорости: км/ч; м/с и т.д.

М4М ч.2 с.5-7.

Затем эту тройку величин включают в составные задачи, сначала нетиповые.

Например: туристы двигались 2 дня. В первый день они шли пешком 2 часа со скоростью 4 км/ч, а во второй день ехали на автобусе 30 км. Какое расстояние преодолели туристы за оба дня?

Затем эти величины включают в типовые задачи. Например, это может быть задача на нахождение 4 пропорционального или на пропорциональное деление или на нахождение неизвестного по двум разностям.

При решении простых задач на движение используется прием составления и решения обратных задач, это нужно для того чтобы учащиеся могли выявлять и использовать взаимно обратные связи между величинами, перестраивать суждения и умозаключения, использованные при решении прямой задачи. Обратные задачи – это продукт творчества учащегося, логическое продолжение прямой задачи. Составление и решение обратной задачи – один из путей саморазвития ученика.

Рассмотрим страницы учебников, в которых тема: «Задачи на движение» встречается впервые, сравним подготовительную работу, которую предлагают их авторы.

Истомина

По программе Истоминой задачи на скорость вводят в 4 классе во 2 части, детям предлагают формулировку задачи и затем рассуждение Миши и Маши по теме этой задачи.

М4И ч.2 с.38

На странице 39 автор предлагает определение скорости движения, берет его в рамочку, а также предлагает детям познакомится с единицами скорости.

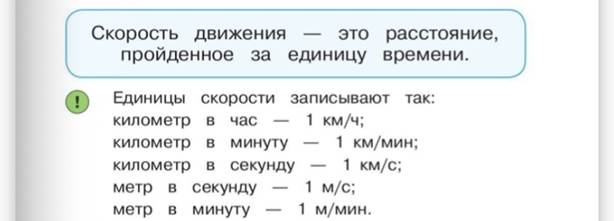
М4И ч.2 с.39

На страницах 41, 42, 44 автор знакомит детей с правилами как найти скорость, расстояние, время движения.

М4И ч.2 с.41

М4И ч.2 с.42

М4И ч.2 с.44

Дорофеев

По программе Дорофеева задачи на движение вводятся через таблицу, по которой детям нужно составить задачу самостоятельно, знания для этого у ребят уже есть, поэтому они справляются с данной задачей без затруднений.

М4Д ч.2 с.27

Петерсон

По программе Петерсон перед введением темы на движение автор проводит очень интересную и подробную подготовительную работу, на стр.65 дети узнают, как найти расстояние между двумя точками координатного луча, решают задачи на отработку нового правила.

М4П ч.2 с.65

Далее на стр.69 дети знакомятся с темой : «Движение по координатному лучу», автор предлагает большое количество интересных заданий, схем и картинок, которые помогают детям лучше разобраться и понять данную тему.

М4П ч.2 с.69

Вывод: самая интересная подготовительная работа представлена в учебниках Моро и Петерсон, авторы предлагают интересные задания, которые помогают подвести детей к теме, а также используют в своих учебниках картинки и схемы, по программе Истоминой подготовительная работа очень маленькая, зато все основные правила прописаны в учебнике и выделены в рамочку. В учебнике Дорофеева подготовительной работы нет вовсе, поэтому учителю придется подбирать задания и подводить детей к новой теме самостоятельно.

2. Составьте всевозможные простые и составные задачи на движение. М4М ч.2 с.10-11. Какова, по вашему мнению, цель урока, проводимого по этим страницам учебника? Опишите организацию деятельности учащихся при решении этих задач, используя приемы: выбор схемы, постановка или выбор вопроса к данному условию, условие с недостающими данными и др.

Цель урока: познакомиться со взаимосвязью величин: скорость, время, расстояние, формировать умения анализировать, составлять и решать задачи, совершенствовать вычислительные навыки, развивать пространственное воображение, образное мышление обучающихся, развивать логическое мышление, математическую речь учащихся, рассмотреть решение задач на движение, на нахождение пройденного пути с использованием формулы s=v*t, на нахождение затраченного времени с использованием формулы t=s:v.

Номер 1

Рассмотрите картинки на страницах 10 и 11, составьте по ним сначала простые, а затем составные задачи, в составлении задач используйте скорости, которые уже даны на страницах учебника.

· Турист был в пути 3 часа. Какой путь проделал турист, если он двигался со скоростью 5 км/ч?

· Всадник проехал 36 км со скоростью 12 км/ч . Сколько времени он был в пути?

· Лыжник, двигаясь со скоростью 4 м/с прошел весь путь длиной 800 м. Сколько времени он был в пути?

· Велосипедист двигался со скоростью 230 м/мин и проехал 2070 м. Сколько времени он был в путь?

· Мотоциклист был в пути 12 часов. Какой путь ему удалось преодолеть, если он двигался со скоростью 70 км/ч?

· Катя и ее сестренка Ира спускались с горки 9 минут. Какой путь они преодолели, если девочки шли со скоростью 35 м/мин?

· Красная машина двигалась со скоростью 80 км/ч, а синяя машина со скоростью на 25 км/ч больше. С какой скоростью двигалась синяя машина. На сколько скорость красной машины меньше скорости синей?

· Пассажирский поезд двигался со скоростью 120 км/ч . Это на 40 км/ч больше скорости товарного поезда. С какой скоростью двигался товарный поезд? На сколько скорость пассажирского поезда больше скорости товарного?

· Вертолет пролетает за 10 часов 2000 км со скоростью 200 км/ч, за сколько часов пролетит этот же вертолет это же расстояние со скоростью 250 км/ч?

· Байдарка плывет со скоростью 5 км/ч, катер со скоростью 35 км/ч , а яхта со скоростью 70 км/ч, за какое время каждое из плавающих средств проплывает расстояние 700 км?

Номер 2

· Пловец проплывает 100 м за 2 мин. Посмотрите на таблицу и подберите вопрос к данному условию. (С какой скоростью он плывет?)

· Бегун движется со скоростью 100м мин. Какое расстояние он преодолеет за … мин? Посмотрите на таблицу и вставьте в условие задачи пропущенные данные.

· Лыжник прошел дистанцию в 900 м за 5 мин. Найдите его скорость.

М4М ч.2 с.10

Номер 3

Составьте задачи, используя данные таблицы на странице 11.

· Катя прошла 36 км со скоростью 12 км/ч. Сколько времени она была в пути?

· Света была в пути 3 часа. Какое расстояние она преодолела, если ее скорость была 15 км/ч?

· За 2 часа Марина пробежала 6 км. С какой скоростью она двигалась?

М4М ч.2 с.11

3. Приведите примеры различных типовых и нетиповых составных задач на движение, которые представлены в различных учебниках математики для начальных классов. Могут ли задачи на движение в то же время быть задачами на нахождение 4-го пропорционального, на нахождение неизвестного по двум суммам или двум разностям? Приведите соответствующие примеры. Какие виды моделей наиболее эффективны при работе с такими задачами на движение? Приведите примеры разных моделей к задачам на движение.

В различных учебниках математики встречаются типовые и нетиповые составные задачи на движение, они могут быть в тоже время задачами на нахождение 4-го пропорционального, на нахождение неизвестного по двум суммам или двум разностям, к подобным задачам чаще всего удобнее применять таблицы нежели схемы, рассмотрим некоторые из них:

Задача на нахождение 4-го пропорционального:

М4Д ч.2 с.27

Задача на нахождение неизвестного по двум разностям:

М4М ч.2 с.41

Составная задача на движение:

М4П ч.2 с.79

4. Какую подготовительную работу необходимо провести прежде, чем познакомить учащихся с новым видом задач на движение – на движение в противоположных направлениях (на сближение и удаление друг от друга)? Приведите примеры таких заданий, подберите из учебников или придумайте самостоятельно, Какие методические приемы может использовать учитель при ознакомлении младших школьников с задачами на движение в противоположных направлениях? Какие новые понятия вводятся? Какие виды таких задач можно выделить?

Задачи на движение в разных направлениях – их два вида:

а) движение навстречу друг другу, на сближение

М4М ч.2 с.16

К задачам на движение можно делать таблицу. Но так же к каждой задаче можно сделать чертеж, т.е. схему со стрелками.

1 вид – на нахождение расстояния

7 км/ч 10 км/ч

3 ч 3 ч

? ?

1 способ:

1) 7 х 3=21 (км) расстояние, пройденное 1 лыжником.

2)10 х 3=30 (км) расстояние, пройденное 2 лыжником.

3) 21+30= 51 (км) общее расстояние.

2 способ: перед введением этого способа, вводят новое понятие – «скорость сближения». Чтобы детям был понятнее смысл этого понятия можно провести драматизацию ситуации. Обсуждаем, что за каждый час лыжники сближаются на расстояние, равное сумме скоростей каждого из них – это и называется скоростью сближения.

1) 7+10=17 (км/ч) скорость сближения

(т.е. на 17 км лыжники сближаются за каждый из 3-х часов)

2)17 ∙ 3=51(км) общее расстояние

К этой задаче рассматривают еще две обратные.

2 вид– на нахождение времени движения. М4М ч.2 с.16.

3 вид– на нахождение скорости одного из движущихся.М4М ч.2 с.16.

М4М ч.2 с.16

б) движение в противоположные стороны, на удаление.

М4М ч.2 с.33

? 7 км/ч 10 км/ч ?

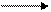
Аналогично предыдущему случаю разбирают .что такое скорость удаления – это расстояние, на которое удаляются движущиеся объекты за единицу времени. Она равна сумме скоростей.

Решают так же двумя способами.

1 способ 1) 7 ∙ 3=21(км) 2) 10 ∙ 3=30(км) 3) 30+21=51(км)

2 способ 1) 7+10=17(км/ч) – скорость удаления 2) 17 ∙ 3=51(км)

К такой задаче составляются две обратные, на нахождение времени и скорости.

М4М ч.2 с.33

По программе М.И. Моро кроме этих задач на движение других нет.

Но по программам Истоминой Н.Б. и АргинскойИ.И. разбирают задачи на движение в одном направлении.

Рассмотрим некоторые учебники, в которых встречаются темы на сближение и удаление друг от друга:

Чекин

На странице 46 автор знакомит детей с правилом : «При движении в противоположных направлениях скорость изменения расстояния между движущимися объектами равна сумме скоростей этих объектов»

М4Ч ч.2 с.46

На стр. 49 автор предлагает схемы, по которым нужно составить ситуацию, относящуюся к движению двух объектов, при этом нужно обратить внимание на исходное положение объектов, по схемам можно составить и задачи на сближение и задачи на удаление предметов друг от друга.

М4Ч ч.2 с.49

На стр.51 детям предлагается схема по которой нужно составить задачу на сближение, подобных заданий в данном учебнике очень много, они интересны детям, так как развивают мышление и воображение.

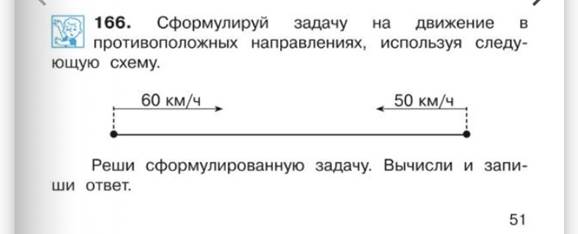
М4Ч ч.2 с.51

На стр.50 детям также предлагается составить задачу по схеме, но в этом случает уже получится задача на удаление.

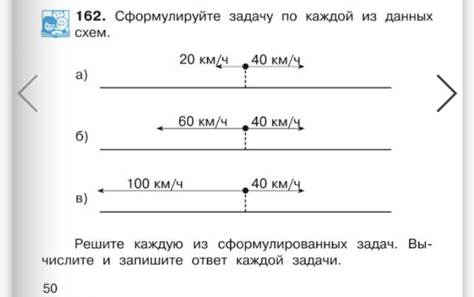
М4Ч ч.2 с.50

Истомина

По программе Истоминой детям предлагаются условия и схемы, которые нужно объединить, задание очень интересное, подобное можно встретить только в данном учебнике.

М4И ч.2 с.39

На стр.52 детям предлагают решить задачу на встречное движение, задача не сложная, автор также предлагает схему, которая поможет детям в их рассуждениях.

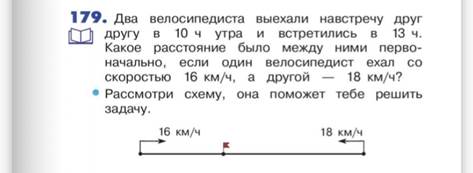
М4И ч.2 с.52

На стр.61 и 62 встречаются задачи на удаление, автор также предлагает схемы, которые помогают детям решить их.

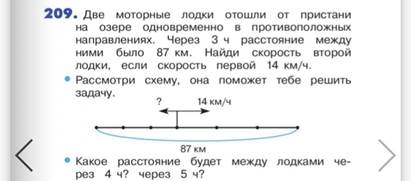
М4И ч.2 с.61

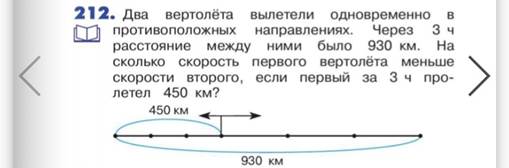
М4И ч.2 с.62

Петерсон

По программе Петерсон в 4 классе во 2 части детей знакомят с темой : «Одновременное движение по координатному лучу», рассматривается ситуация, в которой Незнайка и Кнопочка вышли одновременно навстречу друг другу.

М4П ч.2 с.77

На стр.78 предлагаются очень интересные задания на сближение и удаление предметов, подобные задания в других учебниках не встречаются.

М4П ч.2 с.78

На стр. 85 детям предлагают рисунки и схемы, по которым также нужно составить задачи на скорость сближение или скорость удаления.

М4П ч.2 с.85

На стр. 89 по программе Петерсон отдельно вводится тема : «Встречное движение», автор использует схемы и картинки, чтобы детям было более интересно и понятно изучать данную тему.

М4П ч.2 с.89

На стр. 90 автор предлагает составить по схемам задачи и решить их.

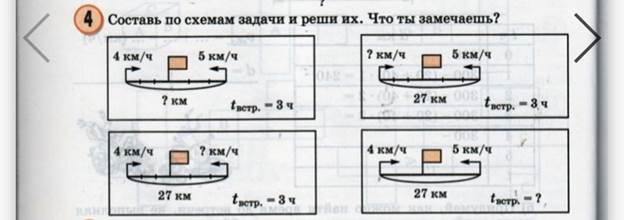
М4П ч.2 с.90

На стр.93 дети впервые знакомятся с темой: «Движение в противоположных направлениях», данной теме отводится целый урок, ее разбирают очень подробно.

М4П ч.2 с.93

На стр.94 мы видим примеры задач, которые использует автор для отработки темы: «Движение в противоположных направлениях».

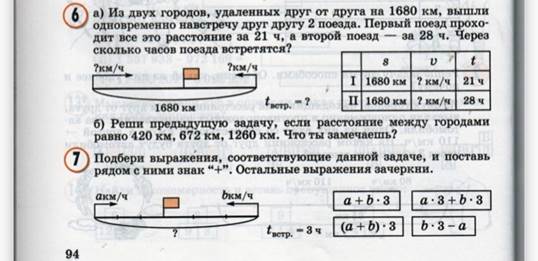
М4П ч.2 с.94

Вывод: в каждом из рассмотренных учебников авторы подробно знакомят детей с задачами на движение в противоположных направлениях (на сближение и удаление друг от друга), все учебники очень интересные и красочные, выделить какой-то один сложно.

Примеры собственных задач:

· Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

· Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

· Из стада одновременно в противоположных направлениях побежали два диких осла. Скорость одного 12 м/с, второго 8 м/с. Какое расстояние будет между ними через 8 мин?

⇐ Предыдущая 12