Хелпикс

Главная

Контакты

Случайная статья



Интегралы от иррациональных функций



Интегралы от иррациональных функций

Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те иррациональные функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, до конца интегрируются.

1) 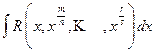, где R - рациональная функция своих аргументов (запись  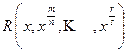указывает, что над величинами  производятся только рациональные операции).

Пусть k – общий знаменатель дробей 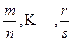. Сделаем подстановку:

.

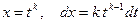Тогда каждая дробная степень x выразится через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию от t.

Пример:

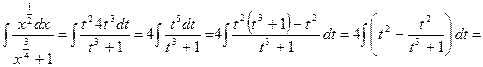
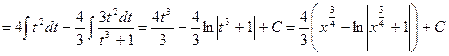
замена: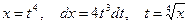

2)

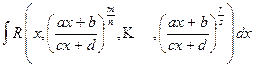
Этот интеграл сводится к интегралу от рациональной функции с помощью подстановки

,

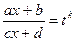где k - общий знаменатель дробей .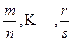

Пример:

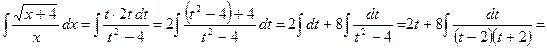
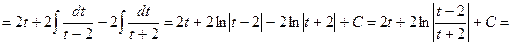
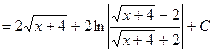
подстановка: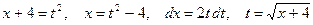

В ходе решения используем разложение дроби  на элементарные дроби:
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.