Домашняя контрольная по теории вероятностей

Домашняя контрольная по теории вероятностей

Задача 1. (на комбинаторику)

Вычислить число сочетаний из n по m (n и m выбираются по номеру варианта).

Задача 2.(на комбинаторику)

Вычислить число размещений из n по m. Во сколько раз полученный результат отличается от решения задачи 1. Ответ обосновать. (n и m выбираются по номеру варианта).

Задача 3. (на классическую вероятность)

А). Рассчитать лотерею Спортлото h из l. (h и l по номеру варианта)

Б). Код на кодовом замке состоит из d цифр от 0 до 9. Какова вероятность открыть этот замок с первого раза, если известно, что 1).цифры могут повторяться, 2).цифры не могут повторяться, 3). Сами цифры известны и различны, но неизвестен их порядок (d выбирается по номеру варианта).

В). Из 2 ящиков, содержащих шары с номерами от 1 до n выбирают по одному шару. Найти вероятность того, что сумма выбранных номеров будет меньше a, а произведение больше b.

Задача 4.(на геометрическую вероятность)

Решить задачу о встрече со следующими данными.

Интервал, в течении которого они могут прийти d минут

Первый ждёт u минут

Второй ждёт v минут

(d, u, v свои для каждого варианта)

Задача 5.(схема Бернулли)

Рассчитать вероятность получить

А).m успехов в n испытаниях Бернулли с вероятностью успеха p. В ответе досчитать всё до числа. (n, m, p свои для каждого варианта)

Б). число успехов в диапазоне [m1;m2]

Задача 6. (теоремы сложения, умножения верояностей)

1). Четыре стрелка делают по одному выстрелу по мишени. Вероятности попадания соответственно равны p1, p2,p3,p4. Найти вероятности событий A и B (содержание событий A и B и вероятности p1, p2, p3, p4свои для каждого варианта).

A={попал(и) только далее см. по номеру варианта}

B={начало см. по номеру варианта попадания(ий)}

2). Студент знает из вопросника к экзамену, состоящего из 40 вопросов q вопросов. Какова вероятность того, что он ответит на заданные ему один за другим подряд k вопросов из вопросника правильно, т.е. ему попадутся вопросы из тех, которые он знает.

Задача 7.

А). Дискретная с.в. X принимает значения от 1 до n. (т.е. 1, 2, 3 и т.д….n). вероятность для каждого значения 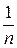. Записать распределение с.в. X в виде ряда. Найти математическое ожидание случайной величины X, дисперсию с.в. X и среднее квадратическое отклонение с.в. X, а также рассчитать для неё вероятность попасть в интервал [1,m] (n и m выбирается по номеру варианта).

Б).Из урны, содержащей 6 белых и 5 чёрных шаров выбирают случайным образом s шаров. Построить ряд распределения с.в. X – кол-ва белых (чёрных- в зависимости от варианта) среди отобранных. В ряду распределения всё можно оставить в терминах сочетаний. (s выбирается по номеру варианта, также по номеру варианта смотри какие шары рассматриваются чёрные или белые).

Задача 8.

Непрерывная с.в. Y задана своей плотностью

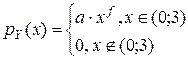
Найти постоянную a, математическое ожидание и дисперсию с.в. Y, среднеквадратическое отклонение с.в.Y и рассчитать вероятность её попадания в интервал (0;1). (f свое для каждого варианта).