
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Исследование систем линейных уравнений методом Гаусса.
Тема 1.2. Системы линейных уравнений.
§1. Исследование систем линейных уравнений. Метод Гаусса.
Пусть задана система из m линейных уравнений с n неизвестными x1, x2, …, xn:
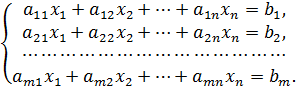 (*)
(*)
Если система имеет хотя бы одно решение, она называется совместной. Система, не имеющая ни одного решения, называется несовместной. Система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения.
Систему (*) можно записать в матричной форме: AX=B, где 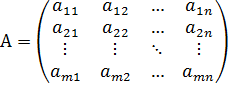 – матрица системы,
– матрица системы, 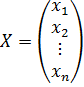 – столбец неизвестных,
– столбец неизвестных, 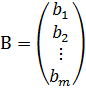 –столбец свободных членов.
–столбец свободных членов.
Матрица 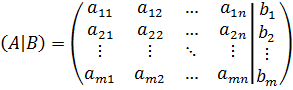 называется расширенной матрицей системы.
называется расширенной матрицей системы.
Теорема 2. 1. (Кронекера-Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы: r(A)=r( 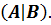
Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы – выяснить, определена она или нет. При этом возможны три варианта:
1) Если r(A)˂r(A|B), то система несовместна.
2) Если r(A)=r(A|B)=n (где n – число неизвестных), то система совместна и определена.
3) Если r(A)=r(A|B)˂n, то система совместна и неопределенна.
Исследование систем линейных уравнений методом Гаусса.
Задание №4 (пример).
А) Решить систему уравнений методом Гаусса: 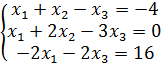
Решение. Приведём к ступенчатому виду расширенную матрицу системы: 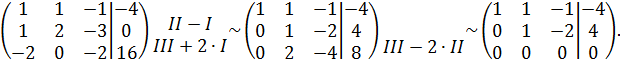
Так как r(A)=r(A|B)=2, n=3 ,согласно п. 3 (r(A)=r(A|B)˂n )система совместна и неопределенна (т. е. имеет бесконечно много решений).
Найдём общее решение системы и одно из частных решений системы.
Количество главных переменных равно r(A)=2, количество свободных переменных равно n‒ r(A)=3‒2=1. Выберем какой-нибудь не равный нулю минор 2-го порядка полученной матрицы А, например, минор 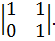 Его столбцы – 1-й и 2-й столбцы матрицы А – соответствуют переменным x1 и x2 – это будут главные переменные, а x3 – свободная переменная. Запишем систему уравнений, соответствующую полученной расширенной матрице:
Его столбцы – 1-й и 2-й столбцы матрицы А – соответствуют переменным x1 и x2 – это будут главные переменные, а x3 – свободная переменная. Запишем систему уравнений, соответствующую полученной расширенной матрице: 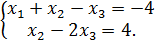
Теперь для наглядности запишем эту систему в другом виде (слева остаются только главные переменные): 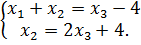
Подставляя выражение для x2 в первое уравнение, получим x1=‒x3‒8. Обозначая свободную переменную x3 через t, получим общее решение системы:
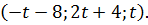 Частное решение системы получим, например, при t=0: (‒8; 4; 0).
Частное решение системы получим, например, при t=0: (‒8; 4; 0).
Ответ. Система совместна и неопределенна; общее решение 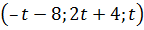 ; частное решение (‒8; 4; 0).
; частное решение (‒8; 4; 0).
Б) Решить систему уравнений методом Гаусса: 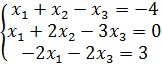
Решение. Приведём к ступенчатому виду расширенную матрицу системы: 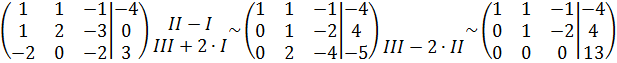 . Так как r(A)=2, а r(A|B)=3, то согласно п. 1( r(A)˂r(A|B)) система несовместна.
. Так как r(A)=2, а r(A|B)=3, то согласно п. 1( r(A)˂r(A|B)) система несовместна.
Ответ. Система несовместна.
В) Решить систему уравнений методом Гаусса: 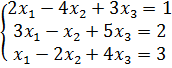 .
.
Решение. Приведём к ступенчатому виду расширенную матрицу системы: 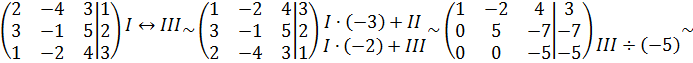
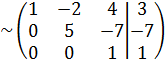 .
.
Так как r(A)=r(A|B)=3, n=3 ,согласно п. 2 (r(A)=r(A|B)=n )система совместна и определена. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице: 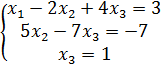 . Решим эту систему:
. Решим эту систему: 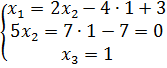 ;
; 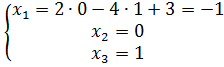 .
.
Ответ. Система совместна и определена; общее решение (‒1;0;1); частное решение (‒1;0;1).
§2. Решение систем линейных уравнений с помощью обратной матрицы и по методу Крамера.
Пусть система из n линейных уравнений с n неизвестными задана в матричной форме: AX=B, где A=(aij) – матрица коэффициентов системы размера n×n, 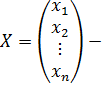 столбец неизвестных,
столбец неизвестных, 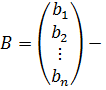 столбец свободных членов.
столбец свободных членов.
Если D – определитель матрицы А – не равен нулю, то система совместна и определена, её решение задаётся формулой: 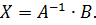
Другую форму записи этого утверждения дают формулы Крамера:
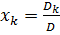 , k=1, 2, …, n, где Dk – определитель, получающийся из D заменой k-го столбца на столбец свободных членов.
, k=1, 2, …, n, где Dk – определитель, получающийся из D заменой k-го столбца на столбец свободных членов.
Задание №3 (пример). Решить систему уравнений по формулам Крамера и с помощью обратной матрицы: 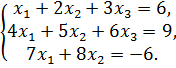
Решение.
а) Решим систему по формулам Крамера. Для этого найдём определитель матрицы системы: 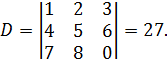 Так как D≠0, то система совместна и определена. Найдём определители D1, D2, D3 подставляя столбец свободных членов
Так как D≠0, то система совместна и определена. Найдём определители D1, D2, D3 подставляя столбец свободных членов 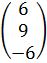 вместо первого, второго и третьего столбцов определителя D соответственно:
вместо первого, второго и третьего столбцов определителя D соответственно:
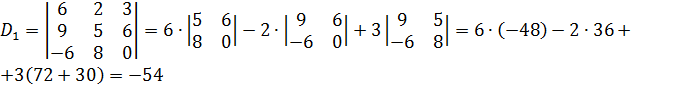 ,
,
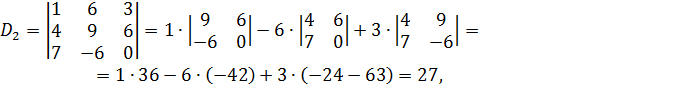
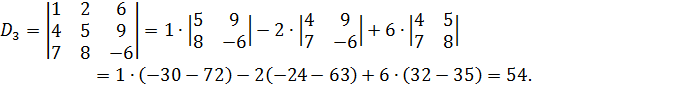
Отсюда получаем решение системы уравнений:
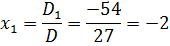
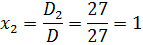
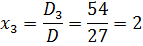
Ответ. ( ̶ 2; 1; 2).
Б) Решим систему с помощью обратной матрицы. Найдём матрицу А ̶ 1, обратную к матрице системы 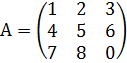 . Эта матрица найдена в примере№ 5:
. Эта матрица найдена в примере№ 5: 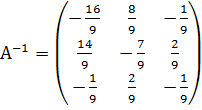 . Найдём решение системы уравнений:
. Найдём решение системы уравнений:
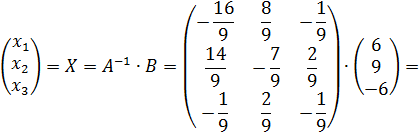 =
= 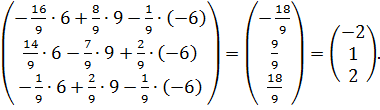
Ответ. 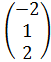 .
.
Практические задания
1. Решить систему уравнений по формулам Крамера и методом обратной матрицы:
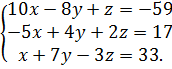
2. Исследовать систему линейных уравнений методом Гаусса:
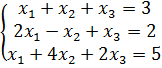
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|