Хелпикс

Главная

Контакты

Случайная статья



Учебник №240(1,3), 241(1), 242(1), 244(1). Выполнить самостоятельно.



 

4.12.2020 10 класс математика

1 Смотреть https://youtu.be/iO1ZM2J4IMY - решение систем показательных уравнений и систем показательных неравенств.

2. Отметим, что при решении систем показательных уравнений и неравенств, применяются те же приемы, что при решении систем алгебраических уравнений и неравенств (метод подстановки, метод сложения, метод введения новых переменных). Во многих случаях, прежде чем применить тот или иной метод решения, следует преобразовать каждое уравнение (неравенство) системы к возможно более простому виду.

 

3. Обратим внимание, что при решении неравенств следует помнить, что показательная функция y = аx возрастает при а˃1 и убывает при 0˂ а˂1. Значит, в случае, когда равны основания степени, следует переходить к неравенству показателей, учитывая возрастание(убывание) функции.

 

4. Примеры

Пример 1:

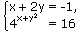
Решение: Решим эту систему способом подстановки:

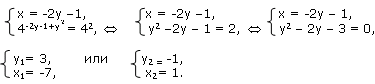
Ответ: (-7; 3); (1; -1).

Пример 2:

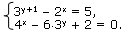
Решение: Обозначим 2х= u, 3y = v. Тогда система запишется так:

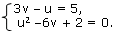
Решим эту систему способом подстановки:

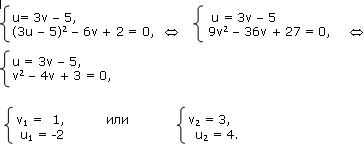
a)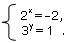

Уравнение 2х = -2 решений не имеет, т.к. –2 <0, а 2х > 0.

b)

Ответ: (2;1).

Пример 3:

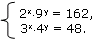
Решение: Перемножим уравнения данной системы. Получим

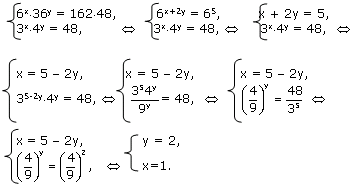
Ответ: (1;2).

Пример 4:

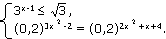
Решение:1) Решим неравенство


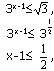
т.к. функция у=3t возрастает,

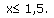
2) Решим уравнение

(0,2)3x2 -2=(0,2)2х2+х+4,

3х2– 2 = 2х2 +х + 4,

х2– х – 6 = 0,

х1 = 2> 1,5;

х2= -3 < 1,5; следовательно х = -3.

Ответ:-3.

 

5.Учебник №240(1,3), 241(1), 242(1), 244(1). Выполнить самостоятельно.

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.