Тема : Способы задания функции. График функции.

Задание для группы 109 з на 23.11 2020

Тема : Способы задания функции. График функции.

Задание 1 :Законспектировать ( стр 159-161)

Учебник В.Т. Лисичкин, И. Л. Соловейчик Математика в задачах с решениями.

Задание 2: Построить графики функций: y = x +1; y = - 1/x ; y = x²- 4;

y = |2x + 3|; y = |x² -1|

Ответы высылать на почту tuzkova54@bk.ru или вайбер( вацап) 89051310056

Задание для группы 109 з на 24.11 2020

Тема : Основные свойства функции

К основным свойствам функции относится монотонность, четность, периодичность, обратимость.

Функция монотонна на интервале, если она на интервале или только убывает или только возрастает.

Функция y = f (x) называется возрастающей на интервале, если для любых x из этого интервала большему значению аргумента соответствует большее значение функции. Т.е. при x₁< x ₂имеет место неравенство

f (x₁) < f (x₂).

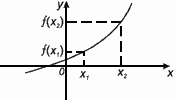
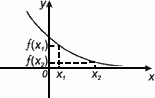
Функция y = f (x) называется убывающей на интервале, если для любых x из этого интервала большему значению аргумента соответствует меньшее значение функции. Т.е. при x₁< x ₂имеет место неравенство

f (x₁) >f (x₂).

Например определим монотонность функции y = 2 – x на отрезке [-5; 6]

В этом случаи x₁ = -5 , x₂ = 6, x₁ < x₂ . Найдем y( -5) = 2 – (-5) = 7,

y(6) = 2- 6 = -4. Получается y ₁ > y _2.Следовательно функция убывает.

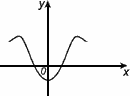
Функция y = f (x) называется чётной, если для любого аргумента x из области определения функции выполняется условие f (-x) = f (x).

Функция y = f (x) называется нечётной, если для любого аргумента x из области определения функции выполняется условие f (-x) = - f (x).

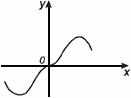
График чётной функции симметричен относительно ординат, а график нечётной функции симметричен относительно начала координат.

Если условие чётности и нечётности не выполняется, то функция называется функцией общего вида.

Определим чётность функции y = x³ +x. y (- x) = (- x)³ + (-x) = - x³ - x = -( x³ +x),т.е. y( -x) = - y( x). Значит функция нечётная.

Функция f(x) называется периодической с периодом 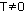, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

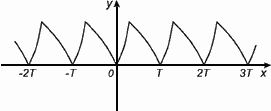
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

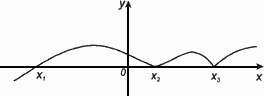
Х₁,Х₂,Х₃ – нули функции y = f(x).

Пусть функция y = f(x) определена на отрезке [a;b] и является монотонной, а область значений функции y есть отрезок [c;d]. Каждому значению y₀ из отрезка [c;d] будет соответствовать одно значение x₀ из отрезка [a;b] такое , что y₀ = f (x₀). Следовательно , на отрезке[c; d] определена функция x =φ(y). Эта функция x =φ(y) называется обратной для функции y = f(x) и , наоборот, функция y = f(x) является обратной для функции x =φ(y). Их называют взаимно обратными. Графики обратных функций симметричны относительно прямой y = x

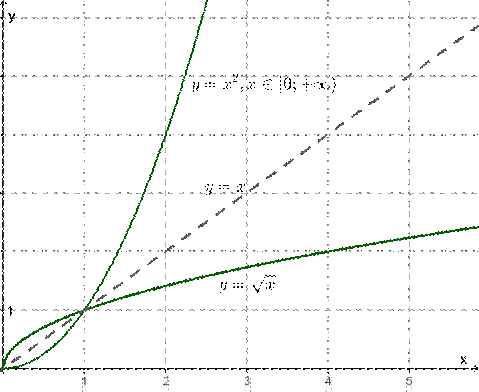
Дана функция y=x²,x∈[0;+∞). Найти обратную функцию.

Заданная функция возрастает на промежутке [0;+∞), значит, она имеет обратную функцию. Из уравнения y=x² находим: x=√y . Промежутку [0;+∞) принадлежат лишь значения функции x=√y. Это и есть обратная функция, которая определена на промежутке [0;+∞).

Поменяв местами x и y, получим: y=√x∈[0;+∞). График этой функции получается из графика функции y=x²,x∈[0;+∞) с помощью симметрии относительно прямой y=x.

Задание

1. Определите монотонность функций y = x² +1 на [-5;-2]; y = x³ на [-1; 3]; y = - 2/x на [1; 4]

2. Определите чётность функций y = x² -x; y = 1/x; y = 2x; y = x² +5

3. Найти функцию, обратную данной y = x -3; y = (x -2)³