Хелпикс

Главная

Контакты

Случайная статья



ИНСТРУКЦИОННАЯ КАРТА. по дисциплине: «МАТЕМАТИКА»



ИНСТРУКЦИОННАЯ КАРТА

по дисциплине: «МАТЕМАТИКА»

Тема:                     Предел функции. Непрерывность функции.

Цель:                     Закрепить понятия: предел функции, непрерывность функции в точке; пояснить важность нахождения предела функции для исследования ее на непрерывность; научиться находить пределы, используя основные теоремы о пределах, раскрывать неопределенности типа 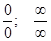 и использовать замечательные пределы.

 

Методические рекомендации по выполнению практического задания:

  1. .Знать определение предела функции, теоремы о пределах, замечательные пределы, определение непрерывной в точке и на промежутке функции.
  2. Ознакомиться с материалами практического задания.

 

Ход работы:

№ 1 Найти:

1. значение функции 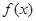 в точке 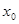, т.е. ;

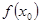2. предел функци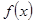и  при, 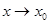, т.е. ;

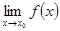3. если 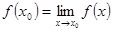, то 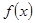 непрерывна в точке 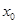, если же нет, то  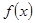терпит разрыв в точке .

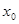Доказать непрерывность функции в указанной точке:


1)

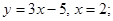
2)


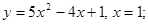
3)

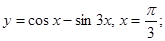
4)


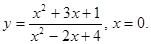
№ 2 Т.к. функции в указанных точках непрерывны, для нахождения предела достаточно найти значение функции в точке.

Найти предел функции:


1) ;


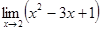2) ;


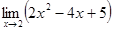3) .


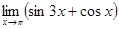№ 3 Имеем неопределенность вида 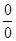. Чтобы избавиться от неопределенности, нужно числитель и знаменатель разложит на множители и сократить дробь.

Найти предел функции:


1) ;

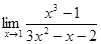2) ;

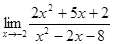3) ;

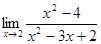4)


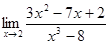
№ 4 Для вычисления предела в случае неопределенности вида 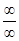 при 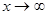 числитель и знаменатель дроби необходимо поделить на старшую степень переменной. При этом , если многочлены в числителе и в знаменателе одной степени, то предел равен отношению коэффициентов при старших степенях; если разных степеней; то предел равен 0 или 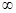(учитываем, что ).

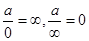Найти предел функции:


1) ;

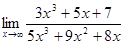2) ;


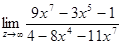3) ;

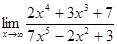4) .


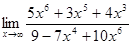№ 5 Чтобы избавиться от неопределенности вида 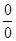 в случае иррациональности (выражение содержит радикал) в числителе или знаменателе, надо и числитель, и знаменатель умножить на выражение, сопряженное иррациональности, упростить и сократить дробь (a-b и a+b – сопряженные выражения; (a-b)(a+b)=a2-b2 ; ).

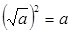Найти предел функции:


1)

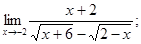
2)

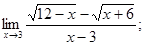
3)

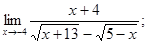
4)

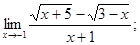
5)


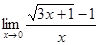
№ 6 Использовать 1-й замечательный предел и следствие из него:

;    .

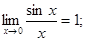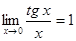Найти предел функции:


1)

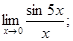
2)


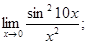
3)

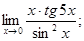
4)


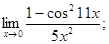
5)

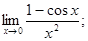
6) .


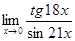№ 7 Использовать 2-й замечательный предел и следствие из него:

; ;   .

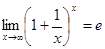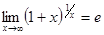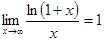Найти предел функции:


1)

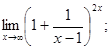
2)

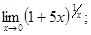
3)

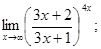
4)


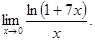
После практической работы студент должен:

Знать:

¾ Определение предела функции, непрерывности функции в точке, правила вычисления пределов.

Уметь:

¾ Находить пределы функций, используя различные методы и правила; выяснять, является ли данная функция непрерывной в данной точке.

Преподаватель                                                                     Кононова М.П.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.