Число е. Замечательные пределы.

Дата	30.09.2020 г.
Специальность	1304000, «Вычислительная техника и программное обеспечение (по видам)»
Группа	ВТ-21
Предмет	Основы высшей и дискретной математики
Тема	Число е. Замечательные пределы. Лекция.

Ссылка:

https://www.youtube.com/watch?v=VQEB4fZ0kx8&ab_channel=%D0%92%D0%B8%D0%B4%D0%B5%D0%BE%D0%BA%D1%83%D1%80%D1%81%D1%8BDAVINCI

Число е. Замечательные пределы.

Лекция

В курсе математического анализа, доказывается, что:

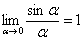
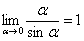– тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра 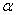может выступать не только переменная 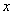, но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Примеры:
, , ,

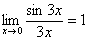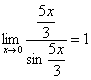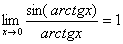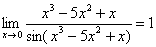
Здесь 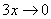, , , , 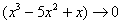первый замечательный предел применим.

Пример 1

Найти предел

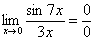
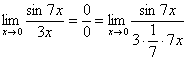
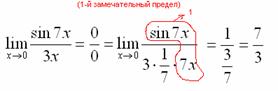
Пример 2

Найти предел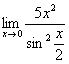

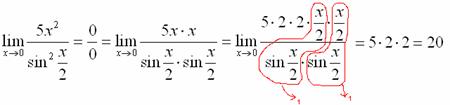
Пример 3

Найти предел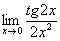

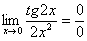
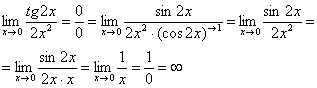
Пример 4

Найти предел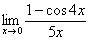

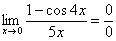
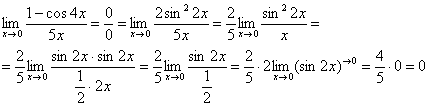
Второй замечательный предел

В теории математического анализа доказано, что:

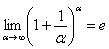
Данный факт носит название второго замечательного предела.

Справка: 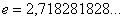– это иррациональное число.

В качестве параметра 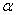может выступать не только переменная 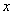, но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел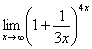

Пример 7

Найти предел

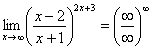
второй замечательный предел выглядит следующим образом: 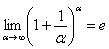. Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:

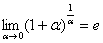
Пример 8

Найти предел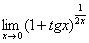

Итог занятия.

Домашнее задание:конспект, Богомолов Н. В стр82

Литература:

Богомолов И.В. «Практические занятия по высшей математике» Москва 2010г.

Ссылка:

https://www.youtube.com/watch?v=VQEB4fZ0kx8&ab_channel=%D0%92%D0%B8%D0%B4%D0%B5%D0%BE%D0%BA%D1%83%D1%80%D1%81%D1%8BDAVINCI