Вопросы ко второй аттестации по разделам

Вопросы ко второй аттестации по разделам

«Двойные и несобственные интегралы.

Числовые и степенные ряды. Ряды Фурье »

I курс, 2 семестр, 2010 – 2011 учебный год, для студентов института САУ

1. Понятие двойного интеграла. Геометрический смысл двойного интеграла.

2. Свойства двойных интегралов.

3. Сведение двойного интеграла к повторному. Зависимость порядка интегрирования от вида области (2 случая).

4. Переход в двойном интеграле к полярным координатам. Сведение двойного интеграла к повторному в полярных координатах.

5. Понятие несобственного интеграла на бесконечном промежутке.

6. Сходимость несобственного интеграла 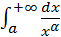в зависимости от α.

7. Признаки сходимости несобственных интегралов от неотрицательных функций.

8. Понятие абсолютной и условной сходимости несобственных интегралов.

9. Понятие числового ряда. Частичные суммы. Сходимость и расходимость числового ряда.

10. Понятие числового ряда. Необходимое условие сходимости числового ряда.

11. Свойства сходящихся числовых рядов: сложение (вычитание), умножение на число.

12. Критерий Коши сходимости числового ряда. Гармонический ряд.

13. Интегральный признак сходимости числовых рядов с неотрицательными членами. Сходимость ряда 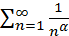в зависимости от α.

14. Признаки сходимости числовых рядов с неотрицательными членами: признак сравнения, предельный признак сравнения.

15. Признаки сходимости числовых рядов с неотрицательными членами: признак Даламбера, признак Коши.

16. Знакочередующиеся числовые ряды. Признак Лейбница.

17. Абсолютная и условная сходимость числовых рядов.

18. Понятия функциональной последовательности и функционального ряда, их сходимость в точке и на множестве.

19. Определения равномерной сходимости функциональной последовательности и функционального ряда.

20. Понятие степенного ряда. Теорема Абеля.

21. Интервал и радиус сходимости степенного ряда.

22. Формулы для вычисления радиуса сходимости степенного ряда (из признаков Даламбера и Коши).

23. Свойства степенных рядов.

24. Формулы Тейлора и Маклорена с остаточным членом в форме Пеано. Ряды Тейлора и Маклорена.

25. Разложение в ряд Маклорена функций: ,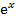

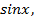
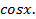
26. Разложение в ряд Маклорена функций: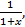

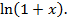
27. Разложение в ряд Маклорена функций: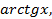

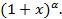
28. Ряд и коэффициенты Фурье для периодических функций с периодом .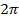

29. Ряд и коэффициенты Фурье для периодических функций с периодом .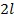

30. Ряд и коэффициенты Фурье для четных и нечетных функций.

Лекторы

кандидат физ.-мат. наук, доцент Е. В. Арбузова

кандидат физ.-мат. наук, доцент Т. В. Копылова