Вопросы к первой аттестации по разделам

Вопросы к первой аттестации по разделам

«Элементы теории функций комплексной переменной.

Неопределенный и определенный интегралы»

I курс, 2 семестр, 2010 – 2011 учебный год, для студентов института САУ

1. Определение комплексного числа, действительная и мнимая части комплексного числа. Алгебраическая форма записи комплексного числа. Комплексно сопряженные числа, произведение .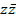

2. Комплексная плоскость, геометрическое изображение комплексных чисел. Модуль и аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.

3. Комплексная плоскость, геометрическое изображение комплексных чисел. Модуль и аргумент комплексного числа. Показательная форма записи комплексного числа.

4. Формула Эйлера. Показательная форма записи комплексного числа. Возведение комплексного числа в степень 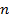. Извлечение корня 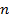-й степени из комплексного числа.

5. Показательная функция комплексной переменной 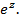Выражение тригонометрических функций 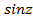, 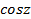и гиперболических функций через показательную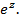

6. Показательная функция комплексной переменной 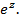Выражения для логарифмической, общей степенной и общей показательной функций.

7. Определение производной функции комплексной переменной. Действительная и мнимая части функции комплексной переменной. Условия Коши-Римана.

8. Понятие первообразной функции, свойства первообразных. Определение неопределенного интеграла.

9. Понятие первообразной функции. Неопределенный интеграл и его свойства.

10. Таблица основных неопределенных интегралов (14 интегралов).

11. Формула замены переменной в неопределенном интеграле. Формула интегрирования по частям в неопределенном интеграле.

12. Интегральная сумма Римана, определенный интеграл и его геометрический смысл.

13. Основные свойства определенного интеграла.

14. Оценки определенных интегралов. Теорема о среднем, формула среднего значения.

15. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

16. Формула замены переменной в определенном интеграле. Формула интегрирования по частям в определенном интеграле.

17. Интегральная сумма Римана. Формулы для вычисления площади криволинейной трапеции в прямоугольных декартовых координатах и площади криволинейного сектора в полярной системе координат.

18. Формулы для вычисления длины дуги плоской кривой в прямоугольных декартовых координатах. Дифференциал дуги плоской кривой и его геометрический смысл.

Лекторы

кандидат физ.-мат. наук, доцент Е. В. Арбузова

кандидат физ.-мат. наук, доцент Т. В. Копылова