Хелпикс

Главная

Контакты

Случайная статья



Тема: Обратные тригонометрические функции



Тема: Обратные тригонометрические функции

Актуализация знаний

Вопросы :

- какие функции вы уже знаете?

- дайте определения тригонометрическим функциям;

 Работа по таблице на стр. 6:

- синус какого угла равен ; ; ?

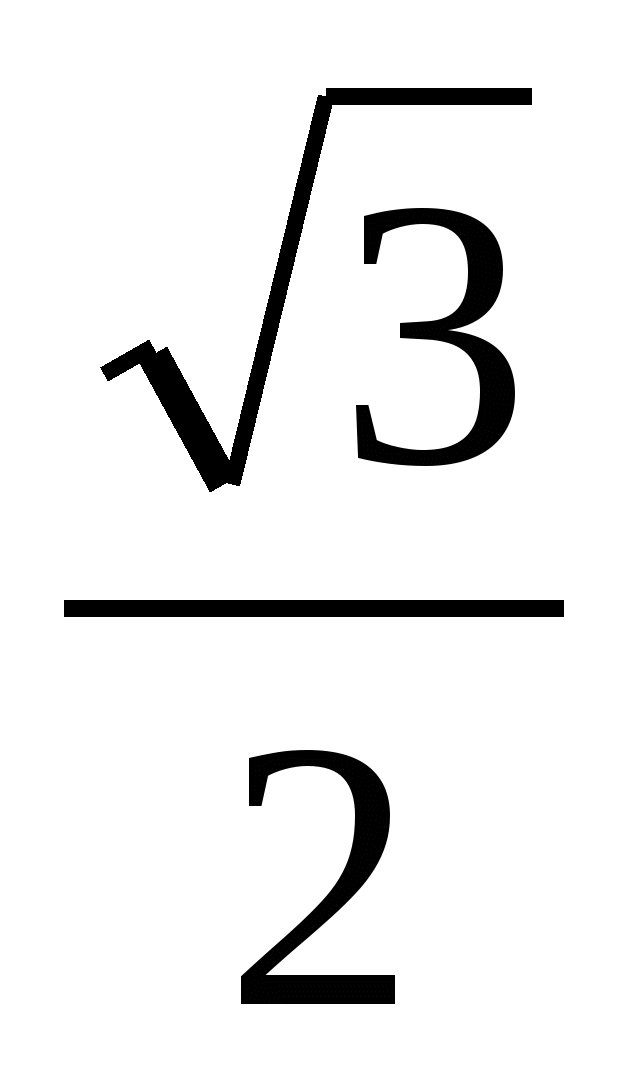- найдите значения ; ; ; .

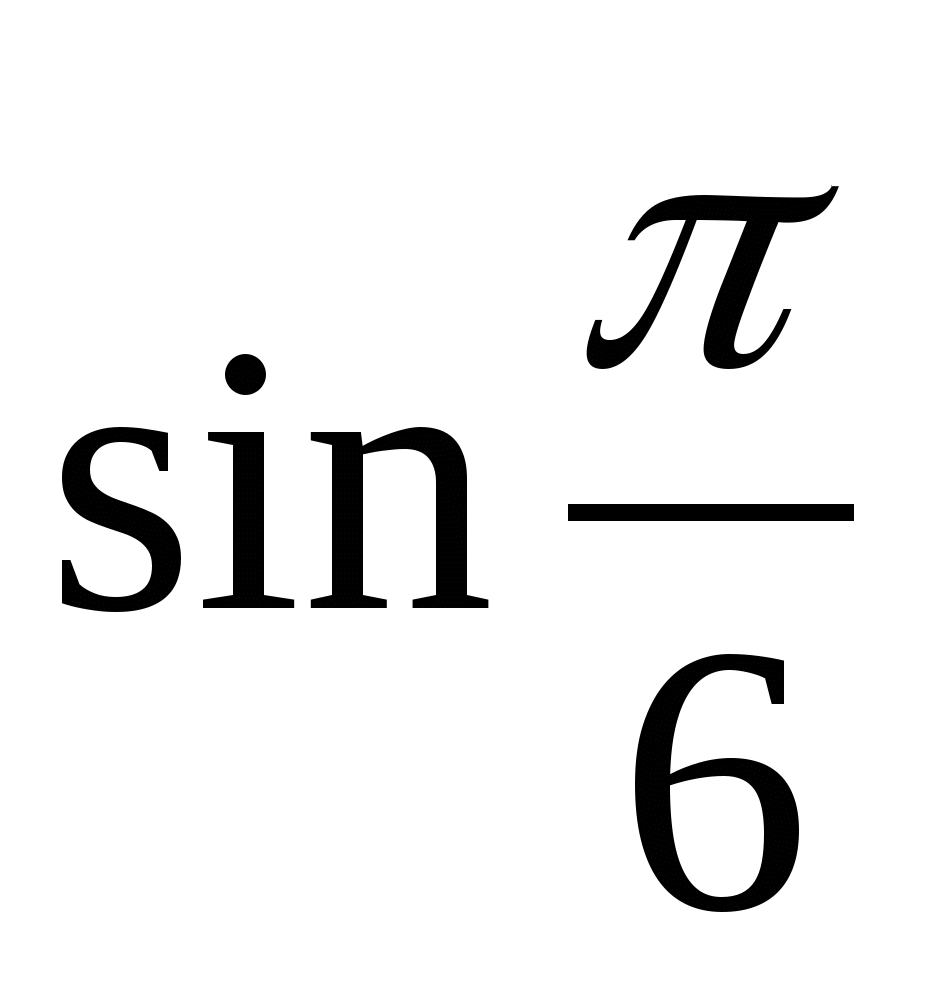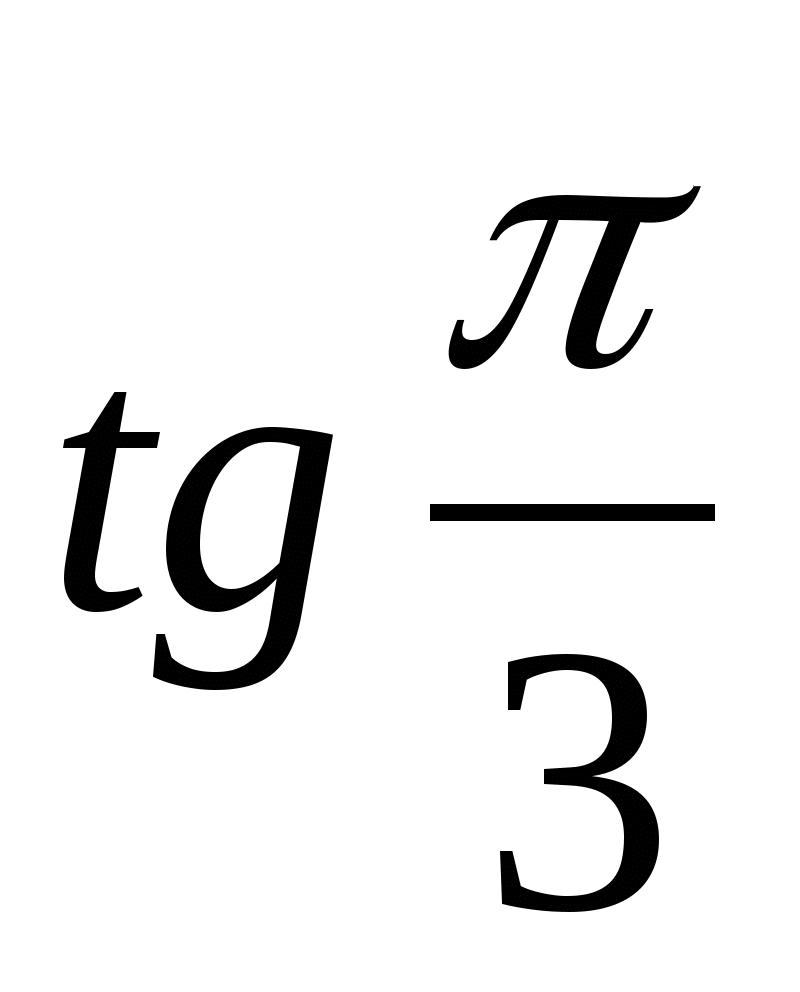Работа над новым материалом

Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью.

 

1.Арксинус. Определение.

Арксинусом числа α называется такое число из отрезка 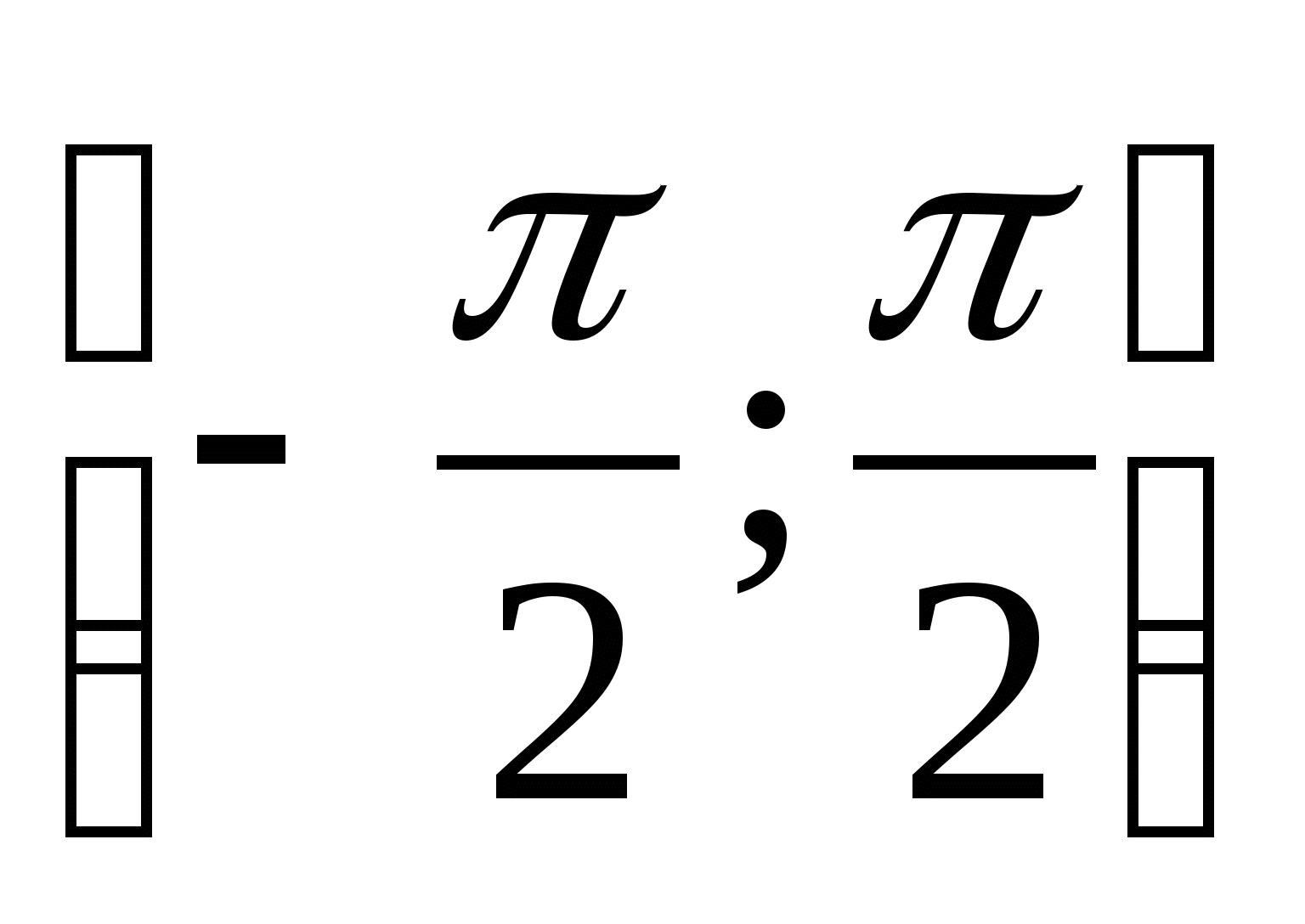, синус которого равен α. Арксинус является нечетной функцией, то есть:

                                                                               

 

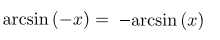
Пример 1. Вычислите: а) ; б) .

 

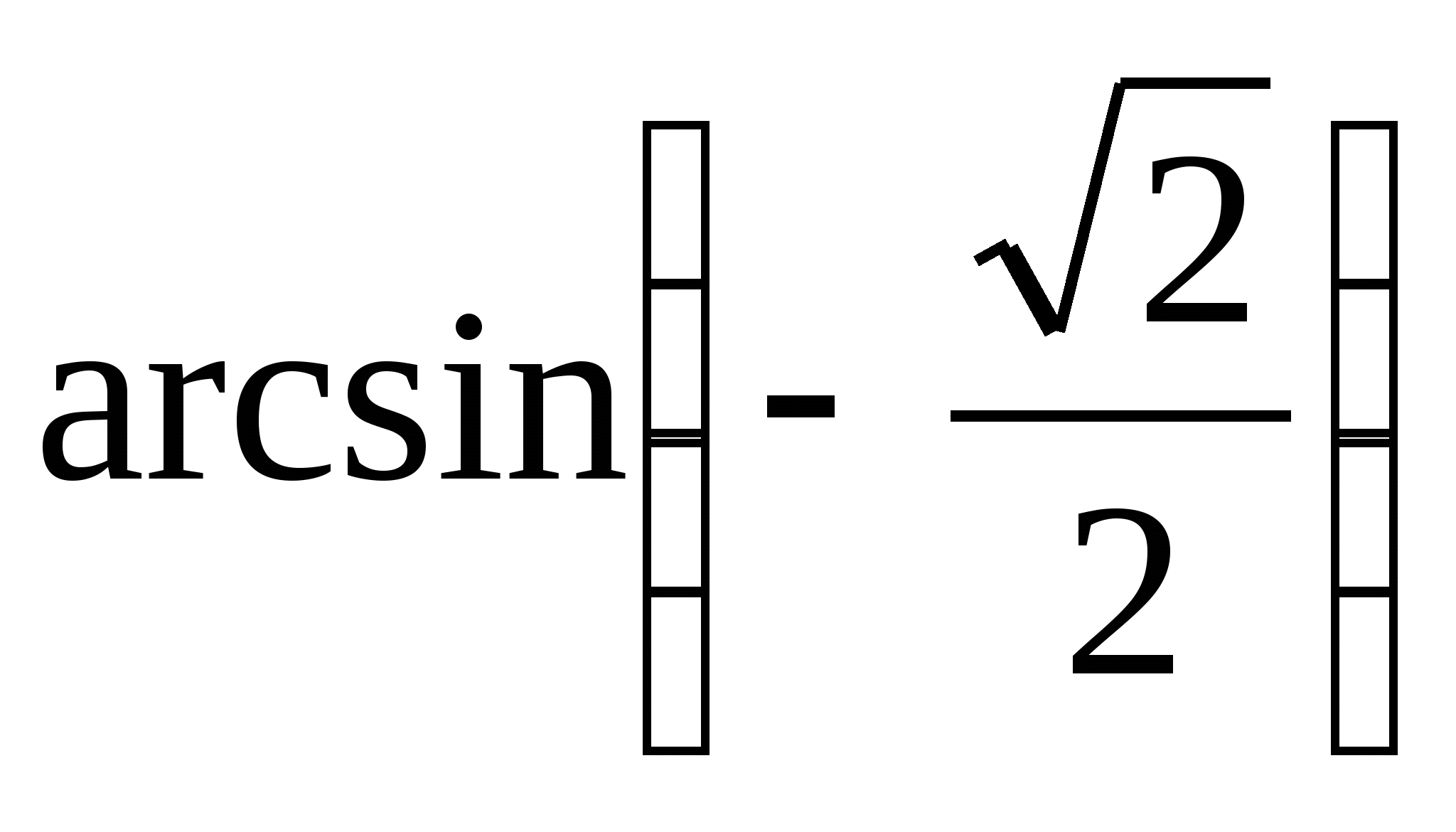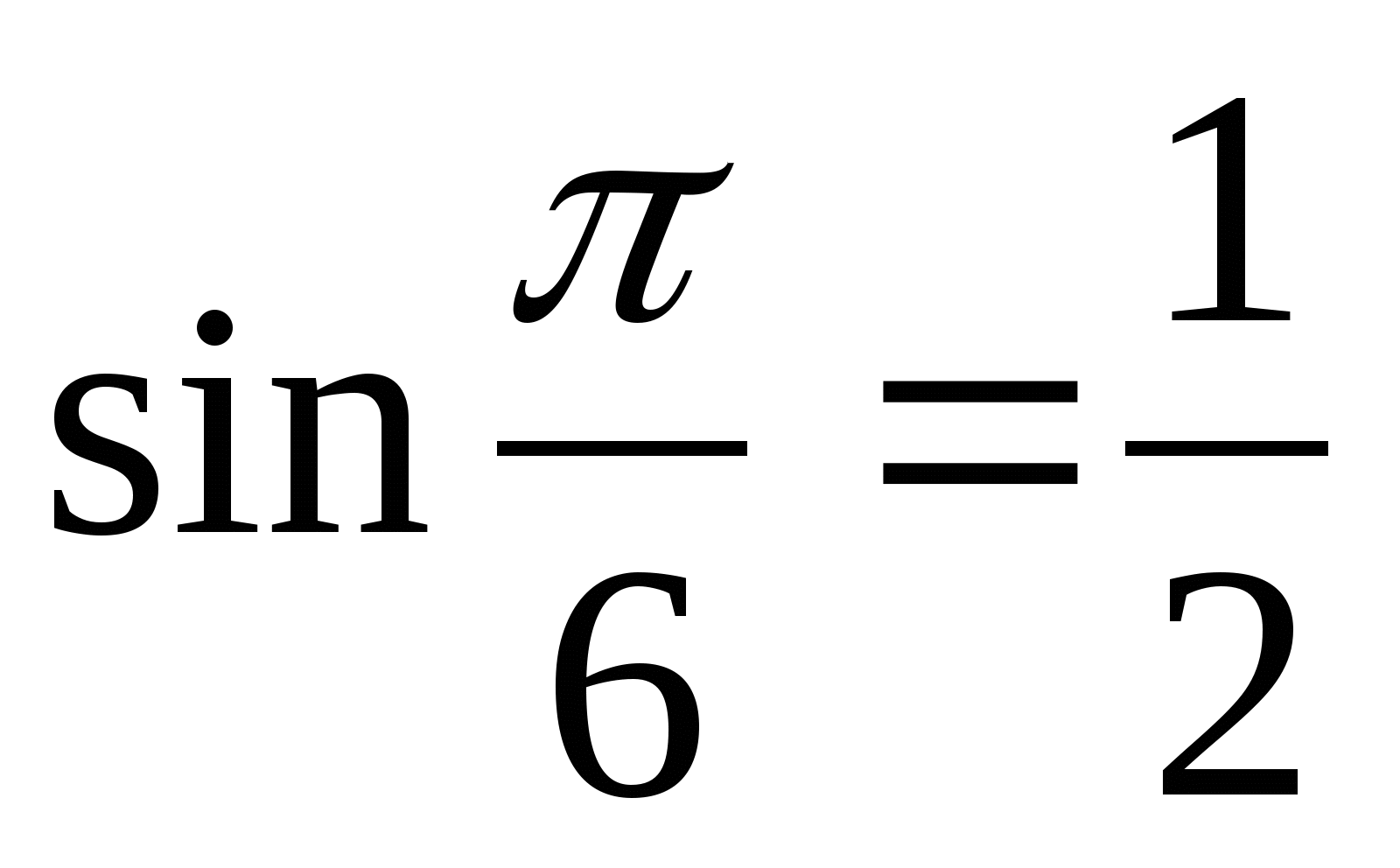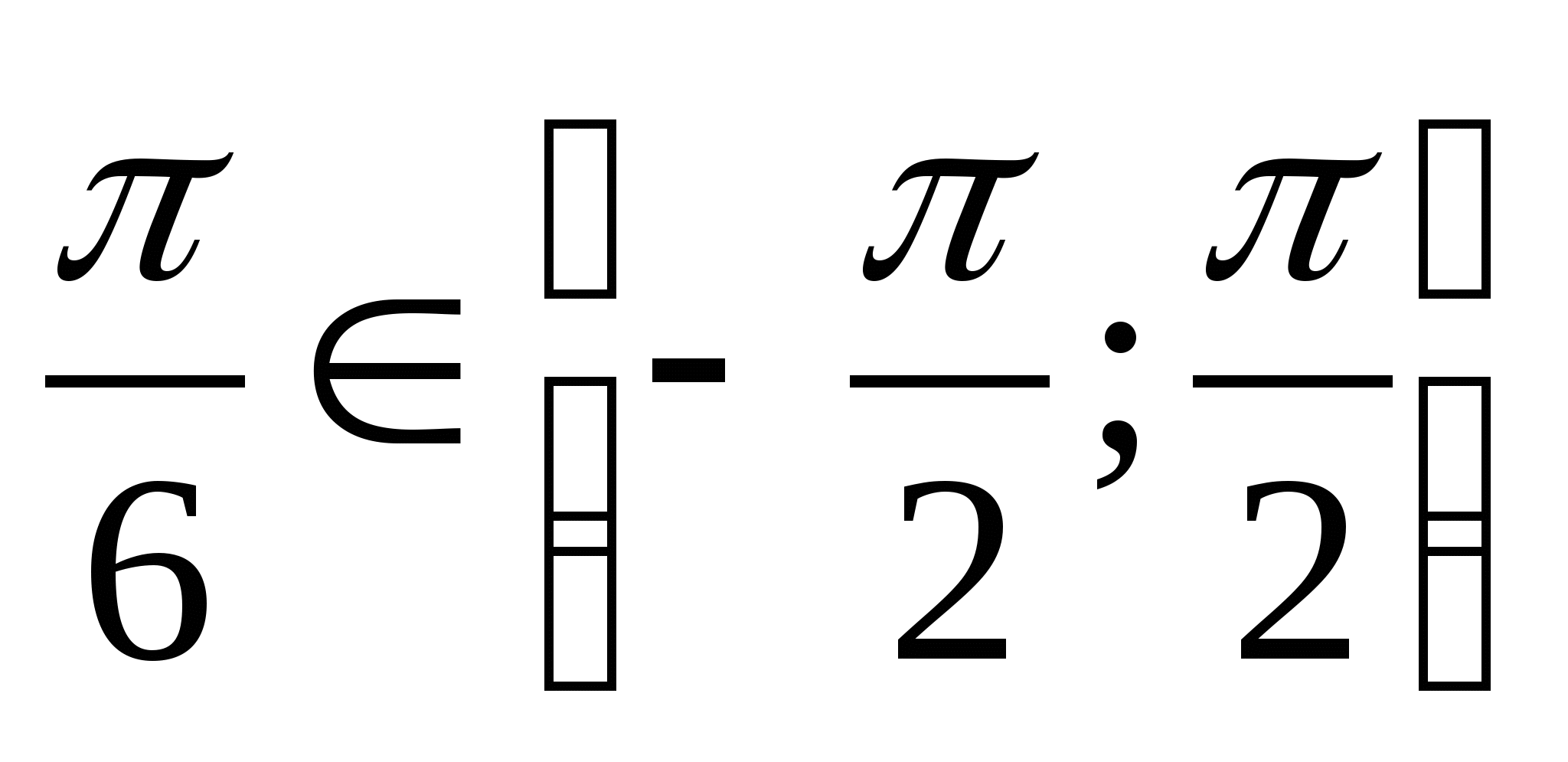Решение. а) Так как и , то .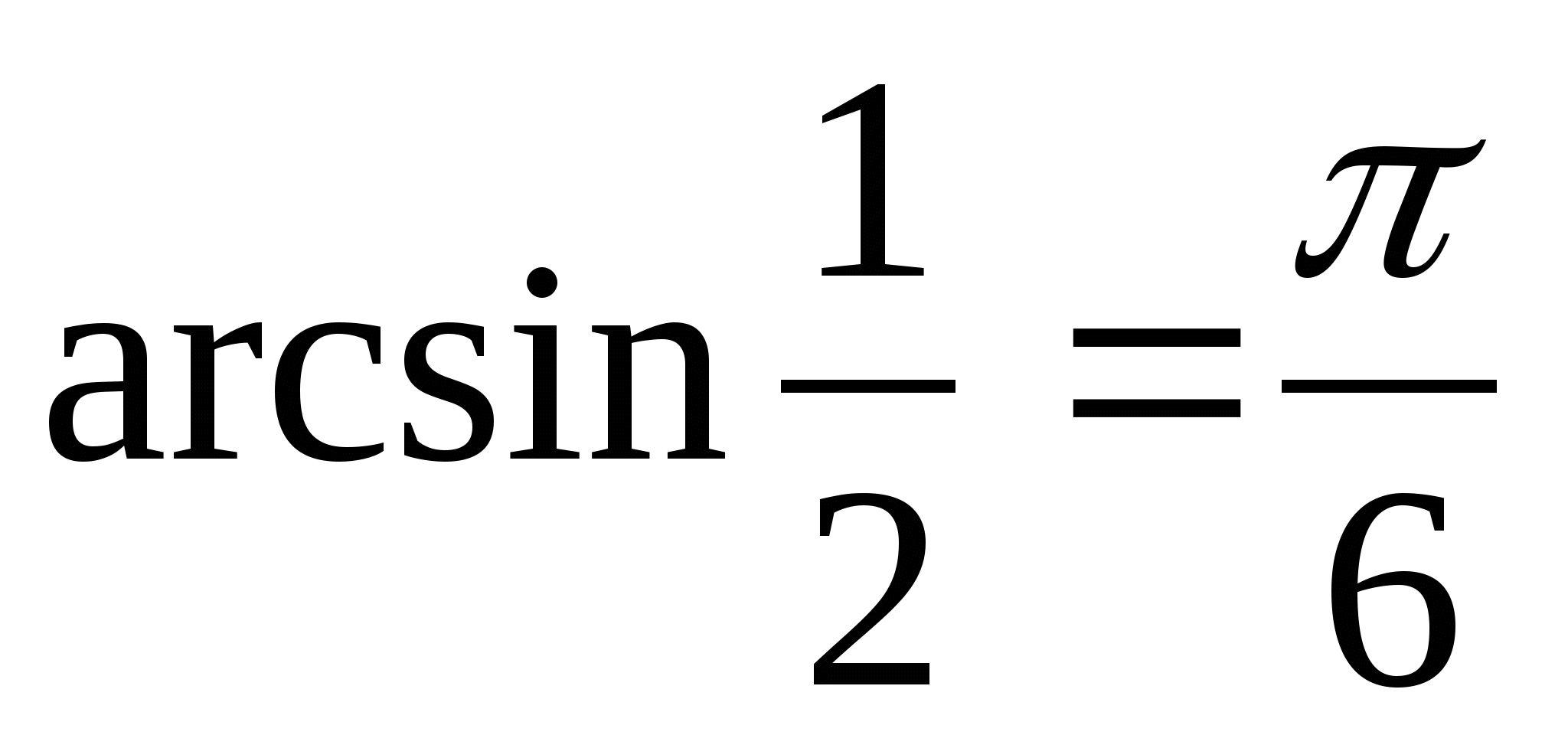

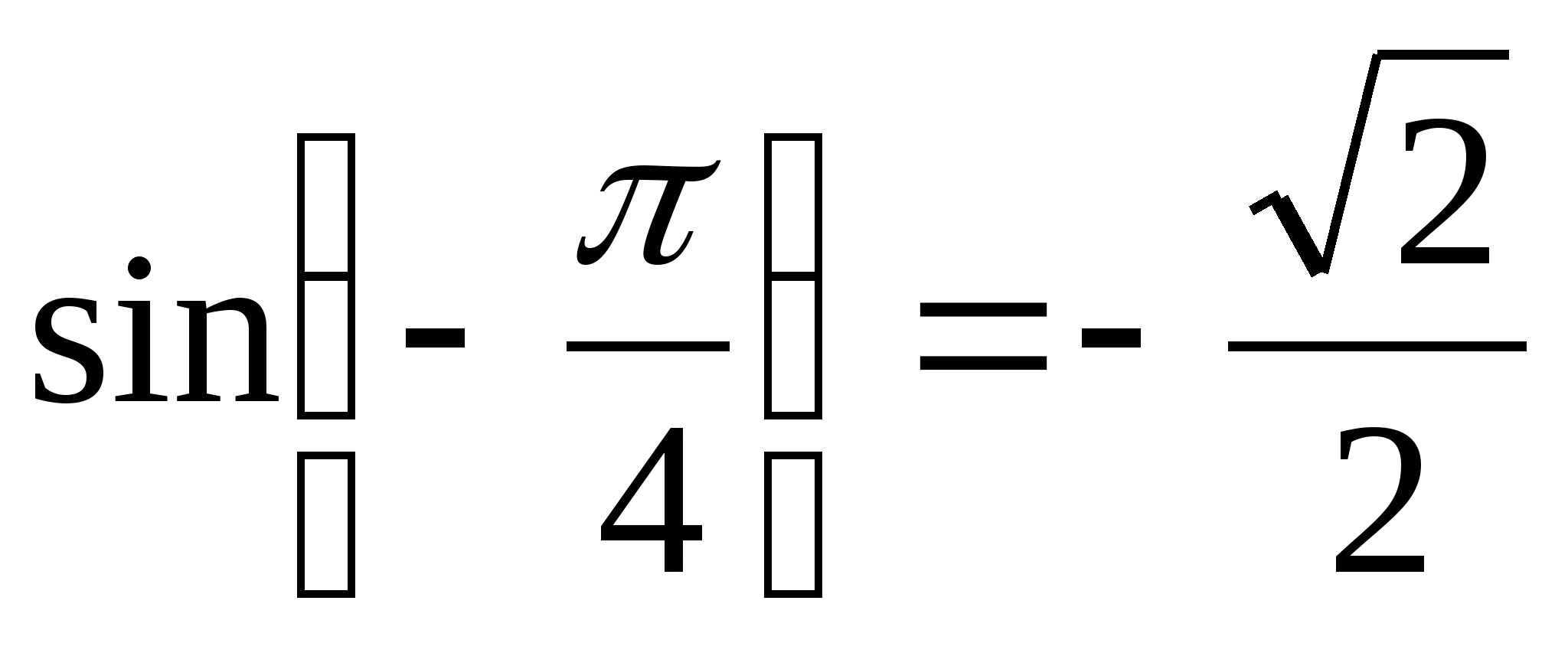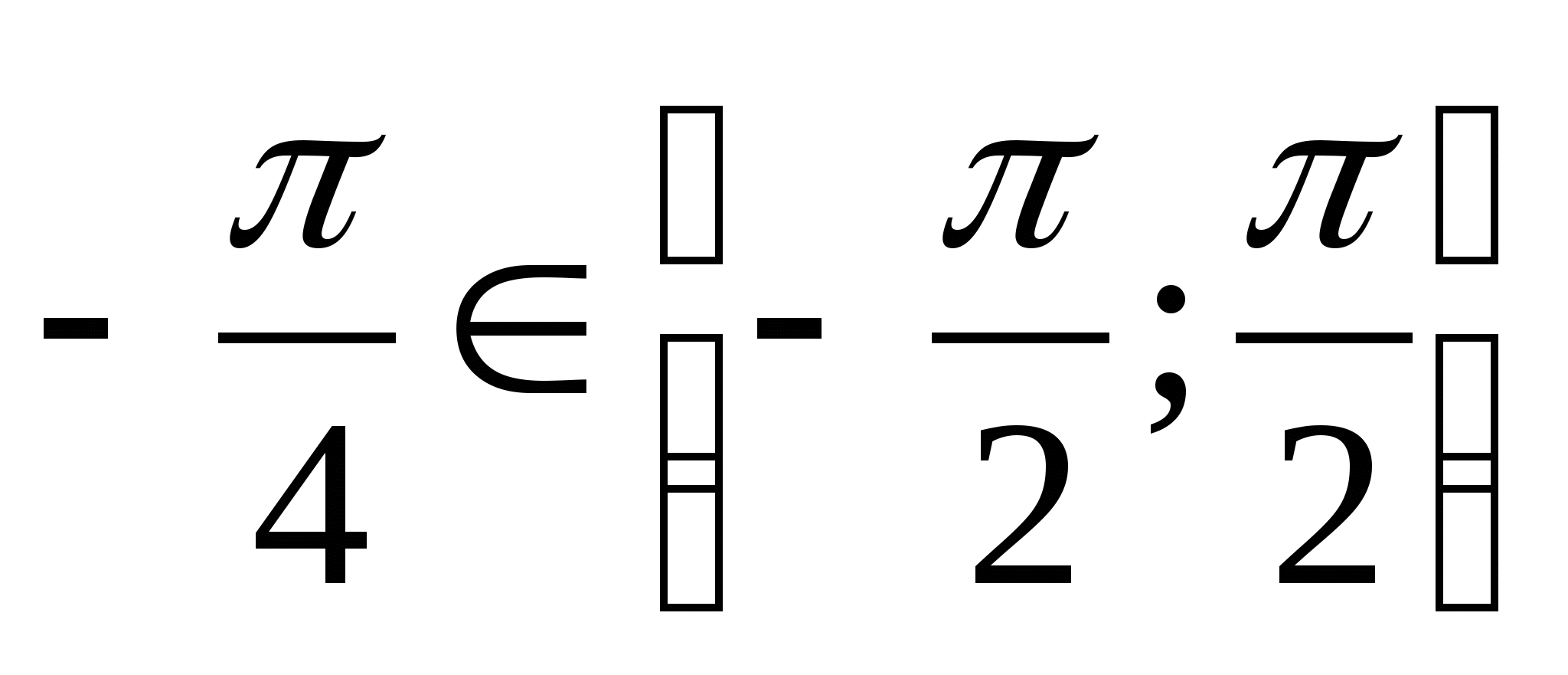б) Так как и , то .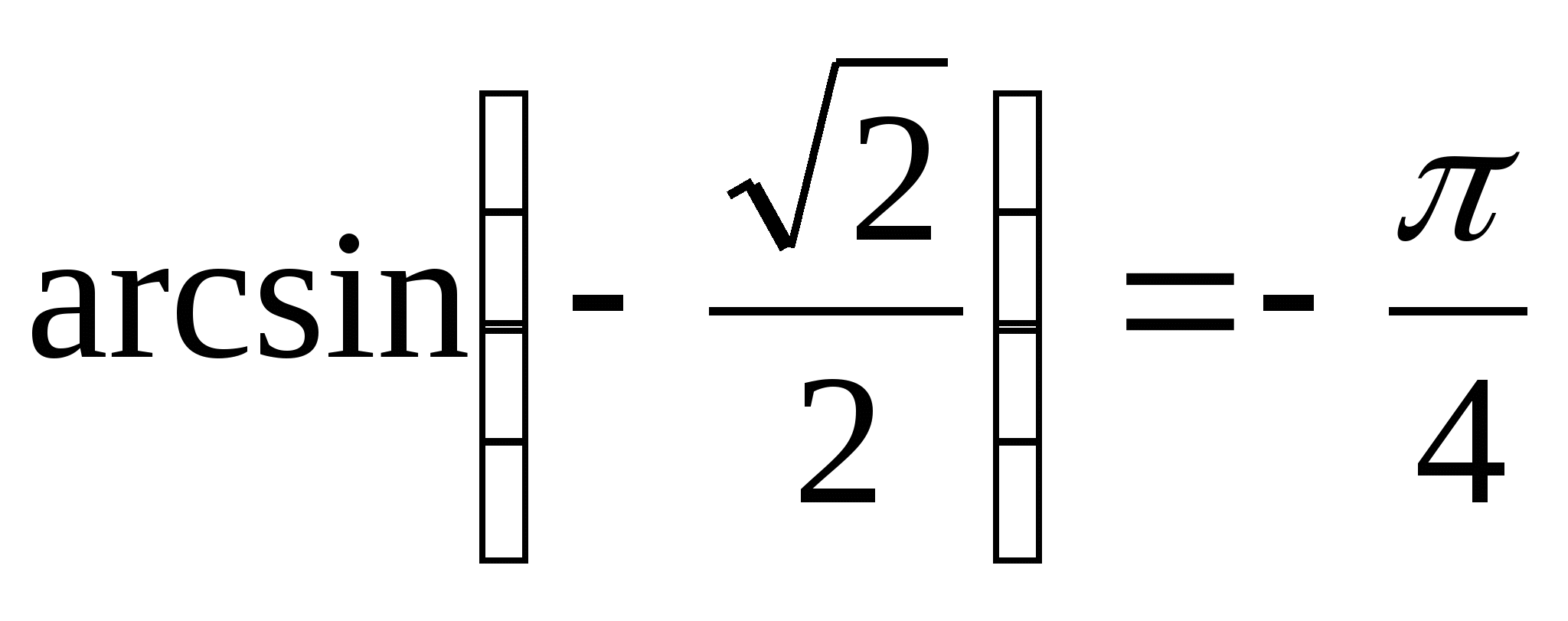

 

 

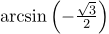
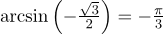
2. Арккосинус. Определение.

 

Арккосинусом числа α называется такое число из отрезка 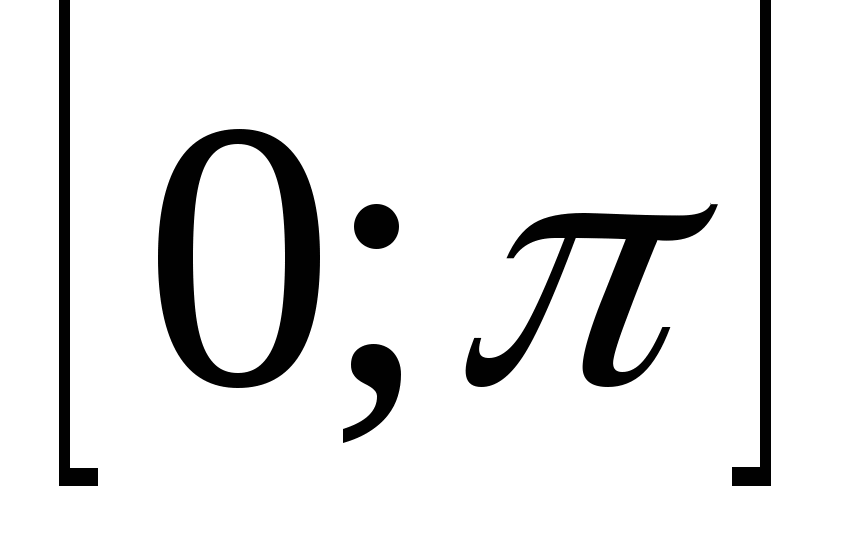, косинус которого равен α.

 

Пример 2. Вычислите: а) ; б) .

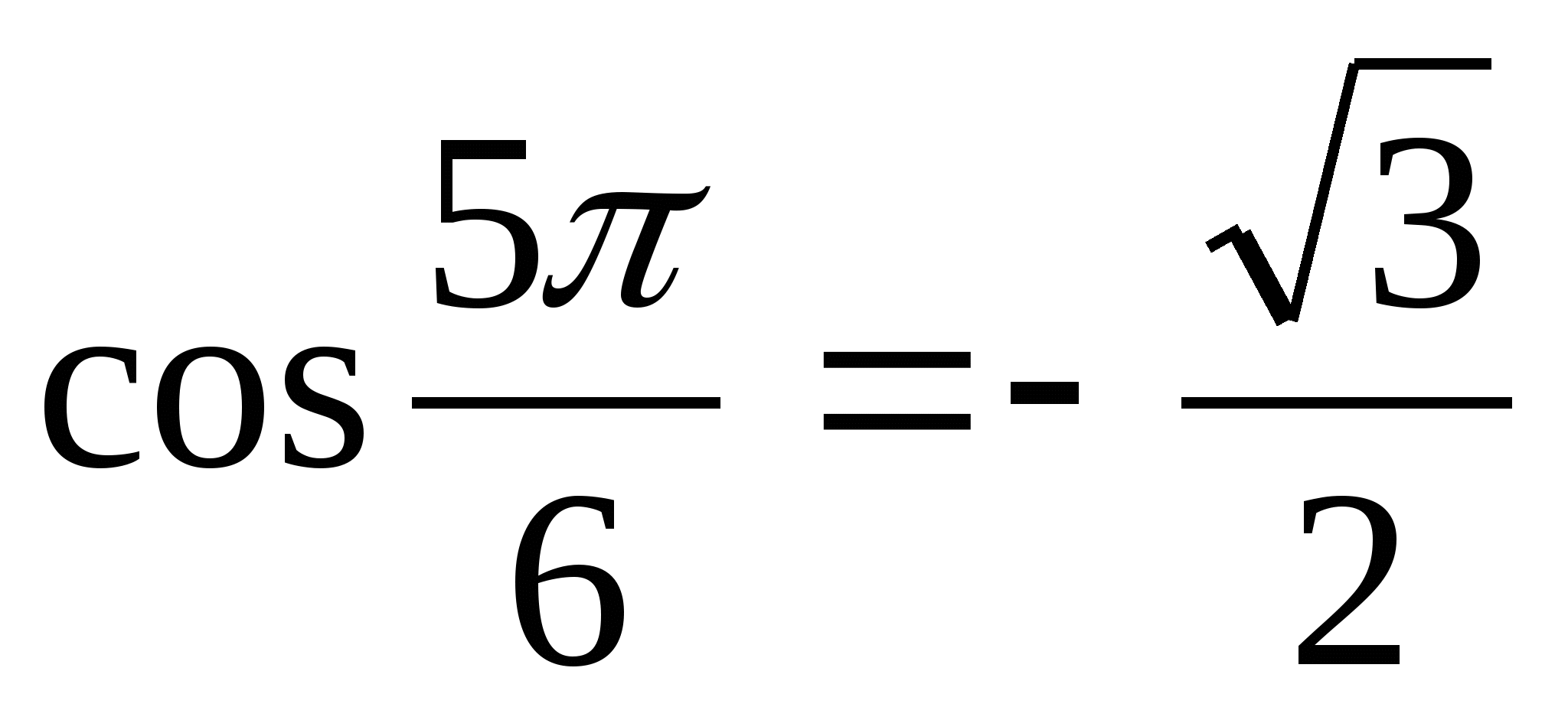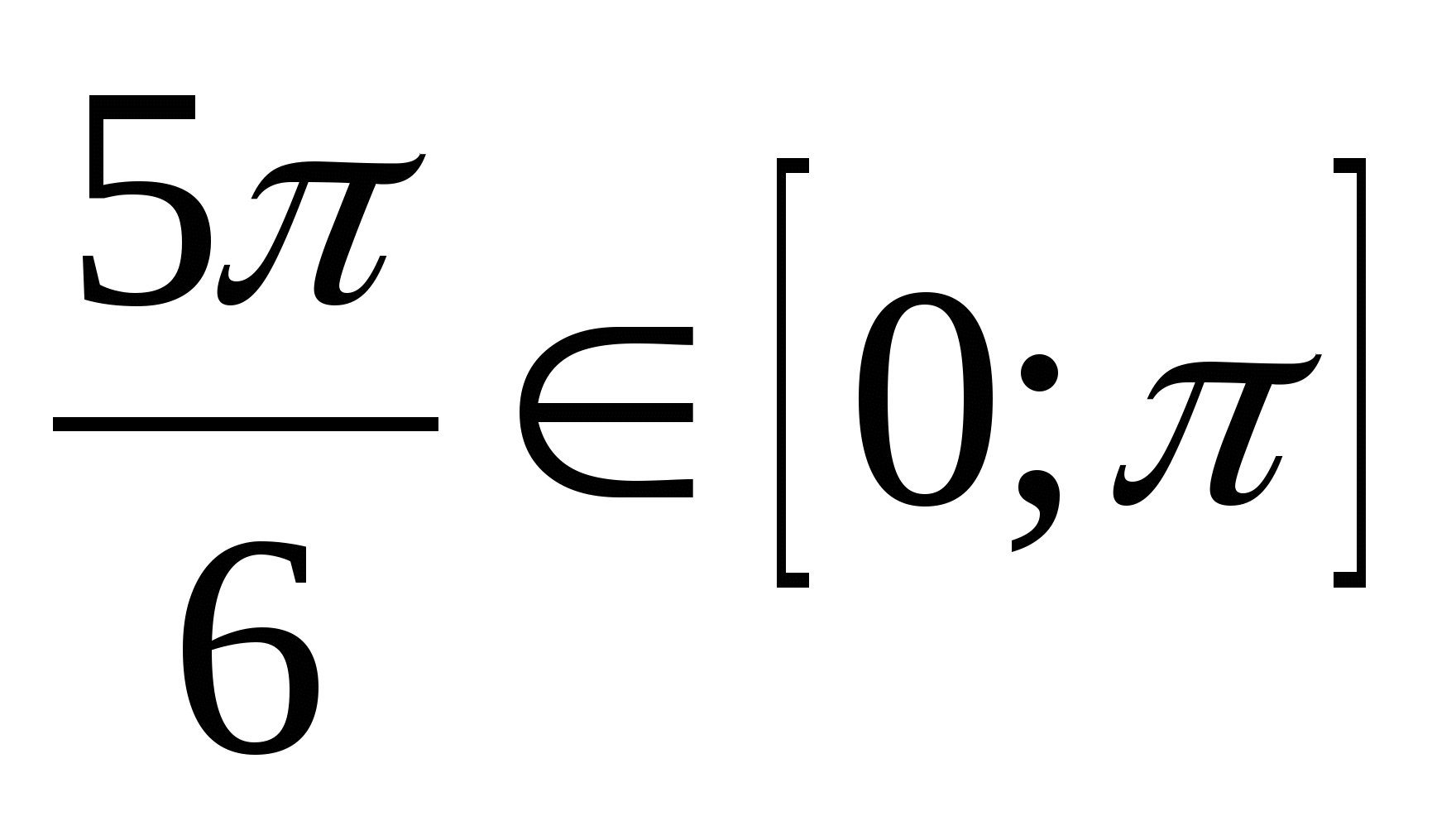Решение. а) Так как и , то .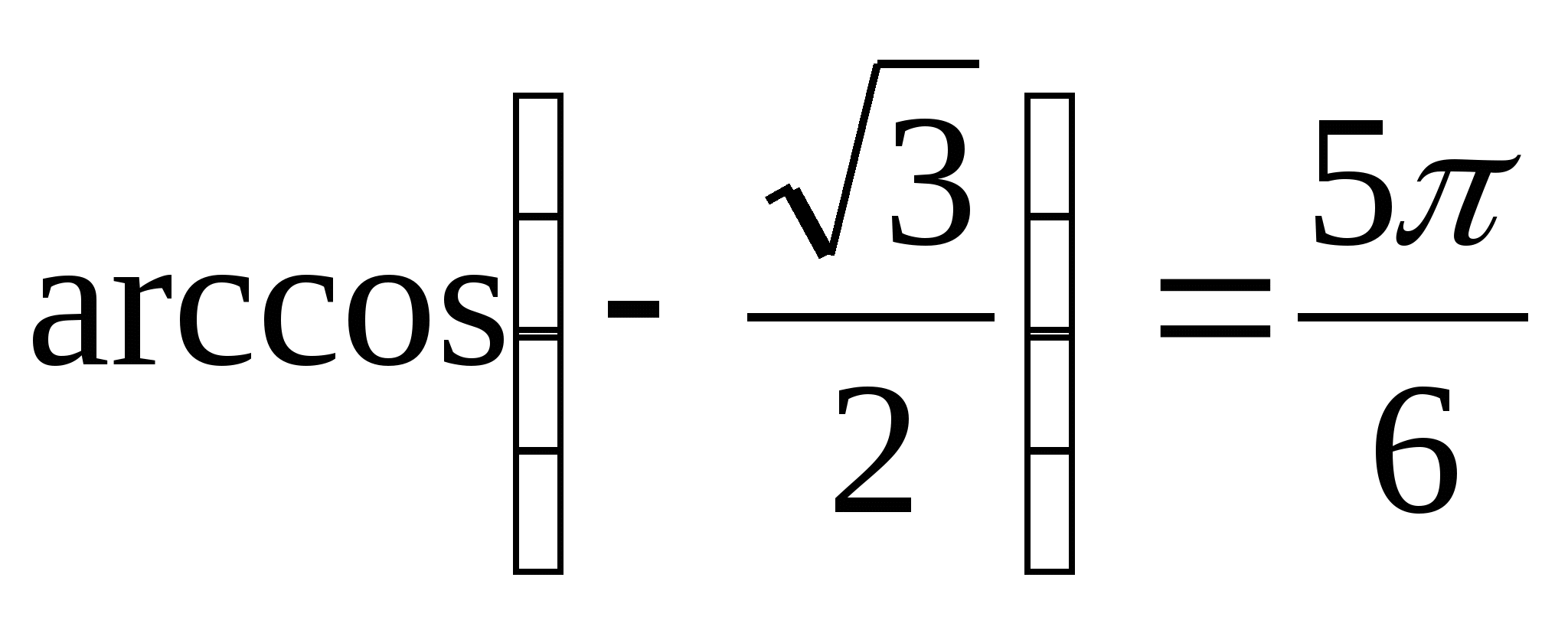

б) Так как 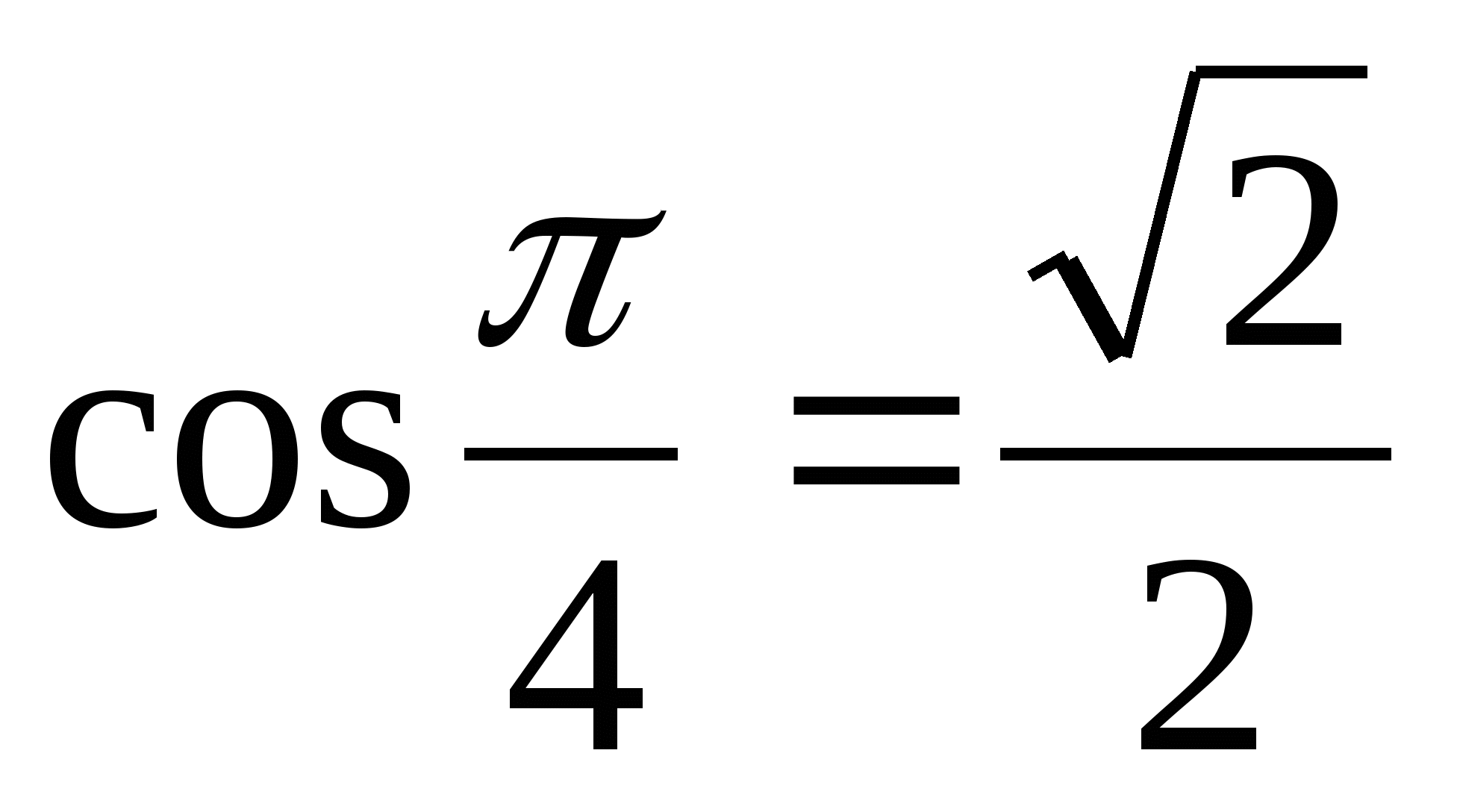и , то .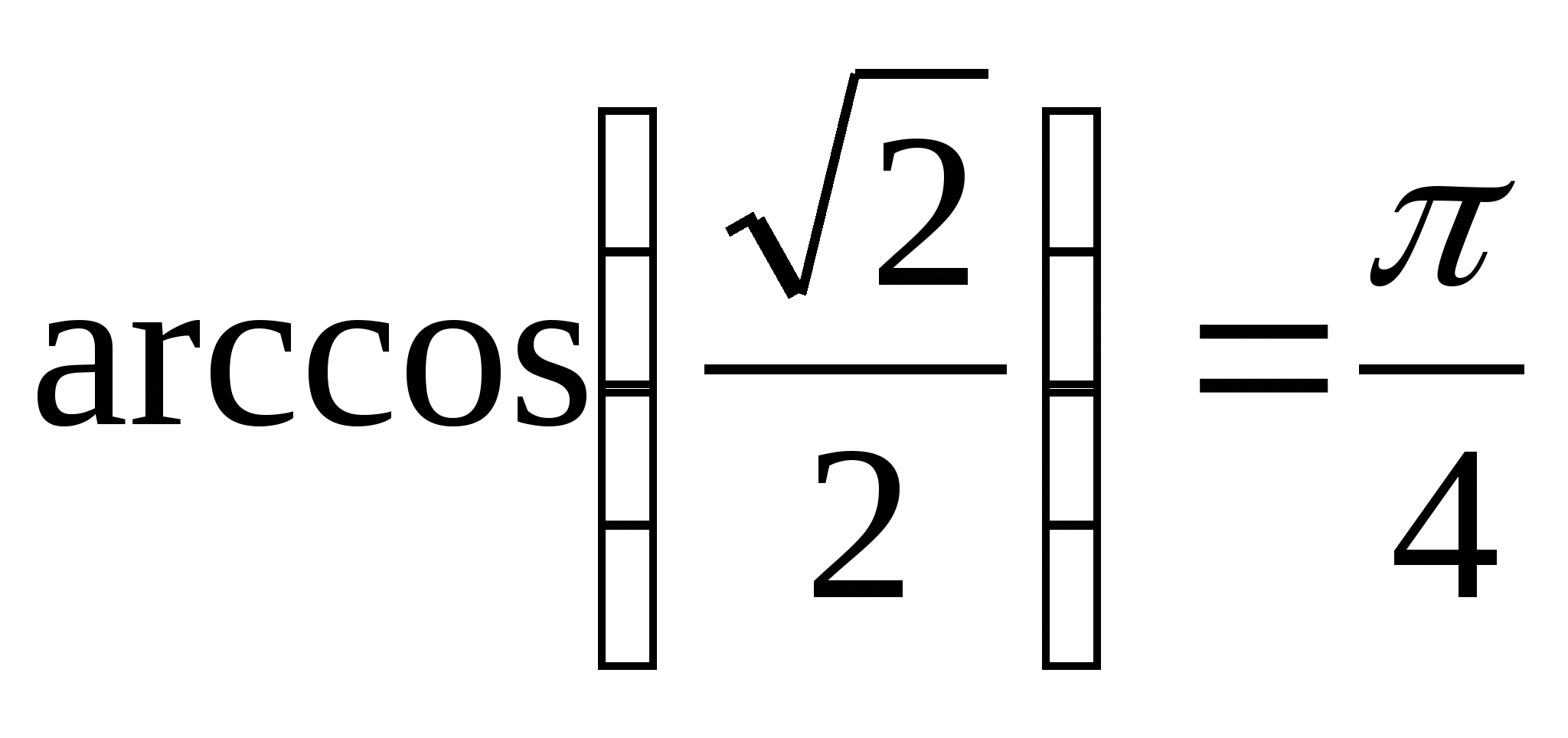

 

3. Арктангенс. Определение.

 

 

Арктангенсом числа α называется такое число из интервала 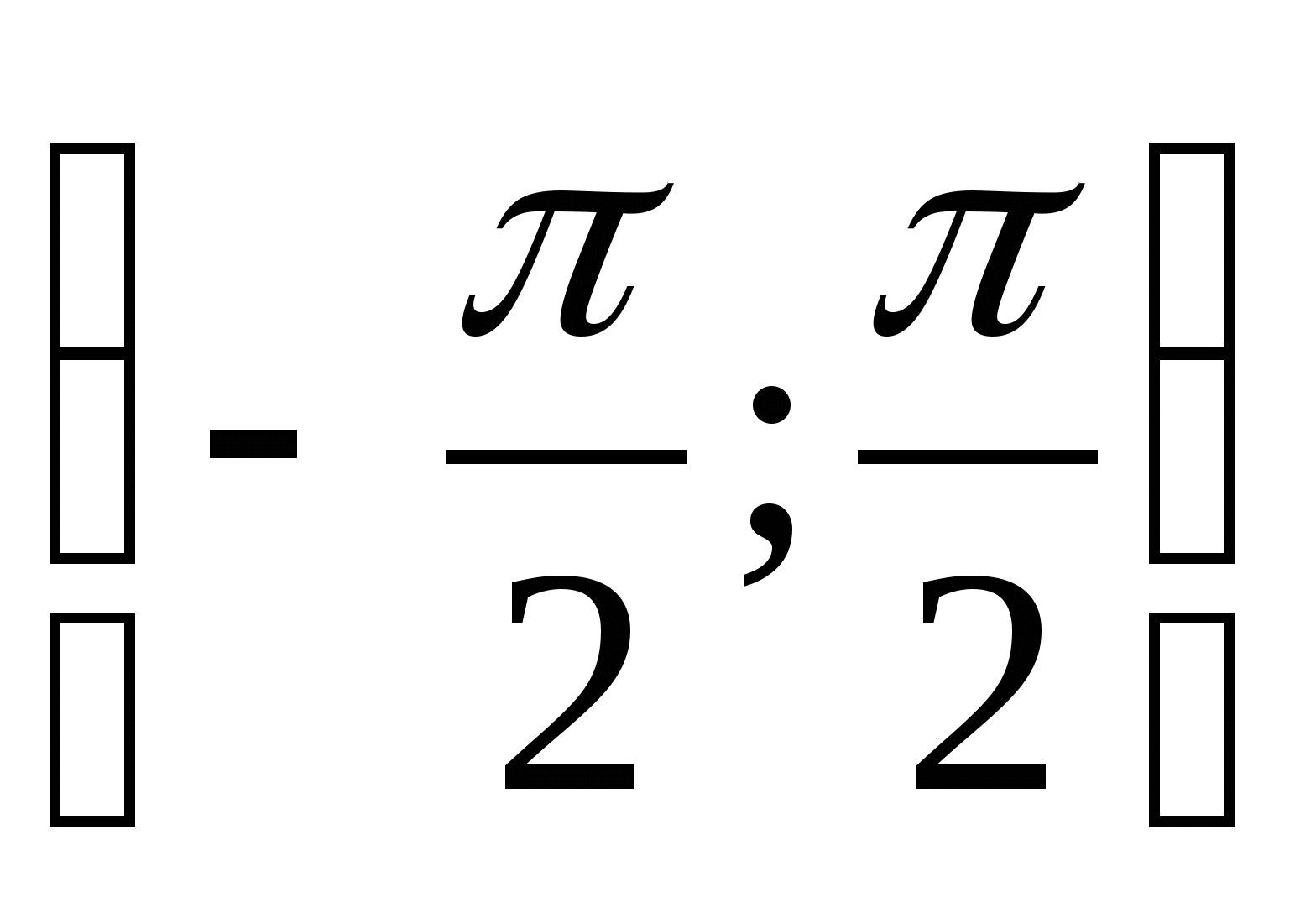, тангенс которого равен α.

 

 

Пример 3. Вычислите: а) ; б) .

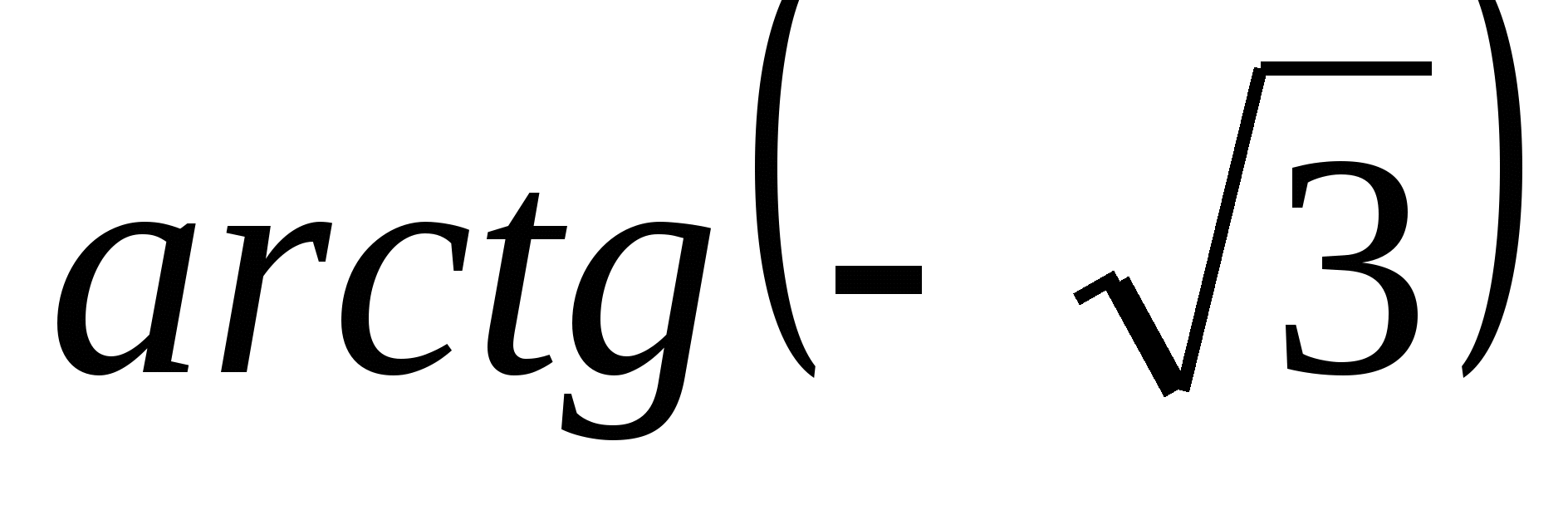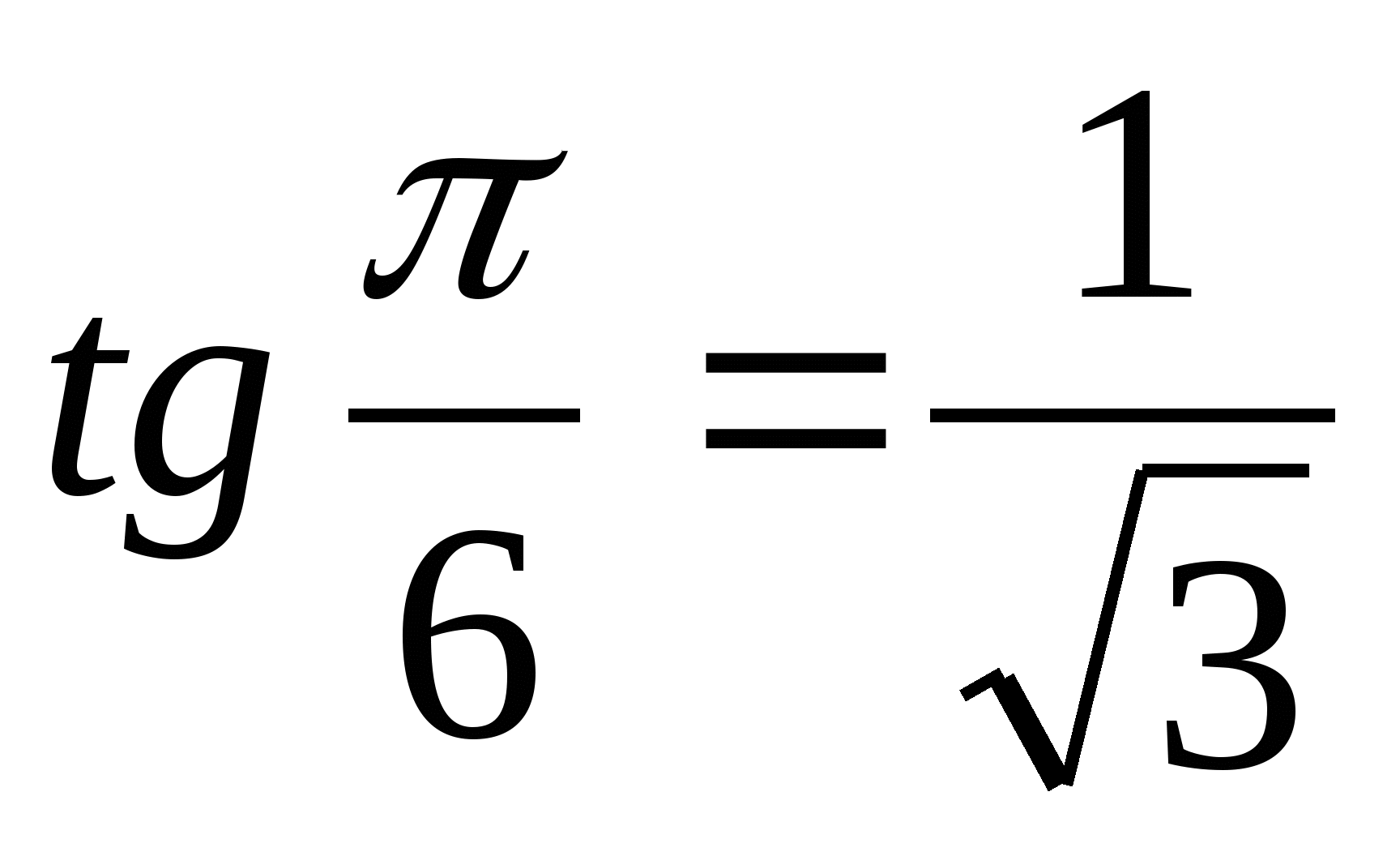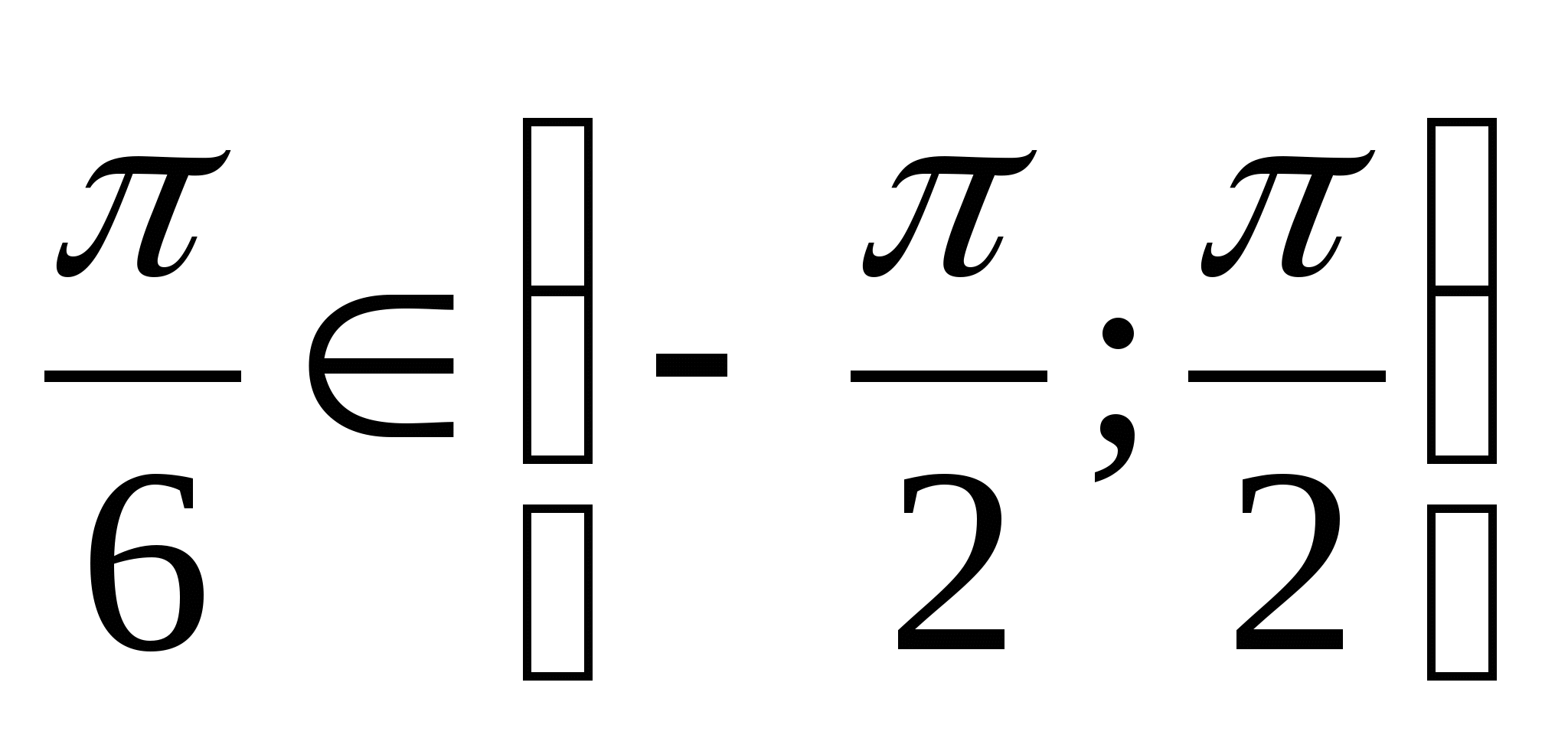Решение. а) Так как и , то .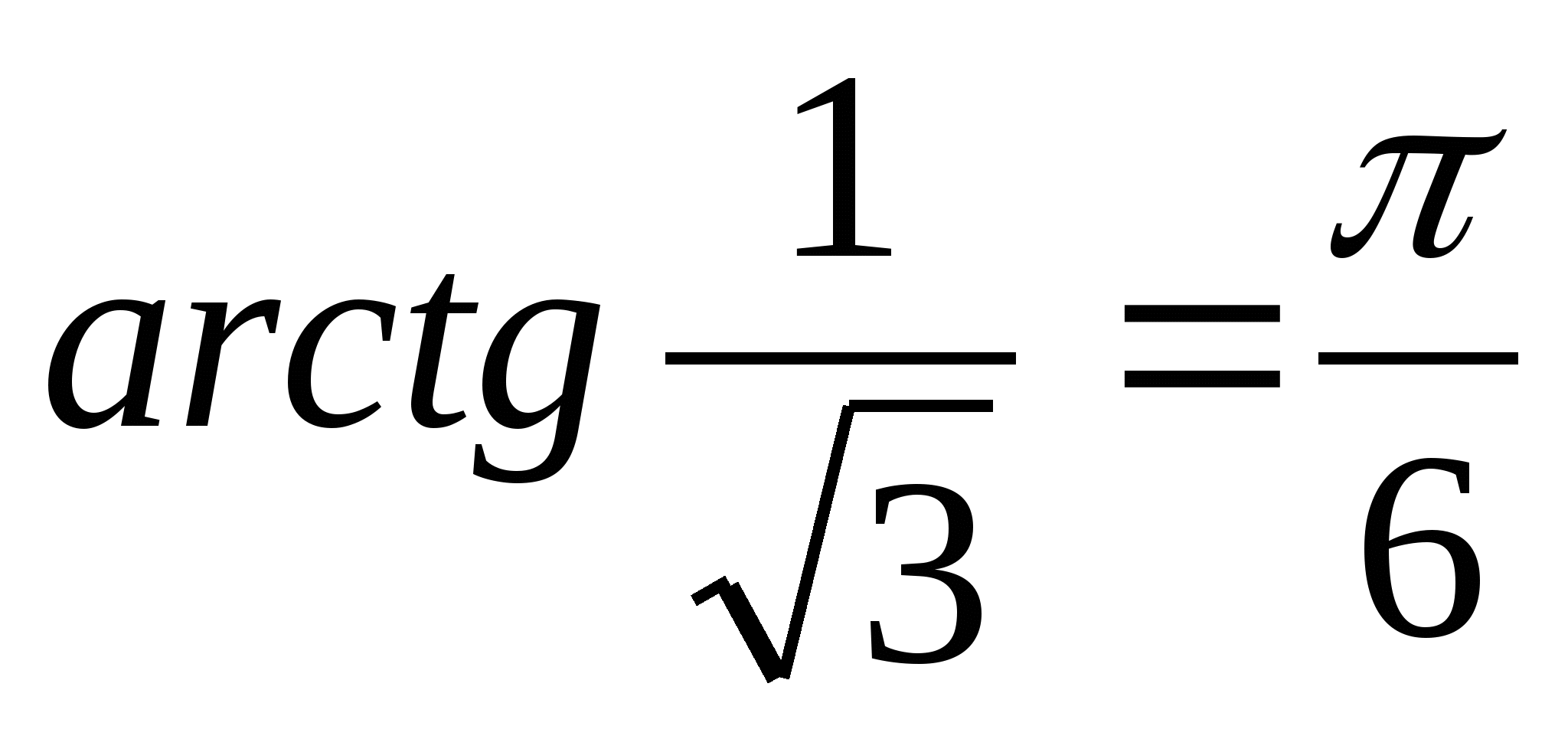

б) Так как и , то .

4. Арккотангенс. Определение.

 

Арккотангенсом числа α называется такое число из интервала 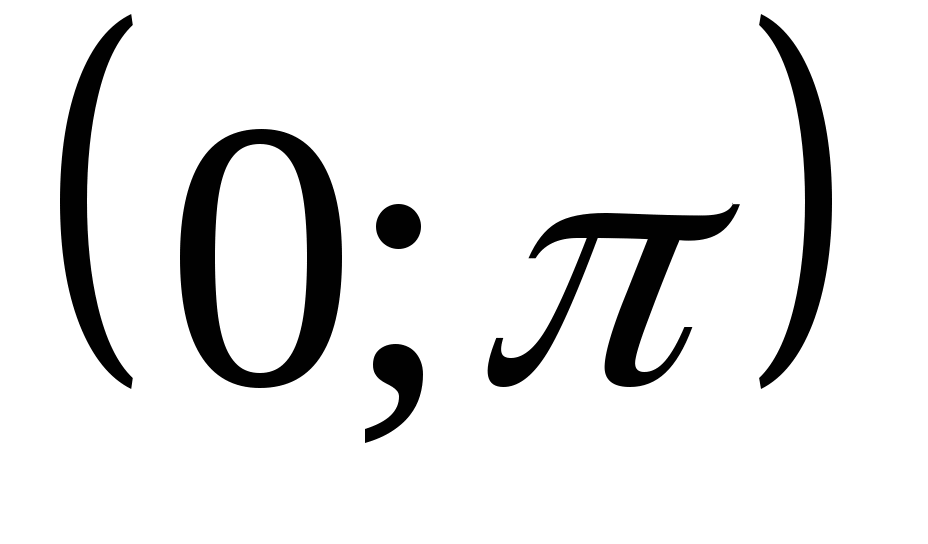, котангенс которого равен α.

 

Пример 4.Вычислите: а) 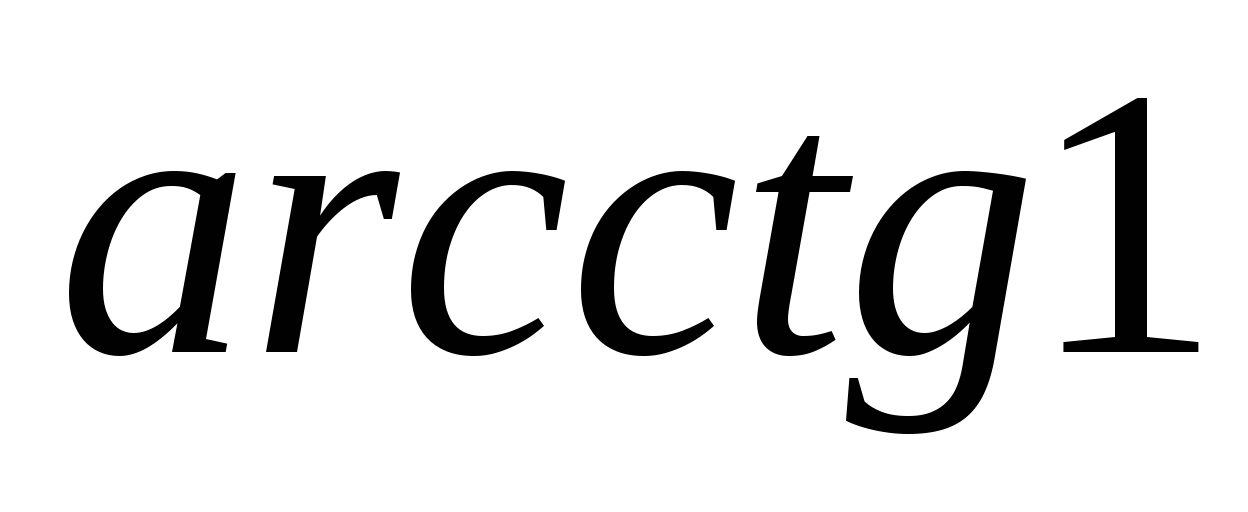; б) .

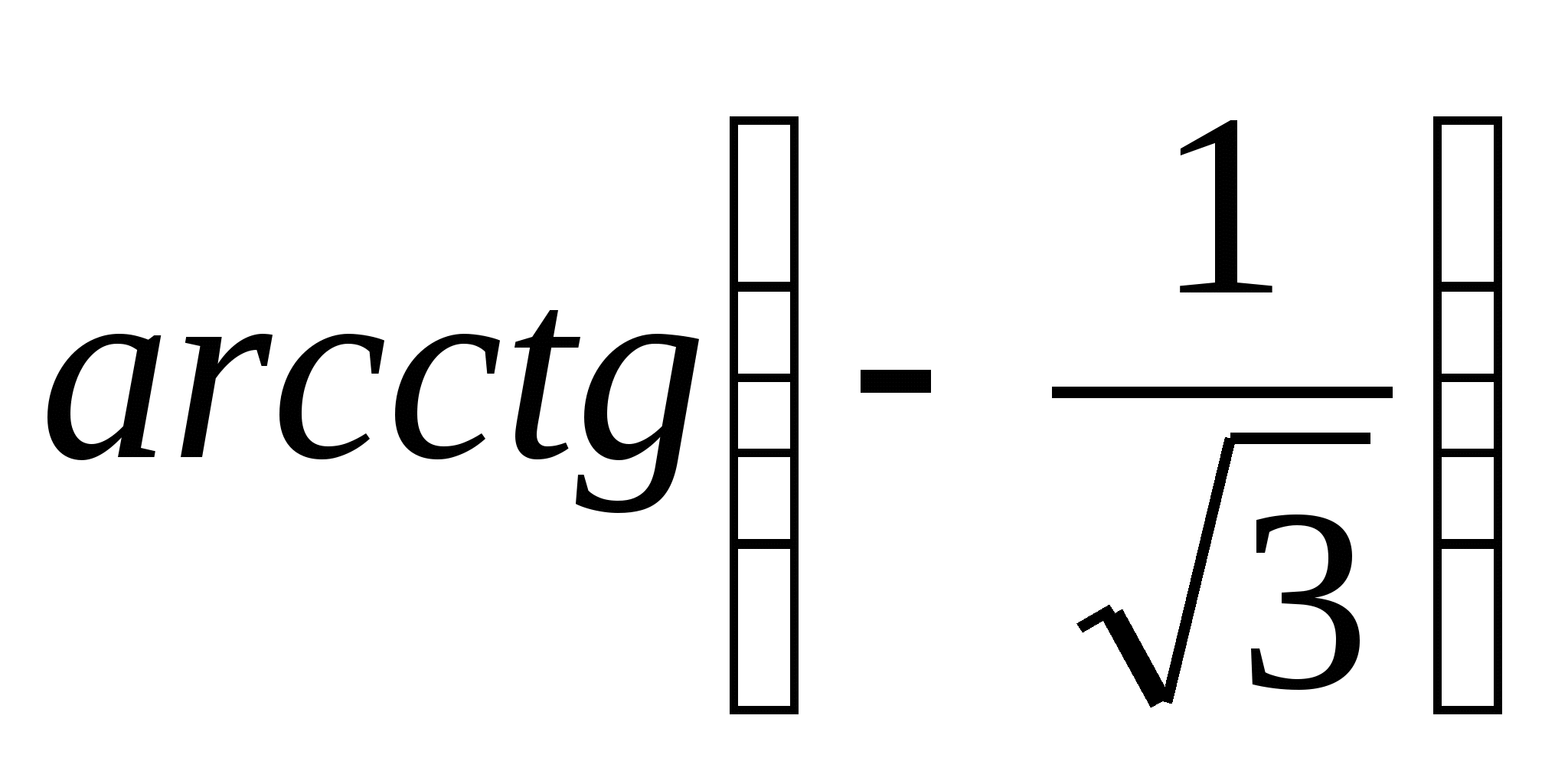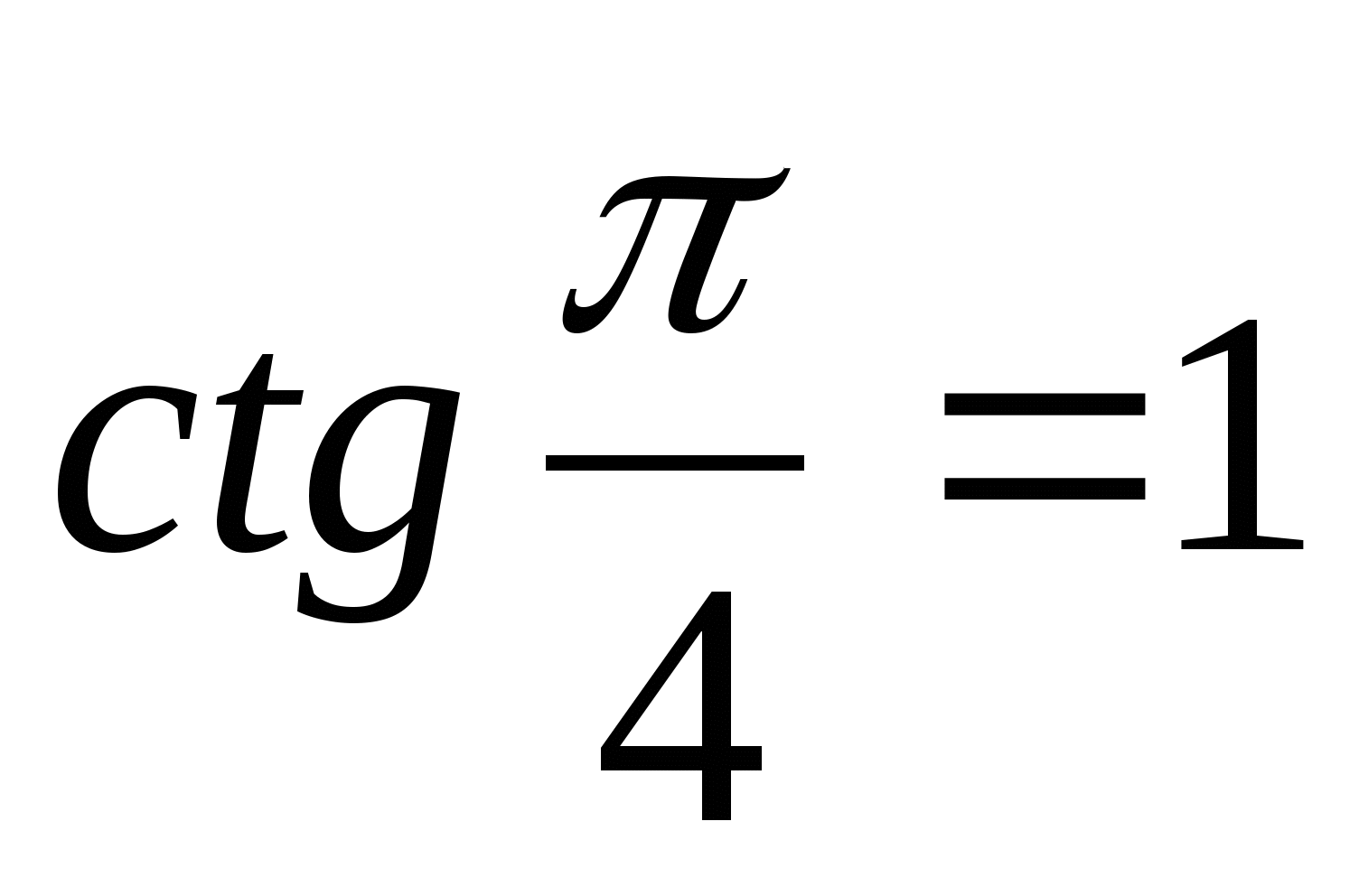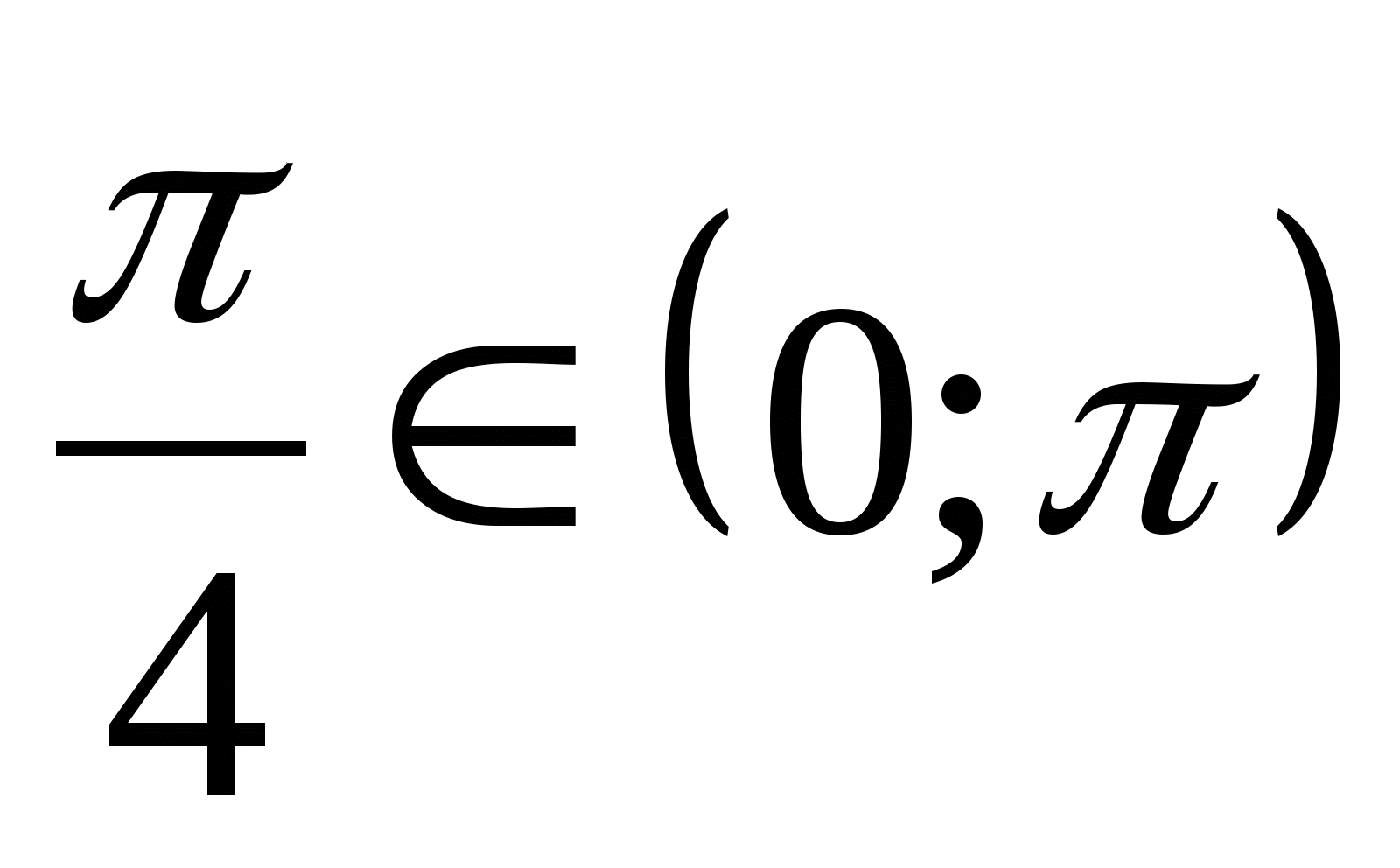Решение. а) Так как и , то .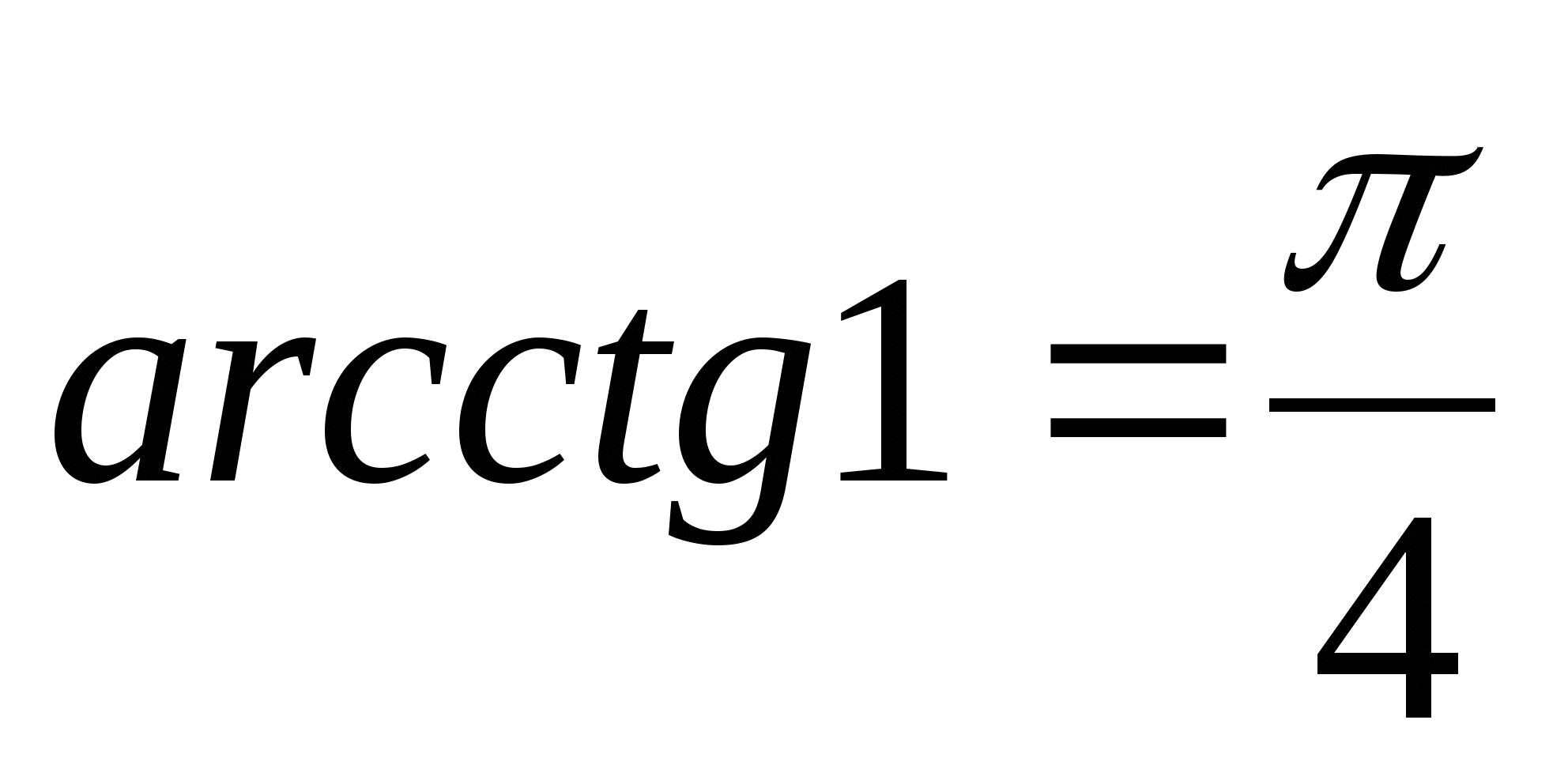

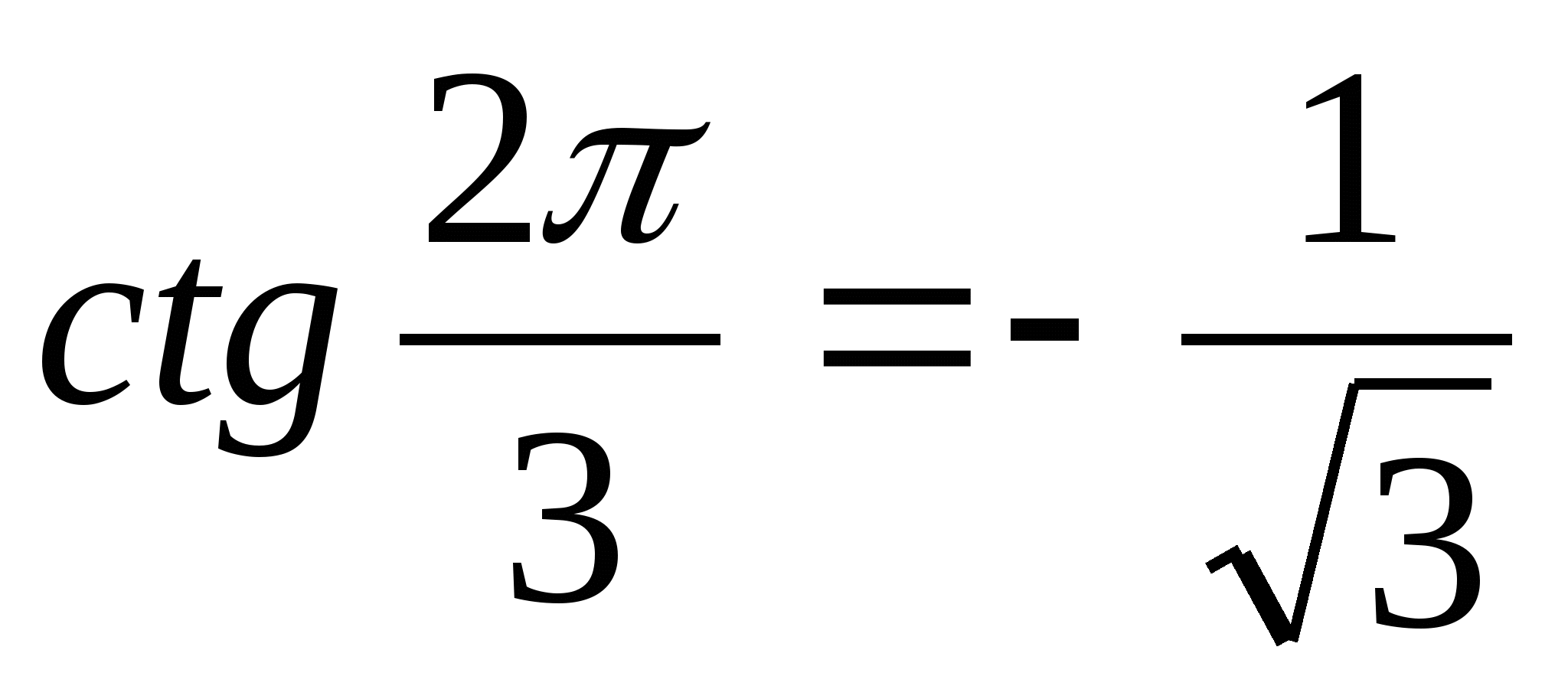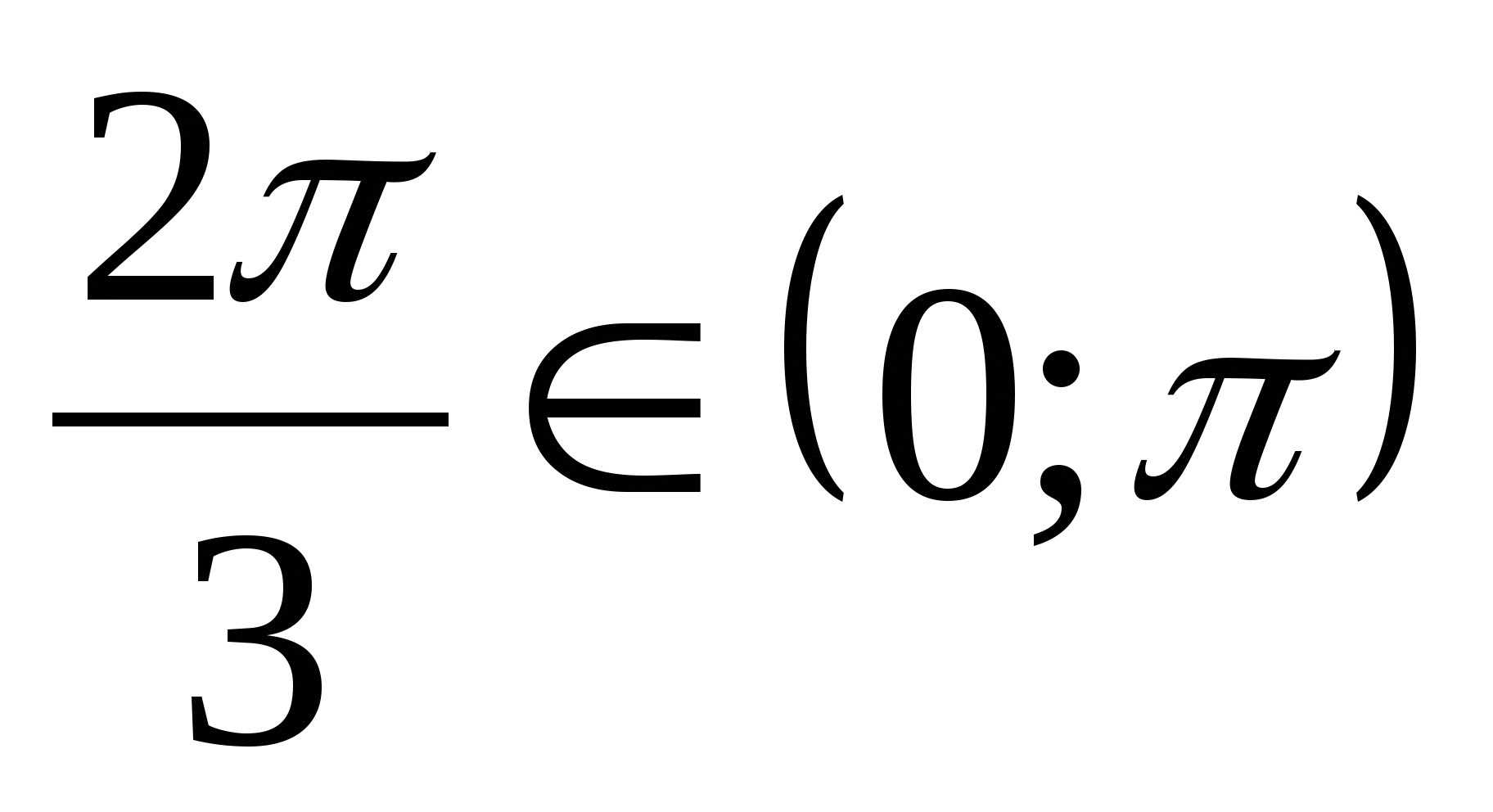б) Так как и , то .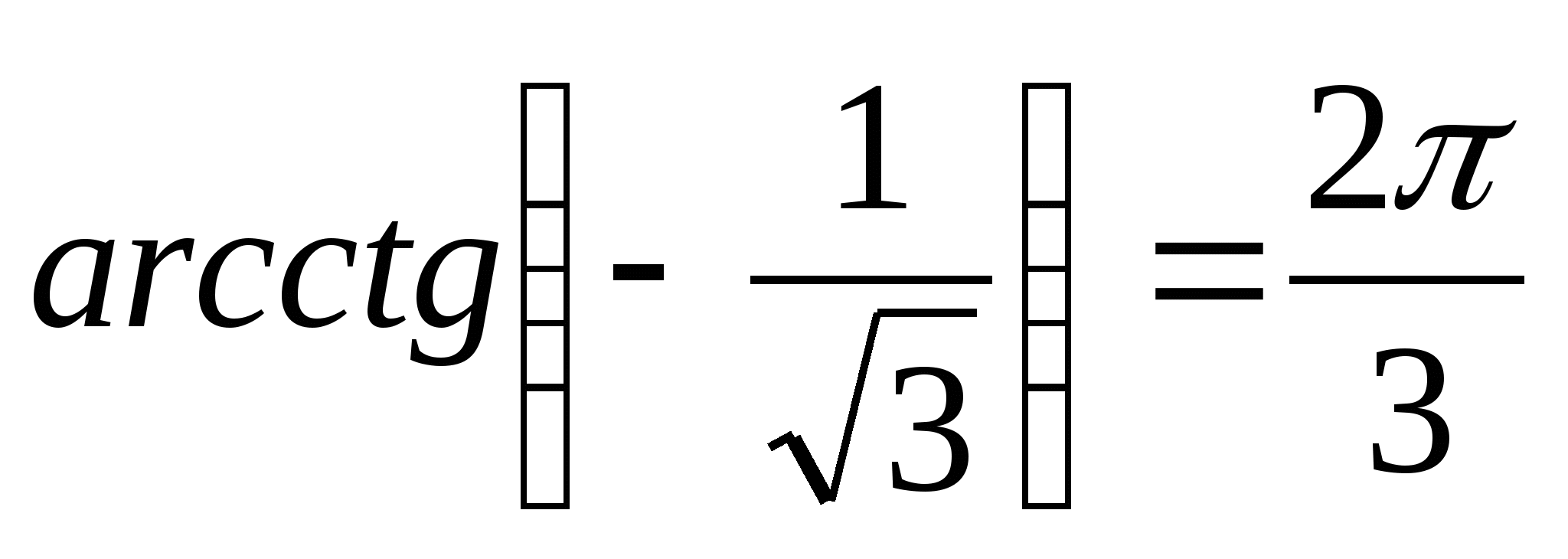

Пример №128

Задания для самостоятельного выполнения

Алгебра и начала анализа под редакцией Колмогорова

п.8 стр. 64-68  №№ 121(а,-г), 122(а-г) 126(а-г)

 
  

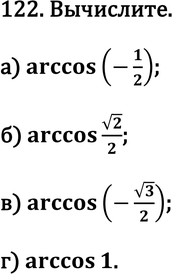
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.