Хелпикс

Главная

Контакты

Случайная статья



V3: {{102}} 04.07.15. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (нахождение частного решения)

⇐ ПредыдущаяСтр 21 из 21


V3: {{102}} 04.07.15. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (нахождение частного решения)

I:{{1026}} Э,С; t=0; k=3; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 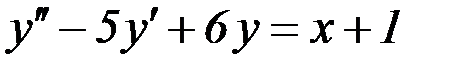по виду его правой части соответствует функция ###

 

-:

-:

+:

-:

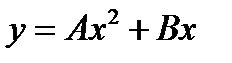
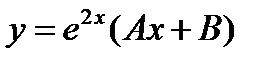
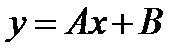
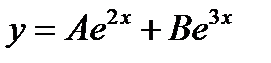
I:{{1027}} Э,С; t=0; k=4; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 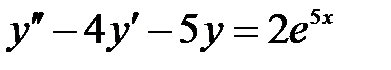по виду его правой части соответствует функция ###

 

-:

+:

-:

-:

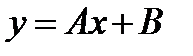
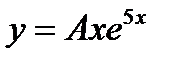
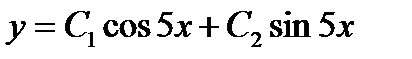
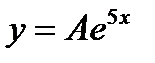
I:{{1028}} Э,С; t=0; k=3; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 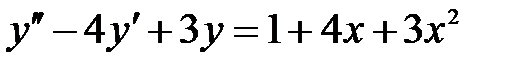по виду его правой части соответствует функция ###

 

+:

-:

-:

-:

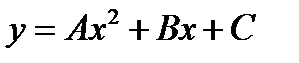
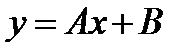
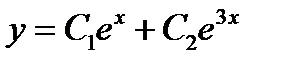
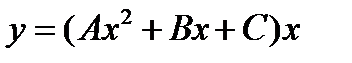
I:{{1029}} Э,С; t=0; k=4; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 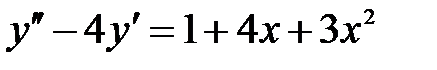по виду его правой части соответствует функция ###

 

-:

-:

-:

+:

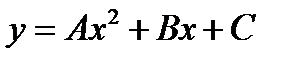
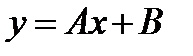
I:{{1030}} Э,С; t=0; k=4; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 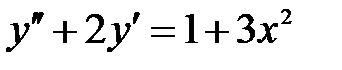по виду его правой части соответствует функция ###

 

-:

-:

-:

+:

I:{{1031}} Э,С; t=0; k=4; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 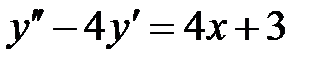по виду его правой части соответствует функция ###

-:

+:

-:

-:

I:{{1032}} Э,С; t=0; k=3; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 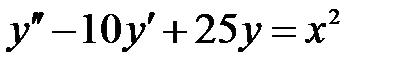 по виду его правой части соответствует функция ###

 

+:

-:

-:

-:

I:{{1033}} Э,С; t=0; k=4; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 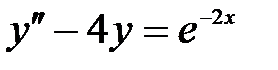 по виду его правой части соответствует функция ###

 

-:

-:

+:

-:

I:{{1034}} Э,С; t=0; k=3; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 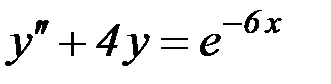по виду его правой части соответствует функция ###

 

-:

-:

+:

-:

I:{{1035}} Э,С; t=0; k=3; ek=0; m=0; c=0;

S: Частному решению линейного неоднородного дифференциального уравнения 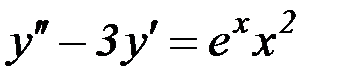по виду его правой части соответствует функция ###

 

-:

+:

-:

-:

 


⇐ Предыдущая12131415161718192021
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.