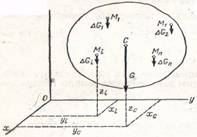
Центр тяжести твердого тела. Xc=(∑Xi∆Gi)/G; Yc=(∑Yi∆Gi)/G;. Zc=(∑Zi*∆Gi)/G.

Центр тяжести твердого тела

Для тел размеры которых малы по сравнению с Земным радиусом, силы тяжести действующие на частицы тела можно считать параллельными друг к другу и сохраняющими для каждой частицы постоянную величину при любых поворотах тела.

Поле тяжести в котором выполняются эти 2 условия называются однородным полем тяжести.

Центром тяжести ТТназывается неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующ. Сил при любом положении тела в пр-ве.

Обозначим силы притяжения отдельных элементарных частиц тела к Земле ∆G1,∆G2, ... , ∆Gn, вес тела G, координаты его центра тяжести

Хс, Ус, Zс, а координаты любой частицы твердого тела — Xi,Yi,Zi. Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил.

Для центра тяжести формулы:

Xc=(∑Xi*∆Gi)/G; Yc=(∑Yi*∆Gi)/G;

Zc=(∑Zi*∆Gi)/G.

В этих формулах алгебраическими величинами являются только координаты точек, а значения ∆Gi всегда положительны, так как все силы направлены в одну сторону.

По формулам этим формулам можно также вычислять координаты центра тяжести тела, разбивая его не на элементарные частицы, а на отдельные части веса Gi, координаты Xi, Yi,Zi центров тяжести которых известны.

Центр тяжести однородного тела. Вес однородного тела определяется формулой G = ᵞ * V, где V — объем тела, ᵞ — вес единицы объема.

Вес каждой частицы определяется по формуле ∆Gi = ᵞ *∆Vi , где ∆Vi-объем элементарной частицы Мiтела.

Xi,Yi,Zi -координаты центра тяжести этой частицы.

Xc=(∑Xi*∆Gi)/G=(∑Xi* ᵞ *∆Vi)/ ᵞ * V = (ᵞ *∑Xi*∆Vi)/ ᵞ * V,

Xc=(∑ Xi*∆Vi )/V,Yc= (∑Yi*∆Vi )/V ,Zc=(∑Zi*∆Vi )/V .

Центр тяжести однородного тела, заполняющего некоторый объем, называется центром тяжести этого объема.

Для однородной пластины. Xc=(∑Xi*Si)/∑Si, Yc=(∑Yi*Si)/∑Si

Для однородной пространственной линии. Xc= =(∑Xi*Li)/∑Li, Yc=(∑Yi*Li)/∑Li, Zc=(∑Zi*Li)/∑Li.

Центр тяжести твердого тела. Xc=(∑Xi*∆Gi)/G; Yc=(∑Yi*∆Gi)/G;. Zc=(∑Zi*∆Gi)/G.

Центр тяжести твердого тела. Xc=(∑Xi∆Gi)/G; Yc=(∑Yi∆Gi)/G;. Zc=(∑Zi*∆Gi)/G.