
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание: изучить материал урока, выписать формулы производных элементарных функций, выполнить задания на закрепление материала и домашнюю работу.
Задание: изучить материал урока, выписать формулы производных элементарных функций, выполнить задания на закрепление материала и домашнюю работу.
Урок
Тема:Производные основных элементарных функций.
Цели урока:
Образовательные: познакомить учащихся с формулами нахождения производных элементарных функций; учить находить производные элементарных функций.
Ход урока.
1. Изучение нового материала
Формула дифференцирования степенной функции
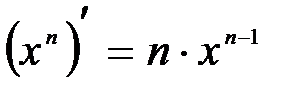
Приняв 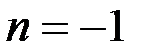 и
и 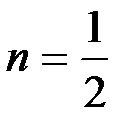 , получаются следующие формулы:
, получаются следующие формулы:
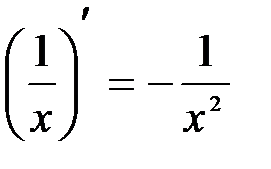 и
и 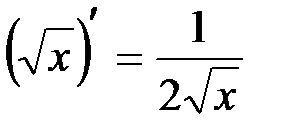
Формула дифференцирования показательной функции
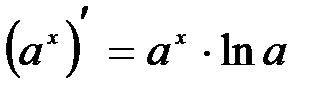
В случае 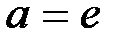 , применяя определение натурального логарифма, для числа е получаем формулу:
, применяя определение натурального логарифма, для числа е получаем формулу:
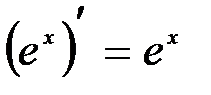
Формулы дифференцирования тригонометрических функций
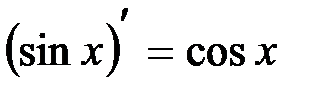

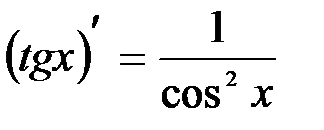
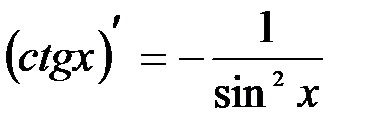
Формула дифференцирования логарифмической функции
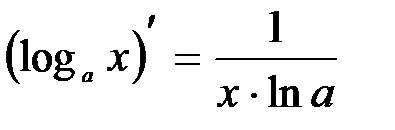 . В частности,
. В частности, 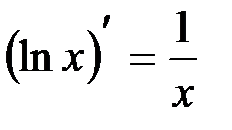 .
.
Применяя формулы производных основных элементарных функций и правила дифференцирования, мы можем решить бесконечное множество задач на нахождение производной функции.
Рассмотрим примеры:
Пример 1:
Найти производную функции 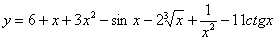
Производную обозначаем штрихом!

Обратите внимание, что для дифференцирования все корни, степени нужно представить в виде 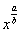 , а если они находятся в знаменателе, то переместить их вверх. Применяем правило производной суммы и правило дифференцирования – постоянные множители (числа) выносим за знак производной:
, а если они находятся в знаменателе, то переместить их вверх. Применяем правило производной суммы и правило дифференцирования – постоянные множители (числа) выносим за знак производной:

Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Но это выражение можно упростить:

Пример 2:
Найти производную функции 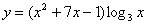
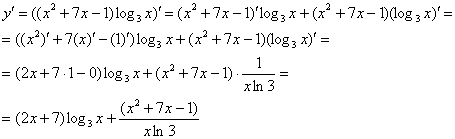
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|