Комплексные числа , представить в тригонометрической, показательной формах и вычислить : 4а) ; 4б) .

0-ВАРИАНТ

Контрольной работы №1 по дисциплине «Математика»

для студентов 1 курса (1 семестр)

Модуль 1: «Элементы теории множеств». Модуль 2: «Комплексные числа»

1) В классе 40 человек. Из них по русскому языку имеют тройки 19 человек, по математике – 17 человек и по физике – 22 человека; по русскому или математике - 25, по русскому или физике – 32; по физике или математике – 32. Пять человек имеют тройки по русскому языку, математике и физике. Сколько человек учатся без троек? Сколько человек имеют тройки только по математике? Сколько человек имеют тройки по русскому языку и по физике?

2)Найти множество 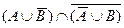, если Е={1,2,3,4,5} ,A={1,5},B={1,2,4}

3.Даны комплексные числа , ,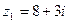

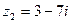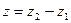
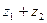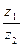Найти: 3а) ; 3б) 3в) ; 3г) - .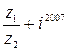

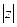4.Комплексные числа , представить в тригонометрической, показательной формах и вычислить : 4а) ; 4б) .

5а)Решить уравнение: . 5б)Найти .

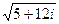6.Построить на комплексной плоскости множество точек, удовлетворяющих условию: (или , или , или , или ).

_________________________________________________________

ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ К РАБОТЕ №1

1. Множества. Примеры. Операции над множествами. Мощность множества.

2. Декартовы прямоугольные координаты на плоскости.

3.Полярные координаты. Зависимость между полярными и прямоугольными координатами (с выводом).

4.Натуральные числа. Целые числа. Теорема (о существовании иррационального числа 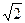). Иррациональные числа. Действительные числа.

5 Комплексные числа. Действительная и мнимая части комплексного числа. Модуль. Сопряженное число. Геометрическое изображение комплексных чисел.

6.Сумма, разность, умножение, деление комплексных чисел (с доказательством).

7.Тригонометрическая форма комплексного числа. Умножение и деление комплексных чисел в тригонометрической форме (с доказательством).

8.Формула Эйлера.Показательная форма комплексного числа. Примеры.

ЛИТЕРАТУРА

1. Шипачев В.С., Высшая математика, М. «Высшая школа»,2005.

2. Куликов Л.Я., Алгебра и теория чисел, М. «Высшая школа»,1979.

3. Курош А.Г., Курс высшей алгебры, М. Изд. «Наука», 1971.

4. КремерН. Высшая математика для экономистов