
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
В1Формулы дифференцирования В2 Таблица основных интегралов
В1Формулы дифференцирования В2 Таблица основных интегралов
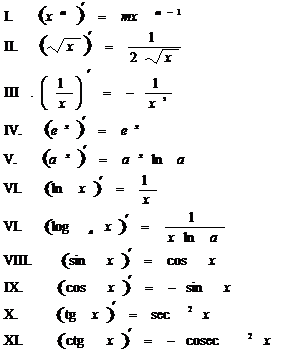
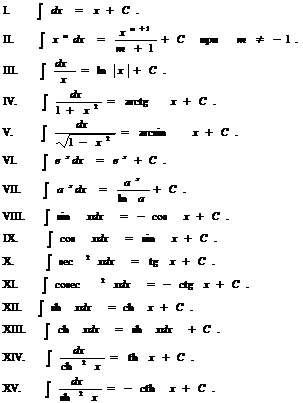 |
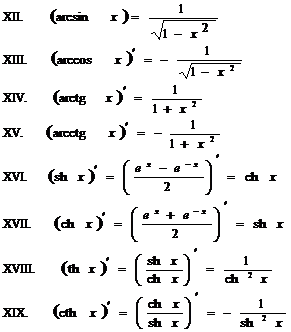
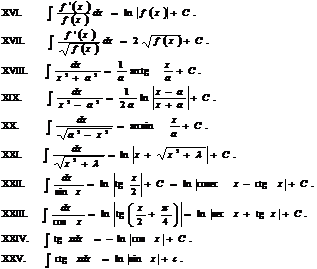 |
Правила интегрирования
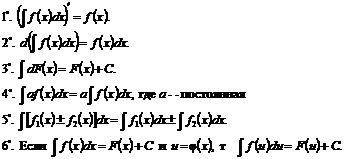 |
Основные правила дифференцирования
Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие
производные.
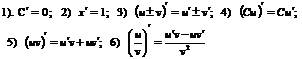 | |||
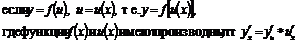 | |||
7)

В 4 Интегрирование по частям Основные свойства
определённого интеграла
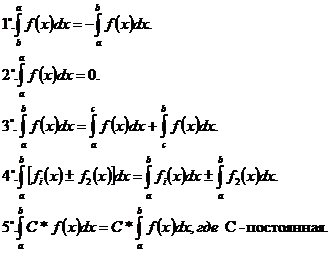 |
Интегрирование простейших дробей
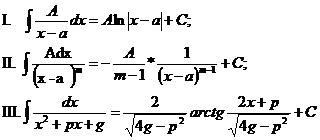 |
Замена переменной в
неопределенном интеграле
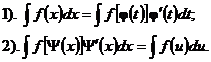

Площадь плоской фигуры
 Площадь криволинейной трапеции, ограниченной кривой
Площадь криволинейной трапеции, ограниченной кривой  , прямыми
, прямыми 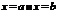 и отрезком[a, b] оси Ox, вычисляется по формуле
и отрезком[a, b] оси Ox, вычисляется по формуле
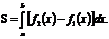 Площадь фигуры, ограниченной кривыми
Площадь фигуры, ограниченной кривыми 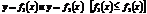 и прямыми
и прямыми 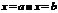 , находится по формуле
, находится по формуле
Если кривая задана параметрическими уравнениями 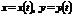 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми 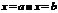 и отрезком[a, b] оси Ox, выражается формулой
и отрезком[a, b] оси Ox, выражается формулой
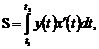
где 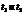 определяются из уравнений
определяются из уравнений 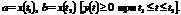
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением 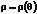 и двумя полярными радиусами
и двумя полярными радиусами 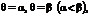 находится по формуле
находится по формуле
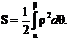
В 6 Длина дуги плоской кривой
Если кривая y=f(x) на отрезке [a, b] – гладкая (т.е. производная 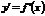 непрерывна), то длина соответствующей дуги этой кривой находится по формуле
непрерывна), то длина соответствующей дуги этой кривой находится по формуле
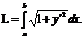 |
При параметрическом задании кривой x=x(t), y=y(t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра 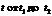 , вычисляется по формуле
, вычисляется по формуле
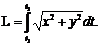 |
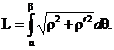 Если гладкая кривая задана в полярных координатах уравнением
Если гладкая кривая задана в полярных координатах уравнением 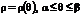 , то длина дуги равна
, то длина дуги равна
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|