Хелпикс

Главная

Контакты

Случайная статья



Лабораторная работа 5.. Численное интегрирование. Вычислить точное значение интеграла для своего варианта.. Вычислить погрешности. Результаты вычислений оформить в виде таблиц.. Сделать выводы о порядке аппроксимации квадратурных формул.. Численные мето



Лабораторная работа 5.

Численное интегрирование

1. Вычислить точное значение интеграла   для своего варианта.

2. Найти 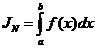 при  N=10 ,  N=20, N=40  по формулам:

· левых прямоугольников,

· правых прямоугольников,

· трапеций,

· средних прямоугольников,

· Симпсона.

3. Вычислить погрешности. Результаты вычислений оформить в виде таблиц.

4. Сделать выводы о порядке аппроксимации квадратурных формул.

 

ВАРИАНТЫ ЗАДАНИЙ.

№ g(x) [a, b] № g(x) [a, b]
2/(1 – x2) [2, 3] 2 –x – 1 [1, 2]
(1–x)/(1 + x2) [ –1, 1] 1/sin2x [p/4, 3p/4]
1/(1 + x2) [2, 3] 1/cos2x [ –p/4, p/4]
(2 – x2)(3 – x) [ –1, 0.5] (1 – x)/x [ –1, 0.5]
Sin(2x) [0, 1] Sin(x) + cos(2x) [ –p/4, p/4]
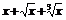
[0, 2] x1/3 + x – 2/3 [1, 2]
1/sin2x [0.5, 1.5] 5/sin2x [p/4, p/2]
3/ 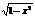[ –p/4, p/4] ex/3 [–0.5,0.5]
ex [ –1, 1] sin(x) – 3 cos (2x) [p/4, p/2]
x2/3 [0, 5] 1/(1 + x)+2/(1 – x2) [–0.5,0.5]
cos(x)–1/2 cos(2x) [ –p, p] cos(x)–1/4 sin(2x) [ –p, p]
sin(x)+1/3sin(3x) [0, 2p] 3/cos2x [0, p/2]
1/(1+x) [1, 3] 5/ [2, 3]
x3– 3x2+2 [0, 1] (x2 – 3x+2)/(x2+1) [0, 1]

Часть 2

Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений

ЗАДАНИЕ.

1. Для своего варианта проверить, что заданная функция  является точным решением, удовлетворяющее начальному условию .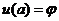

2. Найти решение задачи Коши для обыкновенного дифференциального уравнения первого порядка  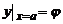на отрезке [a,b], при N=10 , N=20 и N=40

                           А) методом Эйлера

                           Б) модифицированным методом Эйлера

                           В) методом Рунге-Кутта 4 порядка.

3. На основании анализа погрешностей определить порядок аппроксимации каждого метода.

Варианты заданий

№ F(x,y) [a,b]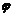
1. 2x-y+x2 [ 0,2] x2
2. 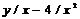[1,3] 2x
3. Sin2x-y2-Cos x [0, ] -sin x
4. 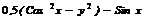[0, ] cos x
5. 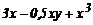[0,2] -2 2(x2-1)
6. [-2,0] x2
7. 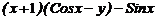[ 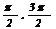]   cos x
8. 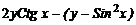[ 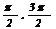]     sin2 x
9. 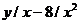[2,5]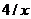
10. 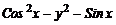[ 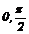]   cos x
11. 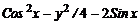[ 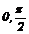]   2cos x
12. 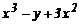[0,2] x3
13. 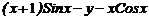[ ] x sin x
14. [0,2] x2/2
15. Sin2(x) ‑y2 ‑ Cos(x) [0, ] -sin(x)
16. 3x ‑ 0.5xy + t3 [0,2] -2 2(x2-1)
17. x [2 + x2 sin(x2) ‑ y sin(y)] [-2,0] x2
18. y/x ‑ 8/x2 [1,3] 4/x
19. 0.5 (sin2(t) ‑y2) + cos(x) [0,p/2] sin(x)
20. cos2(x) ‑y2 ‑ sin(x) [0, p/2] cos(x)
21. 3x3 ‑ y2 + x6 [0,2] x3
22. cos2(x) ‑y2/4 ‑ 2 sin(x) [0, p/2] 2cos(x)
23. (x+0.6)(cos(x) –y) ‑ sin(x) [p/2, 3p/2] cos(x)
24. (x+1) (sin(x) –y)+ cos(x) [p/2, 3p/2] sin (x)
25. 2(x – 2) + x (x ‑ 2)2 –xy [2,4] (x-2)2

1. Метод предиктор-корректор (двухшаговый, второго порядка аппроксимации)

2. Метод Рунге-Кутты 2-1 (двухшаговый, вариант 1, второго порядка аппроксимации)

3. Метод Рунге-Кутты 2-2 (двухшаговый, вариант 2, второго порядка аппроксимации)

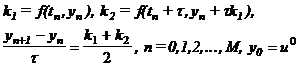
4. Метод Рунге-Кутты 3-1 (трехшаговый, вариант 1, третьего порядка аппроксимации)

5. Метод Рунге-Кутты 3-2 (трехшаговый, вариант 2 третьего порядка аппроксимации)

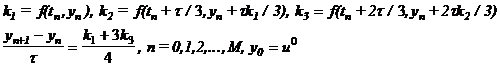
6. Метод Рунге-Кутты 4-1 (четырехшаговый, вариант 1, четвертого порядка аппроксимации)

7. Метод Рунге-Кутты 4-2 (четырехшаговый, вариант 2, четвертого порядка аппроксимации)

 
  

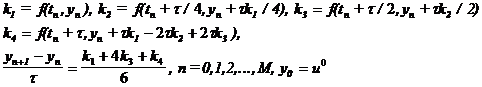
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.