Практическая работа 19. Тема «Определение промежутков возрастания и убывания функций, нахождение экстремумов функции». Материал к практической работе

Практическая работа 19

Тема «Определение промежутков возрастания и убывания функций, нахождение экстремумов функции»

Цель работы:умение находить область определения и множество значений функции, промежутки знакопостоянства, определять наибольшее (наименьшее) значение функции на отрезке, промежутки возрастания и убывания функции, находить экстремумы функции.

Ход работы:

1. Повторить материалы лекции 18 - 20.

2. Изучить материал к практической работе.

3. Выполнить задания практической работы.

Материал к практической работе

На рисунке изображен график некоторой функции у = f(х), с помощью которого можно описать ее свойства.

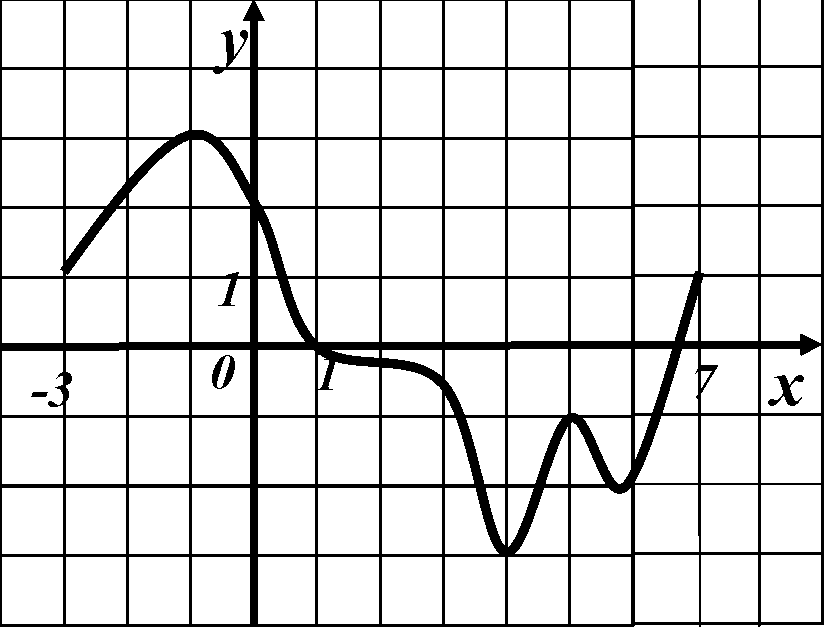
1. Область определения данной функции (смотрим по оси Ох) - отрезок [-3; 7]. Поэтому можно записать, что D(f) = [-3; 7].

2. Множество значений функции (смотрим по оси Оу) – отрезок [-3; 3]. Поэтому можно записать, что Е(f) = [-3; 3].

3. Нули функции – точки, в которых функция обращается в нуль. Эти точки являются решениями уравнения f(х) = 0. Геометрически (на графике) – это абсциссы точек пересечения графика функции с осью Ох.

Получаем, что нули функции – это х₁ = 1 и х₂ = 6,7 (это значение определяем приблизительно по графику и точное – решая уравнение).

4. Промежутки знакопостоянства – это промежутки постоянного знака – множество решений неравенств f(х) > 0 и f(х) < 0. Геометрически – это интервалы оси Ох, соответствующие точкам графика, лежащим выше (или ниже) этой оси.

В нашем случае f(х) > 0: [-3;1) (6,7; 7] и f(х) < 0: (1; 6,7).

5. Промежутки монотонности – промежутки оси Ох, на которых функция возрастает (промежутки возрастания) или убывает (промежутки убывания). Геометрически – это интервалы оси Ох, где график функции идет вверх или вниз.

Получаем, что функция f(х) возрастает на промежутках (-3; -1) (4; 5) (5,7; 7) и убывает на промежутках (-1; 4) (5; 5,7).

Записываем: f(х) 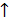: (-3; -1) (4; 5) (5,7; 7);

f(х) 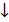: (-1; 4) (5; 5,7).

6. Точки экстремума – точки, лежащие внутри области определения, в которых функция принимает самое большое (максимум) или самое малое (минимум) значения по сравнению со значениями в близких точках. Геометрически – около точек экстремума график функции выгибается выпуклостью вверх или вниз.

В нашем случае точками экстремума являются (-1; 3) и (5; -1) – максимум,

(4; -3) и (5,7; -2) – минимум.

Записываем: х_max: -1 и 5; х_min: 4 и 5,7.

7. Наибольшее и наименьшее значение функции на заданной области определения – в точке х₀ функция f(х) принимает наибольшее (наименьшее) значение,

если f(x₀) 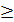f(x) ( f(x₀) 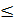f(x) ) для любого значения х. само число х₀ – наибольшее (наименьшее) значение функции. Геометрически – это ординаты самой высокой (самой низкой) точки графика.

В нашем случае это точки у = 3 – наибольшее значение функции, а у = -3 – наименьшее значение функции на области определения [- 3; 7 ].

Записываем: у_наиб = 3 и у_наим = - 3.

Схема исследования функции:

1. Область определения функции.

2. Множество значений функции.

3. Нули функции.

4. Промежутки знакопостоянства.

5. Промежутки монотонности.

6. Точки экстремума.

7. Наибольшее и наименьшее значение функции на заданной области определения.

Практический материал

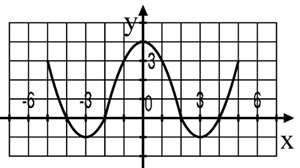
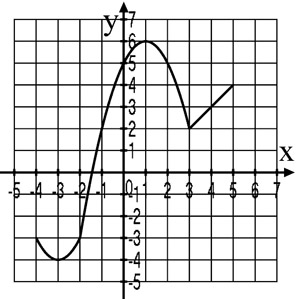
1.Выполните исследование заданных на графиках некоторых функций, пользуясь схемой:

А)

Б)