Внешнее представление исходных данных

Министерство образования и науки Российской Федерации

НГТУ

Кафедра Прикладной математики

Лабораторная работа №3

По “Практикум на ЭВМ: Структуры данных и алгоритмы”

Факультет прикладной математики и информатики

Группа ПМ-01

Студент: Курочкин А. В.

Преподаватель: Еланцева И. Л.

Новосибирск

1. Условие задачи.

Задано бинарное дерево. Определить, есть ли в этом дереве хотя бы два одинаковых элемента.

2. Анализ задачи.

Дано:

A={(a_i,(A)|0,(A)|0}, i 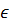N, a_i – символ

Результат:

B 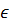{1,0}

Решение:

При tr1=u, s1=NULL, step1=0

Повторять

tr2=U, s2=NULL, step2=0

Повторять

Если tr1->chaar=tr2->chaar и step1≠step2, то flag=1

Если tr2->left≠NULL и tr2->right≠NULL, то tr2->right в стек2

Иначе

Если tr2->left=NULL и tr2->right=NULL, то tr2->right из стека2

Иначе

Если tr2->left≠NULL, то tr2=tr2->left

Иначе tr2=tr2->right

step2=step2+1

пока tr2≠NULL и flag≠1

Если tr1->left≠NULL и tr1->right≠NULL, то tr1->right в стек1

Иначе

Если tr1->left=NULL и tr1->right=NULL, то tr1->right из стека1

Иначе

Если tr1->left≠NULL, то tr1=tr1->left

Иначе tr1=tr1->right

Step1=step1+1

пока tr1≠NULL и flag≠1

3. Структуры данных.

3.1 Внешнее представление исходных данных

{(a_i,(A)|0,(A)|0}, i 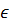N – дерево (списочная запись)

3.2 Внешнее представление результатов

1/0 - имеются/не имеются

3.3 Внутреннее представление исходных данных.

Бинарное динамическое дерево – иерархический нелинейный однонаправленный список без заглавного звена.

Элемент дерева:

tr{char chaar; tr* left; tr* right;} s – значение символьной переменной

left – указатель на левое поддерево

right – указатель на правое поддерево

Для обхода дерева используется стек - линейный ациклический однонаправленный список (функции, с ним связанные, описаны в отчёте по лабораторной работе №2)

Элемент списка:

typest{char el; typest *next;}

hs – указатель на линейный ациклический однонаправленный список

p – указатель на формируемое поддерево

U – указатель на дерево

t – элемент, извлекаемый из линейного ациклического однонаправленного списка

3.4 Внутреннее представление результатов.

flag – переменная, отражающая наличие/отсутствие одинаковых элементов в дереве

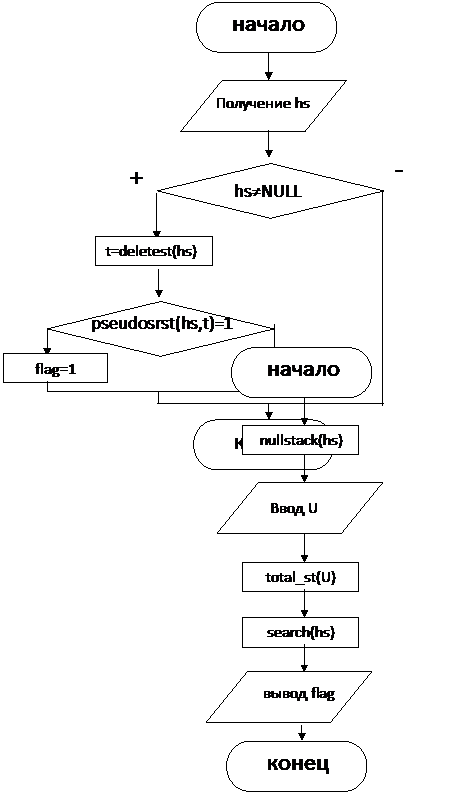
4. Схема алгоритма решения.

total_sr(s1) – помещение всех элементов дерева в стек

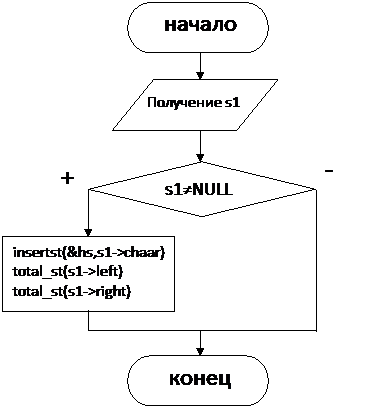search(hs) – поиск повторного вхождения первого элемента в стеке

5. Текст программы.

stack.h

struct typest{char el; typest *next;} *hs;

int *ins;

void nullstack(typest *hs)

{

hs=NULL;

}

int reconst(typest *hs)

{

if(hs==NULL)

return 0;

else

return 1;

}

void insertst(typest **hs,char elem)

{

typest *s=new typest;

s->el=elem;

s->next=*hs;

*hs=s;

}

char deletest(typest **hs)

{

char bor=(*hs)->el;

typest *del=*hs;

*hs=(*hs)->next;

delete del;

return bor;

}

void seest(typest *hs)

{

if(hs!=NULL)

{

typest *tempst=NULL;

while(hs!=NULL)

{

insertst(&tempst,deletest(&hs));

printf("%c ",tempst->el);

}

while(tempst!=NULL)

{

insertst(&hs,deletest(&tempst));

}

else printf("the stack is empty");

printf("\n");

}

int pseudosrst(typest *ps, char element)

{

while(ps!=NULL)

{

if(ps->el==element)

return 1;

ps=ps->next;

}

return 0;

}

lab020301

#include <stdio.h>

#include "stack.h"

struct tr{char chaar; tr* left; tr* right;} *U;

int flag=0;

tr* build()

{

char c;

tr *p;

scanf("%c",&c);

switch(c)

{

case '(':

{

p=new tr;

scanf("%c",&c);

p->chaar=c;

p->left=build();

p->right=build();

scanf("%c",&c);

return p;

}

case '0':

return NULL;

case ',':

p=build();

break;

}

void total_st(tr *s1)

{

if(s1!=NULL)

{

insertst(&hs,s1->chaar);

total_st(s1->left);

total_st(s1->right);

}

void search(typest *hs)

{

while(hs!=NULL)

{

char t=deletest(&hs);

if(pseudosrst(hs,t)==1)

flag=1;

}

int main()

{

nullstack(hs);

U=build();

total_st(U);

search(hs);

printf("%d",flag);

return 0;

}

6. Тесты.

№	Дано n, (A)	Результат	Примечание
	(A,(A,0,0),0)		Тривиальная задача
	(j,(8,(*,0,0),(=,0,0)),(G,0,(x,0,0)))		Одинаковых элементов не существует
	(6,(9,0,0),(9,0,0))		Разные поддеревья.
			Пустое дерево
	(9,0,0)		Дерево только с одним элементом

7. Результаты.

Результаты тестов соответствуют ожидаемым, что показывает корректность программы решения задачи.