
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие № 25. Методические рекомендации
Практическое занятие № 25
Тема:Применение комплексных чисел в электротехнических расчетах.
Цель:научиться решать задачи на расчёты электрических цепей
Методические рекомендации
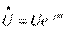
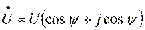
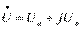
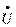
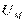
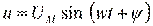 Напряжение и ток. Имеется уравнение . В электротехнике за длину вектора берется не максимальное, а действующее значение. Оно обозначается большой буквой U без индекса и вычисляется путем деления максимального значения на
Напряжение и ток. Имеется уравнение . В электротехнике за длину вектора берется не максимальное, а действующее значение. Оно обозначается большой буквой U без индекса и вычисляется путем деления максимального значения на 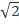 . Синусоидальная величина, выраженная комплексным числом, называется комплексом и обозначается прописной буквой с точкой наверху . Комплекс напряжения можно написать в трех формах алгебраической –
. Синусоидальная величина, выраженная комплексным числом, называется комплексом и обозначается прописной буквой с точкой наверху . Комплекс напряжения можно написать в трех формах алгебраической –
тригонометрической – и показательной –
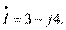
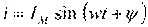
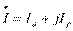 Таким образом, в комплексе напряжения модуль равен действующему значению, аргумент – начальному фазовому углу, активная составляющая – вещественной части комплекса напряжения, реактивная – мнимой части. Аналогично для тока: ; ….
Таким образом, в комплексе напряжения модуль равен действующему значению, аргумент – начальному фазовому углу, активная составляющая – вещественной части комплекса напряжения, реактивная – мнимой части. Аналогично для тока: ; ….
Задача 1. Дано: ток в комплексной форме Написать уравнение тока.
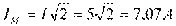
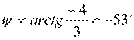
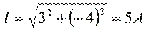 Решение. Для того чтобы написать уравнение, надо знать амплитуду и начальный фазовый угол. Поэтому надо найти модуль – действующее значение и аргумент – начальный фазовый угол заданного комплекса тока:
Решение. Для того чтобы написать уравнение, надо знать амплитуду и начальный фазовый угол. Поэтому надо найти модуль – действующее значение и аргумент – начальный фазовый угол заданного комплекса тока:
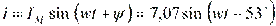 |
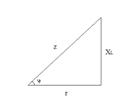
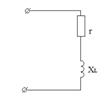
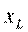
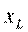
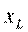 Сопротивление и проводимость. Имеется цепь (рис. 1): r – активное сопротивление (лампа накаливания); – индуктивное сопротивление (катушка); z – общее сопротивление цепи, называемое полным.
Сопротивление и проводимость. Имеется цепь (рис. 1): r – активное сопротивление (лампа накаливания); – индуктивное сопротивление (катушка); z – общее сопротивление цепи, называемое полным.
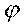 Рис.1 Рис.2 Сопротивления r, , z образуют прямоугольный треугольник сопротивления (рис. 2). Угол – угол сдвига фаз. Сопротивления не являются синусоидальными величинами, однако отрезок z может быть выражен комплексным числом, считая, что отрезок r откладывается по оси вещественных чисел, а отрезок – по оси мнимых чисел. Сопротивление в комплексной форме обозначается буквой Z.
Рис.1 Рис.2 Сопротивления r, , z образуют прямоугольный треугольник сопротивления (рис. 2). Угол – угол сдвига фаз. Сопротивления не являются синусоидальными величинами, однако отрезок z может быть выражен комплексным числом, считая, что отрезок r откладывается по оси вещественных чисел, а отрезок – по оси мнимых чисел. Сопротивление в комплексной форме обозначается буквой Z.
Задача 2
Определить ток 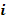 в неразветвленной части, если токи в ветвях:
в неразветвленной части, если токи в ветвях:
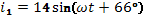
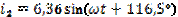
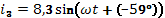
Дано:
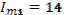 ,
, 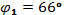
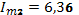 ,
, 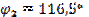
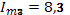 ,
, 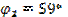
Решение:
Найдем: 1. Комплексные токи в цепях: 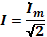
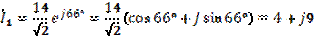 (А)
(А)
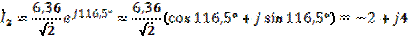 (А)
(А)
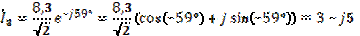 (А)
(А)
2. Комплекс тока в неразветвленной части цепи: 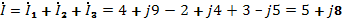
3.Модуль тока: 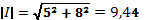 (А)
(А)
4.Аргумент через 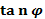 :
: 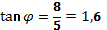 ,
, 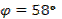
Ответ: 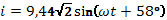
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|