
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Выведем основное логарифмическое тождество: а log a b = b
Тема сегодняшнего урока - Логарифм и их свойства (откройте тетради и запишите дату и тему).
На этом уроке мы познакомимся с понятием «логарифм», также рассмотрим свойства логарифмов. Тема эта актуальна, т.к. логарифм всегда встречается на итоговой аттестации по математике.
Зададим вопрос:
1) В какую степень нужно возвести 3, чтобы получить 9? Очевидно, во вторую. Показатель степени, в которую нужно возвести число 3, чтобы получить 9, равен 2.
2) В какую степень нужно возвести 2, чтобы получить 8? Очевидно, во вторую. Показатель степени, в которую нужно возвести число 2, чтобы получить 8, равен 3.
Во всех случаях мы искали показатель степени, в которую нужно что-то возвести, чтобы что-то получить. Показатель степени, в которую нужно что-то возвести называется логарифмом и обозначается log.
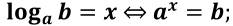
Число, которое мы возводим в степень, т.е. основание степени, называется основанием логарифма и записывается в нижнем индексе. Затем пишется число, которое мы получает, т.е. число, которое мы ищем: log3 9=2
Эта запись читается так: «Логарифм числа 9 по основанию 3». Логарифм числа 9 по основанию 3 это показатель степени, в которую нужно возвести 3, чтобы получить 9. этот показатель равен 2.
Дадим определение логарифма.
Определение. Логарифмом числа b>0 по основанию a>0, a ≠ 1 называется показатель степени, в которую надо возвести число a, чтобы получить число b.
Логарифмом числа b по основанию a обозначаетсяloga b.
История возникновения логарифма:
Логарифмы были введены шотландским математиком Джоном Непером (1550-1617) и математиком Иостом Бюрги (1552-1632).
Бюрги пришел к логарифмам раньше, но опубликовал свои таблицы с опозданием (в 1620г.), а первой в 1614г. появилась работа Непера «Описание удивительной таблицы логарифмов».
С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.
Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку.
Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры. Теперь ее вытеснили калькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни микрокалькуляторы.
Рассмотрим примеры:
log327=3; log525=2; log255=1/2; log5 1/125=-3; log-2-8- не существует; log51=0; log44=1
Рассмотрим такие примеры:
10. loga1=0, а>0, a ≠ 1;
20. logaа=1, а>0, a ≠ 1.
Эти две формулы являются свойствами логарифма. Запишите свойства и их необходимо запомнить.
В математике принято следующее сокращение:
log10а= lg а- десятичный логарифм числа а (буква «о» пропускается, а основание 10 не ставят).
logеа= ln а - натуральный логарифм числа а. «е» - это такое иррациональное число, равное » 2,7 (буква «о» пропускается, а основание «е» не ставят).
Рассмотрим примеры:
lg 10=1; lg 1=0
ln e=1 ; ln 1=0 .
Как перейти из логарифмического равенства к показательному: logаb=с, с – это логарифм, показатель степени, в которую нужно возвести а, чтобы получить b. Следовательно, а степени с равен b: а с= b.
Рассмотрим пять логарифмических равенств. Задание: проверить их правильность. Среди этих примеров есть ошибки. Для проверки воспользуемся данной схемой.
• lg 1 = 2 (10 2=100)- это равенство не верное.
• log1/2 4 = 2- это равенство не верное.
• log31=1 - это равенство не верное.
• log1/3 9 = -2 - это равенство верное.
• log416 = -2- это равенство не верное.
Выведем основное логарифмическое тождество: а log a b = b
Рассмотрим пример.
5 log 5 13 =13
Свойства логарифмов:
3°. logа ху = logах + logау.
4°. logа х/у = logах - logау.
5°. logах p = p · logах, для любого действительного p.
Рассмотрим пример на проверку 3 свойства:
log28 + log232= log2 8∙32= log2 256=8
3 +5 = 8
Рассмотрим пример на проверку 5 свойства:
3∙ log28= log283= log2512 =9
3∙3 = 9
Формула перехода от одного основания логарифма к другому основанию:
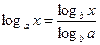 |
Эта формула потребуется при вычислении логарифма по калькулятору.
Возьмем пример: log3 7 = lg7 / lg3. В калькуляторе можно вычислить только десятичный и натуральный логарифм. Вводим цифру 7 и нажмем кнопку «лог», также вводим цифру 3 и нажмем кнопку «лог», делим верхнее значение на нижнее и получаем ответ.
- Закрепление.
Для закрепления новой темы решим примеры.
Пример 1. Назовите свойство, которое применяется при вычислении следующих логарифмов, и вычислите (устно):
• log66
• log 0,51
• log63+ log62
• log36- log32
• log448
Пример 2.
Перед вами 8 решённых примеров, среди которых есть правильные, остальные с ошибкой. Определите верное равенство (назовите его номер), в остальных исправьте ошибки.
- log232+ log22= log264=6
- log553 = 2;
- log345 - log35 = log340
- 3∙log24 = log2 (4∙3)
- log315 + log33 = log345;
- 2∙log56 = log512
- 3∙log23 = log227
- log2162 = 8.
- самостоятельная работа.
Вычислите:
1) log416
2) log25125
3) log82
4) log66
Вычислите:
1) log327
2) log4 8
3) log49 7
4) log55
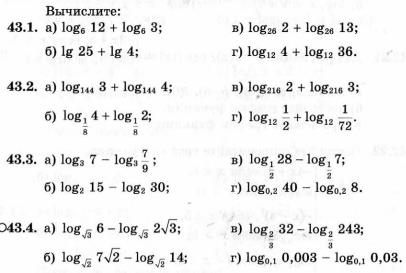
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|