
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задачи средствами MS Excel
Тема «Определение кратчайшего расстояния между пунктами по их географическим координатам»
1. Постановка задачи.
Для вычисления кратчайшего расстояния необходимо определить географические координаты начального и конечного пунктов.
Для определения географических координат пунктов лучше использовать карты, составленные в нормальных конических и цилиндрических, а также поперечных азимутальных проекциях, равнопромежуточных по меридианам.
2. Разработка модели.
Определение длин линий без их непосредственного измерения на картах производится по формулам сферической тригонометрии:
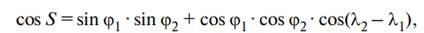
где S – расстояние, выраженное в градусной мере;
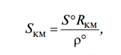 φ1 и φ 2, λ1 и λ2 – географические координаты начального и конечного пунктов.
φ1 и φ 2, λ1 и λ2 – географические координаты начального и конечного пунктов.
Для получения результата в километрах используется формула
 где R – радиус кривизны для средней широты
где R – радиус кривизны для средней широты
|
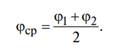 Средняя широта
Средняя широта
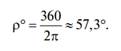
Значение радиана
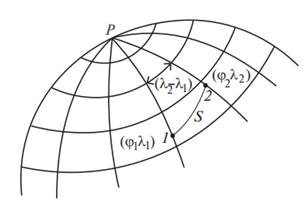
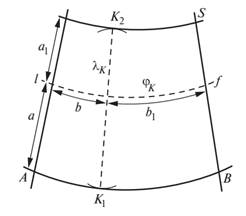
Для вычисления географических координат φK и λK определяют частоту градусной сетки (Δϕ, Δλ) и с помощью измерителя и поперечного масштаба измеряют отрезки a, a1, b и b1 (рис. 2).
|
Вычисления координат выполняют по следующим формулам:
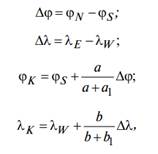 где φN и φS – широта северной и южной параллели трапеции
где φN и φS – широта северной и южной параллели трапеции
λE и λW – долгота восточного и западного меридиана трапеции.
Результаты вычисления координат пункта K можно проконтролировать по формулам:
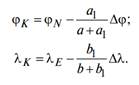
3. Решение задачи средствами MS Excel
Задача: Определите кратчайшее расстояние между городами Минск и Чикаго и вычислите относительную погрешность измерения этого расстояния по прямой на «Политической карте мира» («Географический атлас для учителей средней школы»).
1. Откройте табличный процессор в Microsoft Excel.
2. Создайте таблицу по образцу:
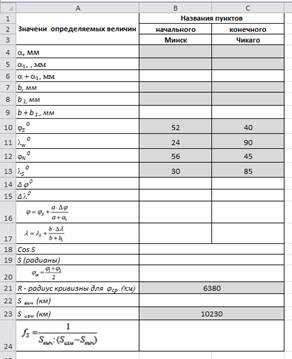
- Для определения географических координат Минска и Чикаго используются построенные в нормальных конических проекциях карты.
В трапециях с городами Минск и Чикаго требуется провести меридианы и параллели через эти города.
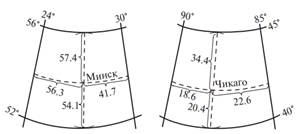
С помощью поперечного масштаба (в миллиметрах) измеряются отрезки а и а1, b и b1 (рис. 3):
Минск: а = 54,1 мм; а1= 57,4 мм; b = 56,3 мм; b1 = 41,7 мм;
Чикаго: а = 20,4 мм; а1 = 34,4 мм; b = 18,6 мм; b1 = 22,6 мм.
|
4. Внесите значения а и а1, b и b1 для Минска и Чикаго в таблицу.
5. Математические расчеты при выполнении данной работы целесообразно производить в Microsoft Excel. по формулам:
B6 =СУММ(B4:B5)
C6 =СУММ(C4:C5)
B9 =СУММ(B7:B8)
C9 =СУММ(C7:C8)
B14 =B12-B10
C14 =C12-C10
B15 =B13-B11
C15 =C13-C11
B16 =B10+(B4*B14)/B6
C16 =C10+(C4*C14)/C6
B17 =B11+(B7*B15)/B9
C17 =ЗНАК(-1)*(C11+(C7*C15)/C9)
BC18 =SIN(РАДИАНЫ(B16))*SIN(РАДИАНЫ(C16))+COS(РАДИАНЫ(B16))* COS(РАДИАНЫ(C16))*COS(РАДИАНЫ(B17-C17))
BC19 =ACOS(B18)
BC20 =(B16+C16)/2
BC22 =B19*B21
BC24 =1/(B22/(B23-B22)).
6. Результат выполненной работы:
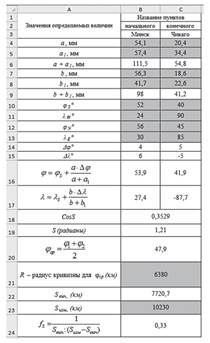
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|