
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства бинома и биномиальных коэффициентов
Биномом Ньютона называют разложение вида:
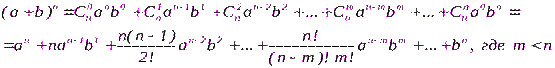
Цель изучения бинома Ньютона – упрощение вычислительных действий.
· правая часть формулы – разложение бинома;
· 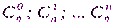
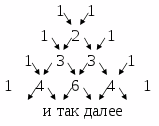 – биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
– биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Свойства бинома и биномиальных коэффициентов
1. 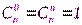
2. Число всех членов разложения на единицу больше показателя степени бинома, то есть равно 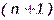
3. Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома, то есть n
Типовые задачи по теме «Бином Ньютона»
1. Найти член (номер члена) разложения бинома
2. Вывести бином по известным членам разложения (по известной сумме)
3. Вычислить сумму биномиальных коэффициентов разложения бинома
и другие
Избавьтесь от скобок:
а) (x+2)6;
б) (3x+2y)4;
в) (2z−2t)8;
г) (x−4y)5.
задание 1.Изобразите треугольник Паскаля, содержащий 11 строк.
Задание 2.Представить выражение в виде многочлена.
1. (а +2)5. 2. 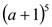 . 3.
. 3. 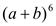 .
.
4. 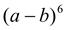 . 5. (а - 2)5. 6.
. 5. (а - 2)5. 6. 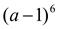 .
.
7. 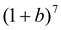 . 8.
. 8. 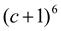 . 9. (с + 2)5 .
. 9. (с + 2)5 .
10. (а +3)5 . 11. 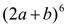 . 12.
. 12. 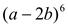 .
.
13. 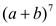 . 14.
. 14. 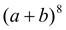 . 15.
. 15. 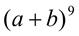 .
.
16. (с + 2)5. 17. 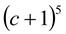 . 18.
. 18. 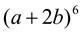 .
.
19. 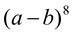 . 20. (3а + 2)5. 21.
. 20. (3а + 2)5. 21. 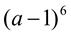 .
.
22. 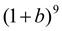 . 23.
. 23. 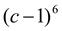 . 24. (с + 3)5 .
. 24. (с + 3)5 .
25. 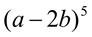 .
.
Задание 3.Вычислить значения выражений.
1. 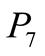 ;
; 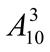 ;
; 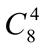 . 2.
. 2. 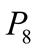 ;
; 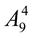 +
+ 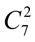 .
.
3. 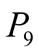 ;
; 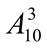 +
+ 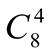 .
.
4. 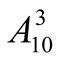 +
+  . 5.
. 5. 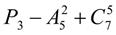 ; 6.
; 6. 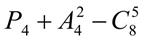 .
.
7. 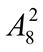 +
+ 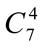 . 8.
. 8. 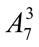 +
+ 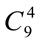 . 9.
. 9. 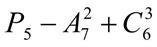 .
.
10. 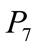 +
+ 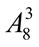 +
+ 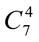 . 11.
. 11. 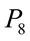 +
+ 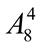 +
+ 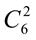 . 12.
. 12. 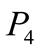 +
+ 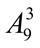 +
+ 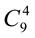 .
.
13. 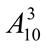 +
+ 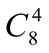 . 14.
. 14. 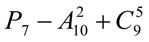 ; 15.
; 15. 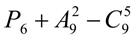 .
.
16. 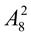 +
+ 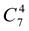 . 17.
. 17. 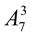 +
+ 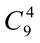 . 18.
. 18. 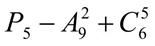 .
.
19. 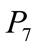 +
+ 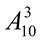 +
+ 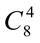 . 20.
. 20. 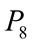 +
+ 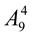 +
+ 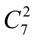 . 21.
. 21. 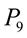 +
+ 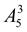 +
+ 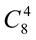 .
.
22. 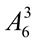 +
+ 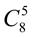 . 23.
. 23. 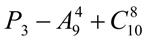 ; 24.
; 24. 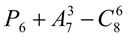 .
.
25. 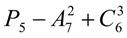 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|