Задача 2.

Примеры решения задач

Задача 1. Шарик радиусом r катится со скоростью υ0 по двум рельсам, расположенным на расстоянии 2а друг от друга. Определите скорости точек А и В относительно рельсов (рис. 1.66, а).

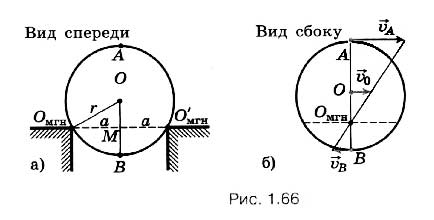
Р е ш е н и е. Мгновенная ось вращения О_мгн в данном случае показана на рисунке 1.66, б. Угловая скорость поворота шарика относительно этой оси ω = υ0/OM, где

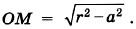
Отсюда

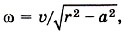
Следовательно,

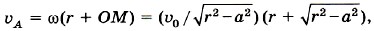
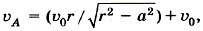
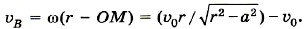
Задача 2.

Чему равен максимальный угол наклона плоскости к горизонту, если на этой плоскости удерживается груз? Коэффициент трения между грузом и плоскостью равен 0,413. Ответ дать в градусах.

ДАНО:

μ=0.413μ=0.413

Найти:

α_max

РЕШЕНИЕ:

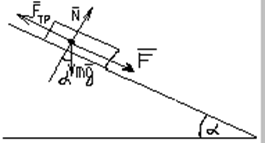
Так как груз по плоскости не движется, то его ускорения равняется нулю. А значит, по второму закону Ньютона, проекция силы тяжести на линию движения, запишется так:

F=m∗g∗sin(α)F=m∗g∗sin(α)

Эта проекция меньше силы трения:

Ftr=μ∗N=μ∗m∗g∗cos(α)Ftr=μ∗N=μ∗m∗g∗cos(α)

А значит, можем получить отношение, а затем выразить из него искомую величину - максимальный угол удержания груза:

sin(αmax)=μ∗cos(αmax)sin(αmax)=μ∗cos(αmax)

αmax=atan(μ)αmax=atan(μ)

Подставим числовое значение и получим ответ:

αmax=22.44∘

Задача 3.
Шар массой13 кг подвешен на нити к подставке, которая укреплена на тележке. Тележка скатывается без трения с наклонной плоскости, угол наклона плоскости к горизонту 53 град. Чему равно натяжение нити?

ДАНО:

m = 13 кг

α = 53 °

Найти T

РЕШЕНИЕ:

Т.к тележка скатывается без трения, то нить будет перпендикулярна наклонной плоскости, поэтому проекции сил на ось параллельно нити будут равны.

T=mg⋅cos(α) ускорение свободного падение g = 9.832 м/с²

Подставляя значения из дано в формулу, находим ответ: T =76,922 Н

12 Следующая ⇒