- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица № 1. Исходные данные
Задача 1
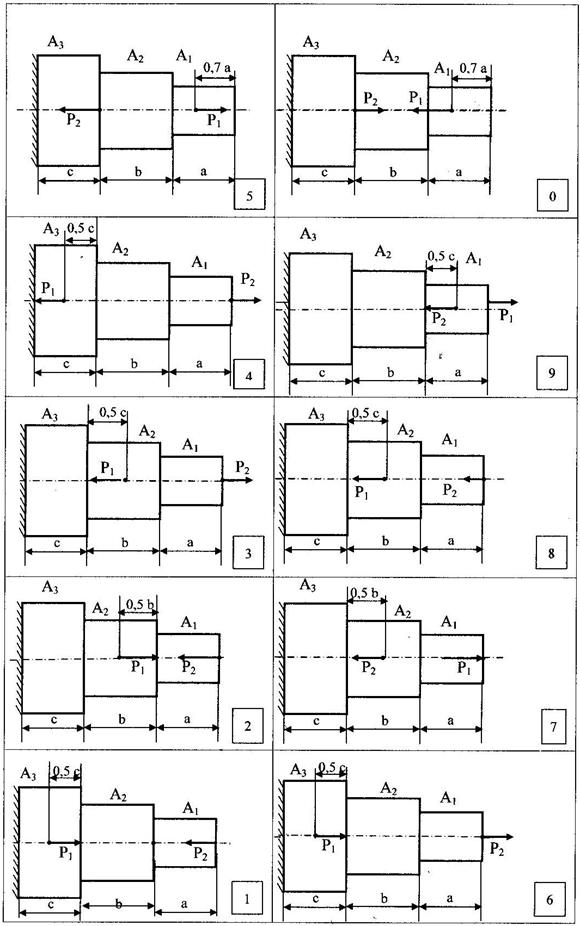
Невесомый стержень переменного сечения и площадями А1, А2, А3 и длиной участков а, b, с, жёстко защемлённый с одной стороны, находится под действием сил Р1 и Р2 . Модуль упругости 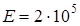 МПа.
МПа.
ТРЕБУЕТСЯ:
1. Сделать чертёж стержня по заданным размерам в масштабе (соотношение размеров А1, А2, А2 на рисунке может не соответствовать заданию);
2. Составить для каждого участка бруса в сечении аналитические выражения изменения продольного усилия 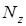 , напряжений
, напряжений 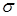 и перемещений поперечных сечений бруса
и перемещений поперечных сечений бруса 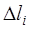 ;
;
3. Построить эпюры продольных усилия 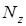 , напряжений
, напряжений 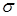 и перемещений поперечных сечений бруса
и перемещений поперечных сечений бруса 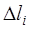 ;
;
4. Сделать вывод о прочности стержня при 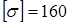 МПа.
МПа.
Исходные данные к задаче
| № строки | Схема по рис. | Р1, кН | Р2, кН | A1, см2 | A2, см2 | A3, см2 | а, м | b, м | c, м |
| 2,1 | 2,1 | 2,1 | 0,5 | 0,5 | 0,5 | ||||
| 2,2 | 2,2 | 2,2 | 0,6 | 0,6 | 0,6 | ||||
| 2,3 | 2,3 | 2,3 | 0,7 | 0,7 | 0,7 | ||||
| 2,4 | 2,4 | 2,4 | 0,8 | 0,8 | 0,8 | ||||
| 2,5 | 2,5 | 2,5 | 0,4 | 0,4 | 0,4 | ||||
| 2,6 | 2,6 | 2,6 | 0,3 | 0,3 | 0,3 | ||||
| 2,7 | 2,7 | 2,7 | 0,5 | 0,5 | 0,5 | ||||
| 2,8 | 2,8 | 2,8 | 0,6 | 0,6 | 0,6 | ||||
| 2,9 | 2,9 | 2,9 | 0,7 | 0,7 | 0,7 | ||||
| 2,0 | 2,0 | 2,0 | 0,8 | 0,8 | 0,8 | ||||
| в | б | в | а | б | в | а | б | в |
Пример
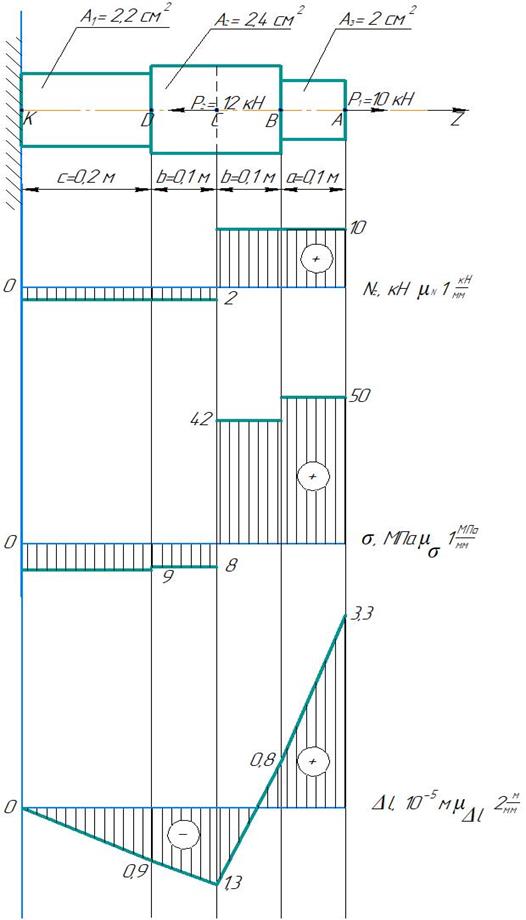
Невесомый стержень переменного сечения и площадями 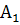 ,
, 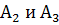 жестко закрепленный на конце, находится под действием
жестко закрепленный на конце, находится под действием 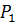 и
и 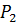 . Модуль упругости Е=2∙
. Модуль упругости Е=2∙ 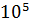 МПа.
МПа.
Требуется:
1. Сделать чертеж стержня по заданным размерам в масштабе;
2. Составить для каждого участка бруса в сечении аналитические выражения изменения продольного усилия 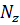 , напряжений σ и перемещений поперечных сечений бруса ∆
, напряжений σ и перемещений поперечных сечений бруса ∆ 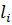 ;
;
3. Построить эпюры для продольного усилия 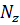 , напряжений σ и перемещений поперечных сечений бруса ∆
, напряжений σ и перемещений поперечных сечений бруса ∆ 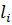 ;
;
4. Сделать вывод о прочности стрежня при [σ]=160 МПа;
Исходные данные:
| P1, кН | P2, кН | a, м | b, м | c, м | A1, см2 | A2, см2 | A3, см2 | [σ], МПа | E, МПа |
| 0,1 | 0,2 | 0,2 | 2,2 | 2,4 | 2∙105 |
Решение:
1) Составим для каждого участка бруса в сечении аналитические выражения изменения продольного усилия 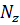 и найдем их:
и найдем их:
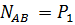 = 10 кН
= 10 кН
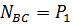 = 10кН;
= 10кН;
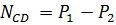 = 10
= 10 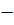 12 =
12 = 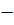 2кН;
2кН;
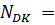
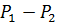 =
= 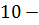 12 =
12 = 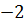 кН;
кН;
2) Составим для каждого участка бруса в сечении аналитические выражения изменения напряжений σ и найдем их: 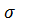 =
= 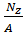 ;
;
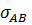 =
= 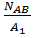 =
= 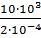 =50 МПа;
=50 МПа;
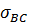 =
= 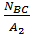 =
= 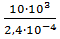 =
=  MПа;
MПа;
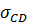 =
= 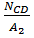 =
= 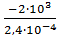 =
= 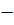 8 MПа;
8 MПа;
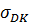 =
= 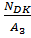 =
= 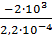 =
= 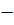 9 MПа;
9 MПа;
3)Составим для каждого участка бруса в сечении аналитические выражения изменения перемещений поперечных сечений бруса ∆ 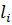 .
.
δ 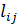 =
= 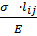 ;
;
δ 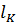 = 0 м;
= 0 м;
δ 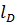 = δ
= δ 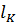 + δ
+ δ 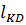 = δ
= δ 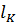 +
+ 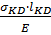 = 0
= 0 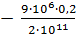 =
= 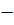 0,9
0,9 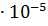 м;
м;
δ 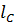 = δ
= δ 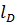 + δ
+ δ 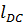 = δ
= δ 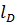 +
+ 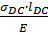 =
= 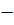 0,9
0,9 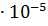
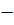
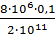 =
= 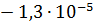 м;
м;
δ 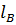 = δ
= δ 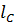 + δ
+ δ 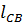 = δ
= δ 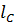 +
+ 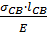 =
= 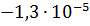
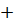
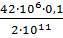 =
= 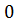 ,8
,8 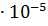 м;
м;
δ 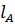 = δ
= δ 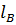 + δ
+ δ 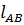 = δ
= δ 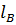 +
+ 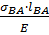 =
= 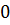 ,8
,8 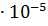 м
м 
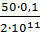 =
= 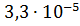 м;
м;
4) Проверим прочность стержня при допускаемом напряжении 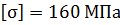
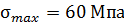 ;
; 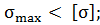
Допустимая недогрузка 20%
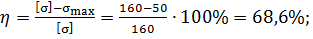
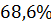 >20% прочность бруса не обеспечена.
>20% прочность бруса не обеспечена.
Задача 2
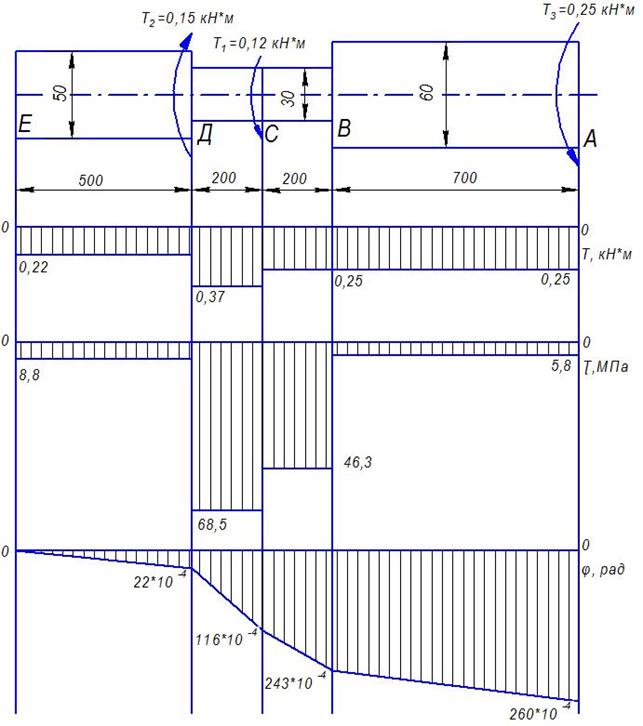
К стальному валу приложены три известных момента: Т1, Т2,Т3. Модуль сдвига 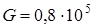 МПа.
МПа.
ТРЕБУЕТСЯ:
1. Сделать чертёж вала по заданным размерам в масштабе (соотношение размеров d1, d2, d3 на рисунке может не соответствовать рисунку вала задания);
2. Построить эпюру крутящих моментов Т;
3. Построить эпюру касательных напряжений 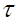 ;
;
4. Построить эпюру углов закручивания 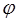 ;
;
5. Сделать вывод о прочности стержня при 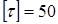 МПа.
МПа.
Исходные данные к задаче
| № строки | Схема по рис. | Т1, кН.м | Т2, кН.м | Т3, кН.м | d1, мм | d2, мм | d3, мм | a мм | b мм | c мм |
| 0,11 | 0,11 | 0,21 | ||||||||
| 0,12 | 0,12 | 0,22 | ||||||||
| 0,13 | 0,13 | 0,23 | ||||||||
| 0,14 | 0,14 | 0,24 | ||||||||
| 0,15 | 0,15 | 0,25 | ||||||||
| 0,16 | 0,16 | 0,26 | ||||||||
| 0,17 | 0,17 | 0,27 | ||||||||
| 0,18 | 0,18 | 0,28 | ||||||||
| 0,19 | 0,19 | 0,29 | ||||||||
| 0,20 | 0,20 | 0,3 | ||||||||
| в | б | в | а | б | в | а | б | в |
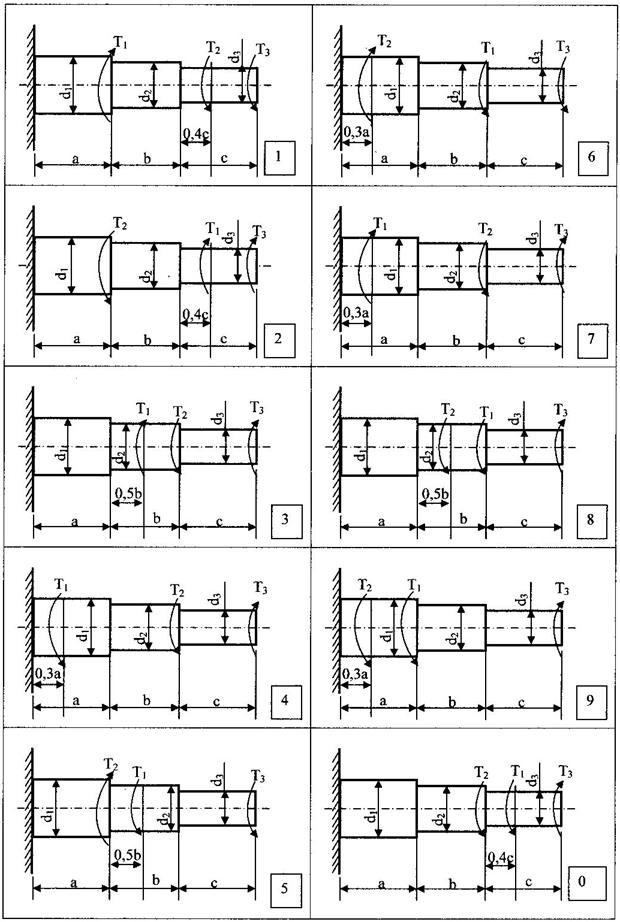
Пример
К стальному валу приложены три известных момента T1, T2 и T3. Модуль сдвига 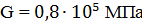
ТРЕБУЕТСЯ:
1. Сделать чертеж вала по заданным размерам в масштабе;
2. Построить эпюру крутящих моментов Т;
3. Построить эпюру касательных напряжений τ;
4. Построить эпюру углов закручивания φ;
5. Сделать вывод о прочности стержня при [τ]=50 МПа.
Исходные данные:
| T1 кН∙м | T2 кН∙м | T3 кН∙м | a, м | b, м | c, м | d1, м | d2, м | d3, м | [τ], МПа |
| 0,12 | 0,15 | 0,25 | 0,5 | 0,4 | 0,7 | 0,05 | 0,03 | 0,06 |
Решение:
1) Построение эпюры крутящих моментов
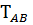 =
= 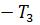 =
=  –0,25 кН∙м
–0,25 кН∙м
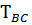 =
= 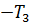 = –0,25 кН∙м
= –0,25 кН∙м
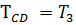
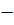
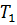 =
= 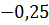
 0,12 = –0,37 кН∙м
0,12 = –0,37 кН∙м
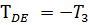
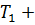
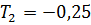
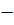 0,12
0,12 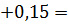
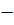 0,22 кН∙м
0,22 кН∙м
2) Построение эпюры касательных напряжений
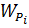 =
= 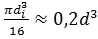 ; τ =
; τ = 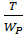 ;
;
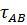 =
= 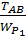 =
= 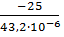 =
= 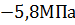 ;
;
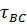 =
= 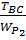 =
= 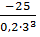 =
= 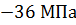 ;
;
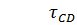 =
= 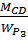 =
= 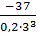 = – 68,5
= – 68,5 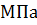 ;;
;;
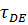 =
= 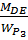 =
= 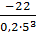 =
= 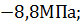
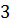 ) Проверка прочности вала
) Проверка прочности вала
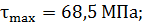
[τ]=50 МПа
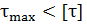 -Перегрузка
-Перегрузка
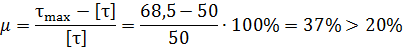
Следовательно, условие прочности не выполняется.
4) Построение эпюры углов поворота поперечных сечений
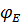 =0;
=0;
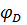 =
= 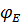 +
+ 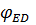 =
= 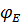 +
+ 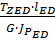 = 0 +
= 0 + 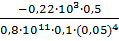 =
= 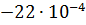 рад;
рад;
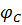 =
= 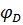 +
+ 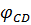 =
= 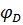 +
+ 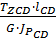 =
= 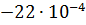 +
+ 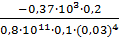 =
= 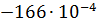 рад;
рад;
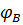 =
= 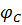 +
+ 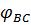 =
= 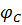 +
+ 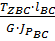 =
= 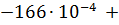
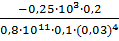 =
= 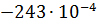 рад;
рад;
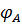 =
= 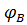 +
+ 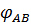 =
= 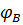 +
+ 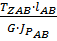 =
= 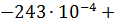
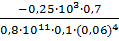 =
= 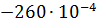 рад;
рад;
Задача 3
Построение эпюр внутренних усилий в статически определимых балках
Для заданной балки требуется:
1. Написать выражения поперечной силы Qy и изгибающего момента Мx для каждого участка в общем виде;
2. Построить эпюры поперечной силы Qy и изгибающего момента Мx.
Исходные данные к задаче
| № строки | Схема по рис. | Р, кН | M, кН.м | q, 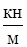
| a, м | b, м | с, м | d, м |
| 1,0 | 1,0 | 0,7 | 2,1 | 2,1 | 0,7 | |||
| 2,0 | 2,0 | 0,6 | 2,2 | 2,2 | 0,6 | |||
| 3,0 | 3,0 | 0,5 | 2,3 | 2,3 | 0,5 | |||
| 4,0 | 4,0 | 0,4 | 2,4 | 2,4 | 0,4 | |||
| 5,0 | 5,0 | 0,5 | 2,5 | 2,5 | 0,5 | |||
| 6,0 | 6,0 | 0,6 | 2,6 | 2,6 | 0,6 | |||
| 7,0 | 7,0 | 0,7 | 2,7 | 2,7 | 0,7 | |||
| 8,0 | 8,0 | 0,8 | 2,8 | 2,8 | 0,8 | |||
| 9,0 | 9,0 | 0,9 | 2,9 | 2,9 | 0,9 | |||
| 10,0 | 10,0 | 1,0 | 2,0 | 2,0 | 1,0 | |||
| в | а | б | в | а | б | в | а |
Пример 3
Задание: Построить эпюры поперечных сил Qy и изгибающего момента Mx .
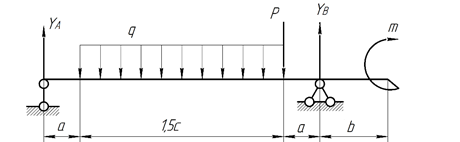
Рис.1 Заданная система
Таблица № 1. Исходные данные
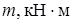
| P, кН | q, кН/м | a, м | b, м | c, м |
| 2,0 | 1,0 | 0,8 | 1,5 |
Решение
Определение опорных реакций.
Для определения реакций составляем сумму моментов всех сил относительно точек A и B. Принимаем первоначально направление реакций снизу вверх.
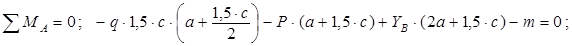
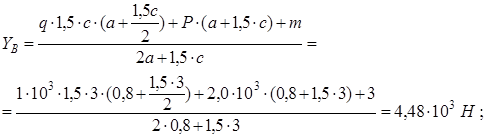
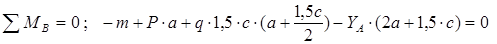
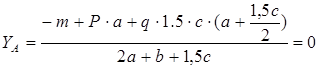
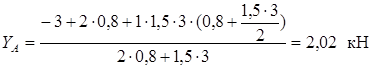
Знак плюс у реакций YA и YB показывает, что направление реакций было выбрано верно. Для проверки правильности определения опорных реакций используем условие равновесия
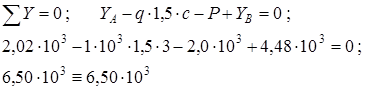
Следовательно, опорные реакции определены правильно.
Составим выражения для определения поперечной силы Qy и изгибающего моментаMx на участках балки. Балка имеет четыре силовых участка.
Первый участок 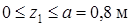 .
.
Из условия равновесия части балки, лежащей левее сечения, имеем:

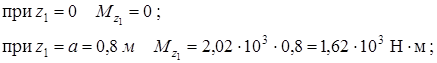
Второй участок 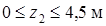 .
.
Рассматривая условия равновесия части балки, лежащей левее сечения, найдем
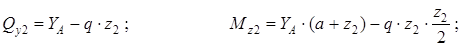
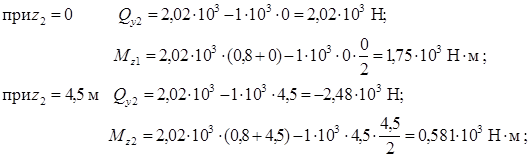
Так как в пределах участка 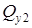 меняет знак, определим положение сечения, где
меняет знак, определим положение сечения, где 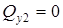 и найдем в этом сечении значение
и найдем в этом сечении значение 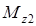 .
.
Приравняем нулю выражение поперечной силы на втором участке: 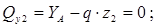 получим
получим 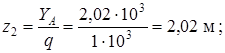
Подставив найденное значение z2 в выражение изгибающего момента 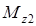 , вычислим
, вычислим 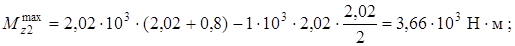
Третий участок 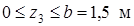 .
.
Из условия равновесия части балки, лежащей правее сечения, имеем:
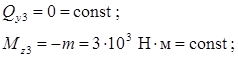
Четвертый участок 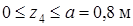 .
.
Рассматривая условия равновесия части балки, лежащей правее сечения, найдем
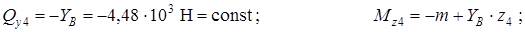
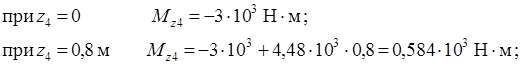
По найденным значениям Mx и Qy для всех участков построим их эпюры.
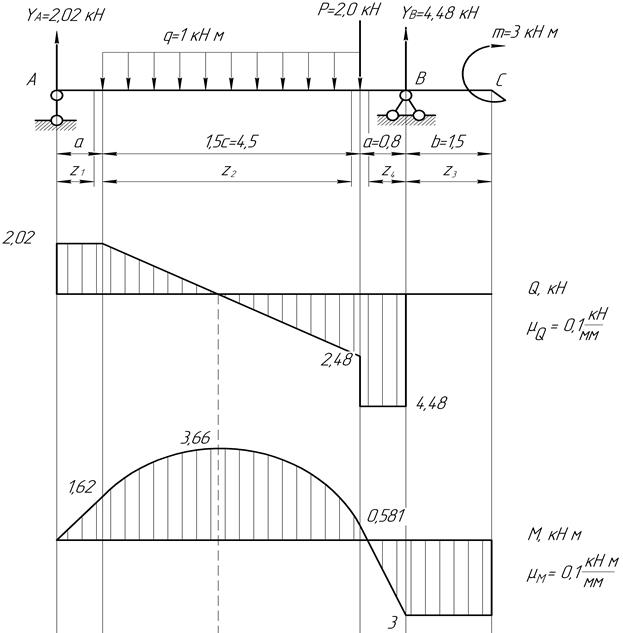
Задача 4
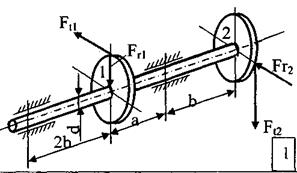
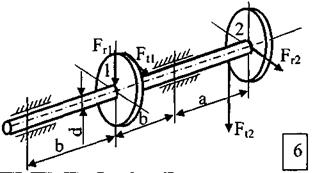
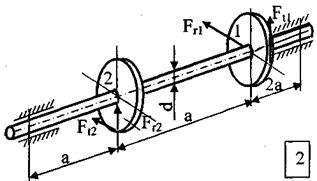
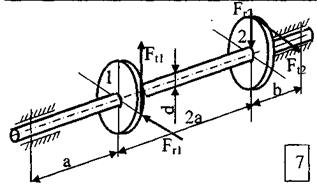
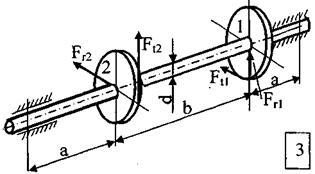
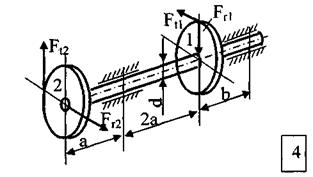
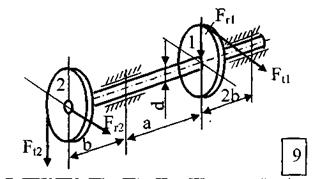
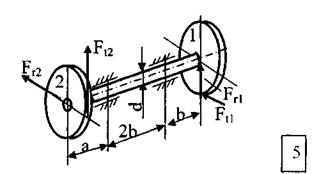
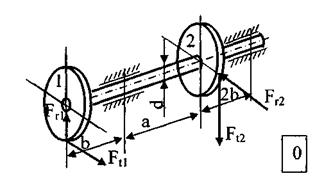
Стальной вал вращается с постоянной частотой n и передаёт мощность N.
ТРЕБУЕТСЯ:
1. Определить нагрузки, действующие на вал (радиальную силу, действующую в зацеплении принять 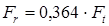 );
);
2. Построить эпюру крутящих моментов, эпюры изгибающих моментов в двух плоскостях (вертикальной и горизонтальной);
3. Подобрать диаметр вала, используя третью теорию прочности (теорию наибольших касательных напряжений) или пятую теорию прочности (энергетическую теорию прочности), если известно допускаемое напряжение 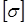 . Полученный результат округлить до ближайшего большего значения из стандартного ряда: 10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 33; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 115; 120; 125; 130 и далее через 10 мм.
. Полученный результат округлить до ближайшего большего значения из стандартного ряда: 10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 33; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 115; 120; 125; 130 и далее через 10 мм.
Исходные данные к задаче
| № строки | Схема по рис. | N, кВт | n, об/мин |
МПа | Теория прочности | а, мм | в, мм | Диаметры зубчатых колес | |||
D  ,
мм ,
мм
| D  ,
мм ,
мм
| ||||||||||
| Третья | |||||||||||
| Четвёртая | |||||||||||
| Третья | |||||||||||
| Четвёртая | |||||||||||
| Третья | |||||||||||
| Четвёртая | |||||||||||
| Третья | |||||||||||
| Четвёртая | |||||||||||
| Третья | |||||||||||
| Четвёртая | |||||||||||
| в | в | б | в | в | б | в | в | ||||
|
|
| ||||||||||
|
|
| ||||||||||
|
|
| ||||||||||
|
|
| ||||||||||
|
|
| ||||||||||
Пример
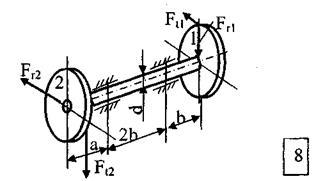
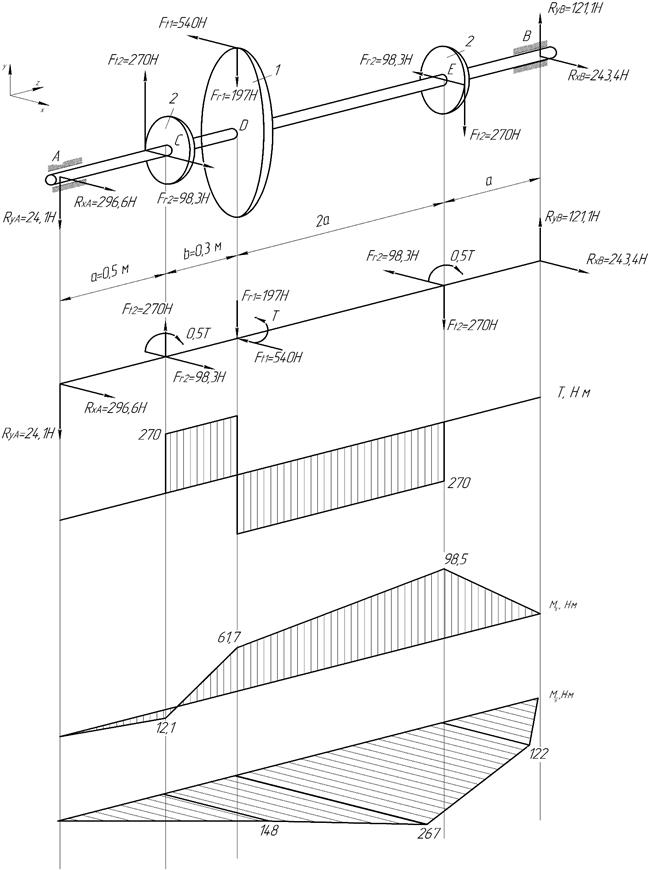
Крутящий момент Т1 от зубчатого колеса 1передаётся зубчатым колёсам 2,3.
Определить диаметр вала из условия прочности, используя критерий текучести Мизеса.
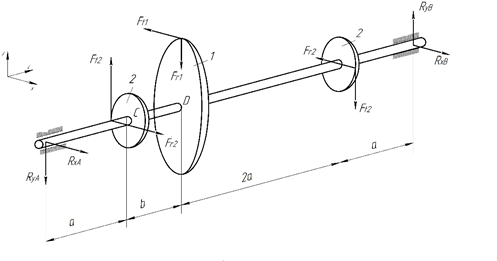
Заданная система
Таблица № 1. Исходные данные
| N, кВт | 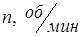
| 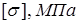
| 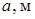
| 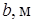
| 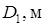
| 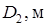
|
| 0,50 | 0,30 | 0,60 | 0,30 |
Решение
Определим величину крутящего момента, передаваемого зубчатыми колёсами и величины окружных и радиальных сил, действующее в зацеплении зубчатых колёс.
Крутящий момент
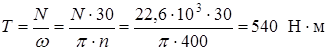 ,
,
Определяем моменты, приложенные ко вторым зубчатым колёсам.
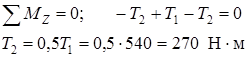 .
.
Тогда окружное усилие, действующее в зацеплении зубчатых колёс 2,
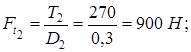
Радиальные усилия, действующие в зацеплении 1 и 2 колёс,
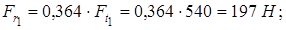
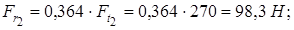
Определим реакции опор
Рассмотрим силы, действующие в вертикальной плоскости
Для определения реакций составляем сумму моментов всех сил относительно точек A и B. Принимаем первоначально направление вертикальной составляющей реакции  сверху вниз, реакции
сверху вниз, реакции  - снизу вверх.
- снизу вверх.
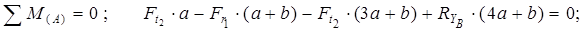
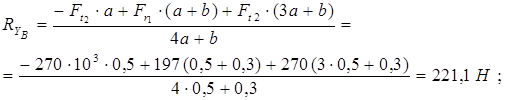
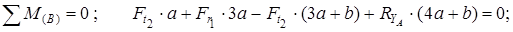
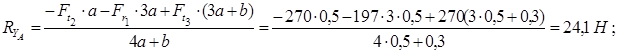
Знак плюс у реакций 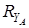 и
и 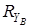 показывает, что направления реакций были выбраны верно. Для проверки правильности определения опорных реакций используем условие равновесия
показывает, что направления реакций были выбраны верно. Для проверки правильности определения опорных реакций используем условие равновесия
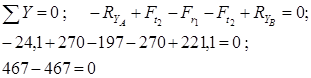
Следовательно, опорные реакции определены правильно.
Строим эпюру изгибающих моментов MX
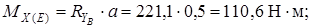
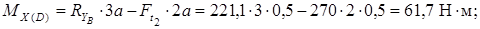
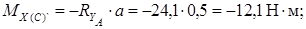
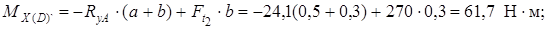
Рассмотрим силы, действующие в горизонтальной плоскости
Для определения реакций составляем сумму моментов всех сил относительно точек A и B. Принимаем первоначально направление горизонтальных составляющих реакций 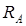 и
и 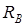 .
.
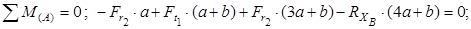
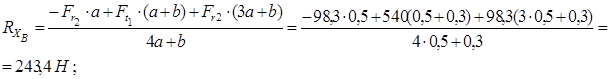
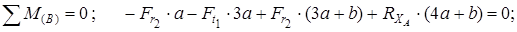
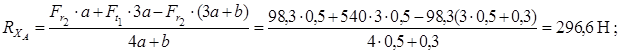 Знак плюс у реакций
Знак плюс у реакций 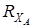 и
и 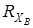 показывает, что направления реакций были выбраны верно. Для проверки правильности определения опорных реакций используем условие равновесия
показывает, что направления реакций были выбраны верно. Для проверки правильности определения опорных реакций используем условие равновесия
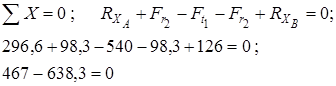
Следовательно, опорные реакции определены правильно.
Строим эпюру изгибающих моментов MY
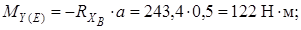
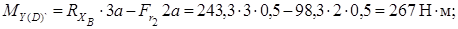
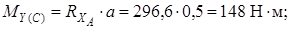
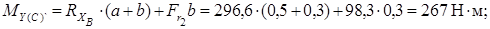
Определим опасное сечение:
Вал испытывает пространственный изгиб, то есть его изогнутая ось не лежит в одной плоскости. Устанавливаем суммарный значению изгибающий момент для каждого сечения.
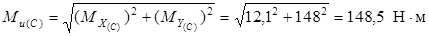
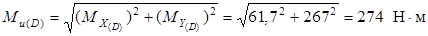
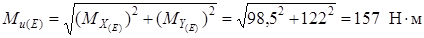
Определим диаметр вала
Опасное сечение для вала круглого поперечного сечения устанавливается по суммарному значению изгибающего момента 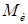 и крутящих моментов Т.
и крутящих моментов Т.
Эквивалентный (приведенный) изгибающий момент для сечения D определим по четвёртой гипотезе
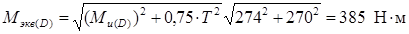 ,
,
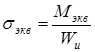 , где
, где 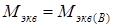 ,
, 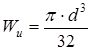 , следовательно,
, следовательно,
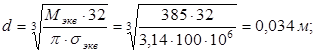
Округлим найденное значение до большего стандартного: d = 35 мм.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
 ,
,