Вывод формулы расстояния от точки до прямой.

Вывод формулы расстояния от точки до прямой.

Пусть прямая 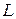на плоскости задана уравнением 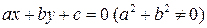. Нам нужно найти расстояние от точки 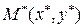до данной прямой. Опустим из точки 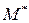перпендикуляр на прямую 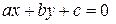. Обозначим основание перпендикуляра через 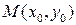. Поскольку точка 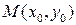лежит на нашей прямой 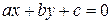, то координаты этой точки удовлетворяют уравнению прямой, то есть .

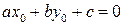Запомним это. Очевидно, что расстояние от точки 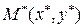до прямой 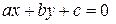равно длине отрезка 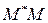. Вектор, идущий из точки 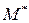в точку

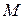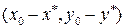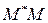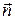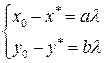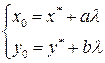, имеет координаты . Поскольку отрезок перпендикулярен нашей прямой, то он параллелен вектору нормали с координатами . Поэтому имеем следующее: или . Для 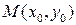, как мы помним, имеет место равенство 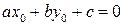. Значит, .

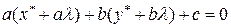Из данного соотношения найдем 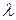. Легко видеть, что 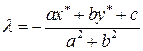. Длина отрезка 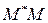с координатами 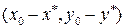равна

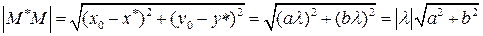Подставив в данное выражение найденное значение 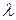, получим интересующую нас формулу расстояния от точки до прямой: .

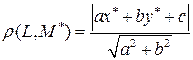Удачи в подготовке к экзаменам!