Свойства логарифмической функции и ее график

Свойства логарифмической функции и ее график

Определение

Функция вида y = log_a x, где a > 0, a ? 1, называется логарифмической функцией.

Свойства, формулы

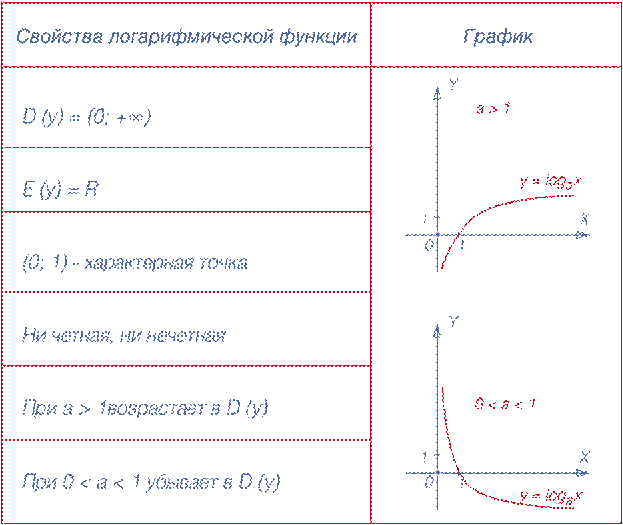
Графики

! Графики функций y = log_a x и y = log_1/a x симметричны относительно оси OX.

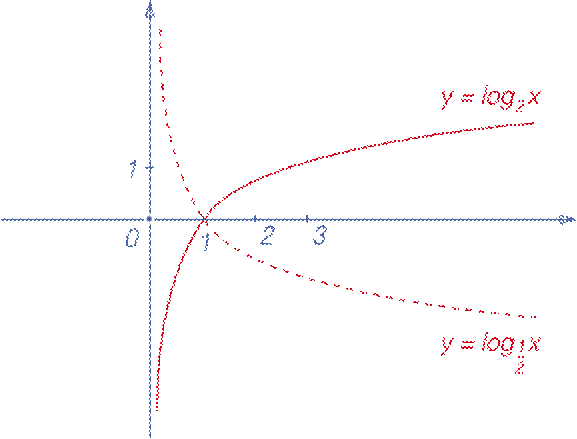
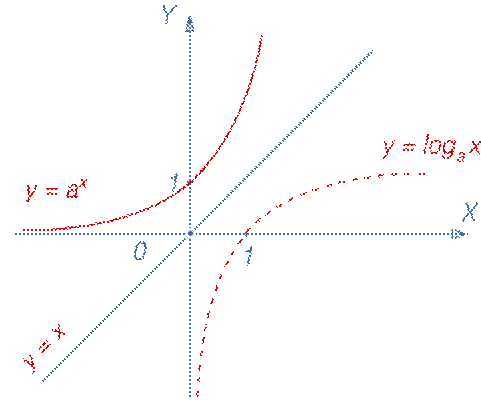
! Графики функций y = a^x и y = log_а x симметричны относительно прямой y = x.

Эти функции являются взаимно обратными.

Категория:Справочные материалыФункции и графики

Логарифмическая функция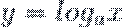

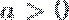
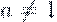
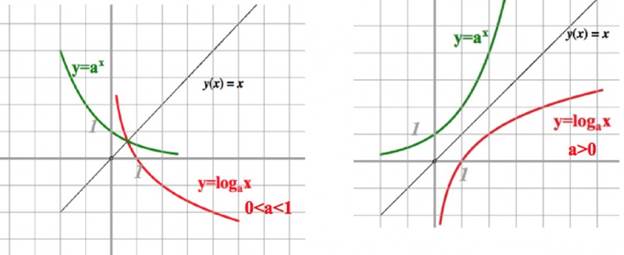
Функция (где , ) называ-

ется логарифмической функцией с основанием а.

Конечно, хорошо бы вспомнить сначала определение логарифма.

График логарифмической функции можно построить используя тот факт, что функция обратна показательной функции . Поэтому можно построить график показательной функции , после чего отобразить его симметрично относительно прямой .

И все же, как произвести построение, скажем, графика без предварительного построения графика показательной функции?

Мы должны перебирать различные значения и, подставляя в формулу, найти соответствующие значения .

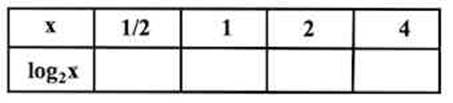
Так вот согласно определению логарифма, например, – это такая степень числа 2, в которую нужно возвести это основание 2, чтобы получить 8, то есть так как .

Руководствуясь этим правилом мы и заполняем всю таблицу (можно бы в эту таблицу дописать и такие значения , как 8, 16,…):

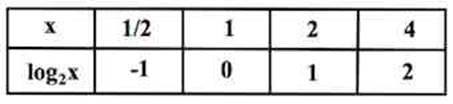
Получаем следующий график функции:

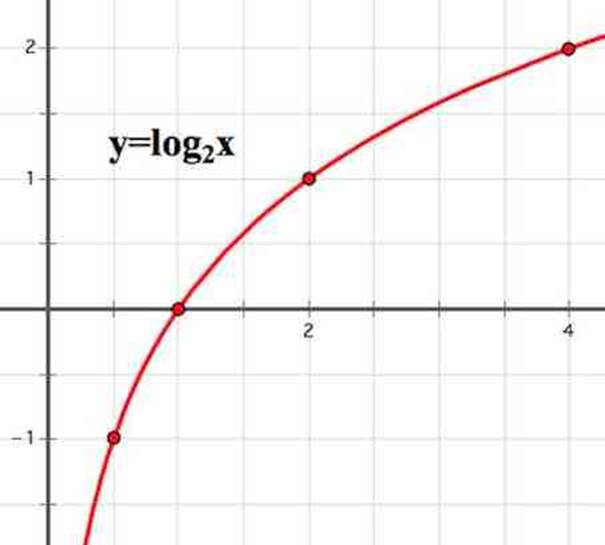
Если мы возьмем функцию , то график будет выглядеть так:

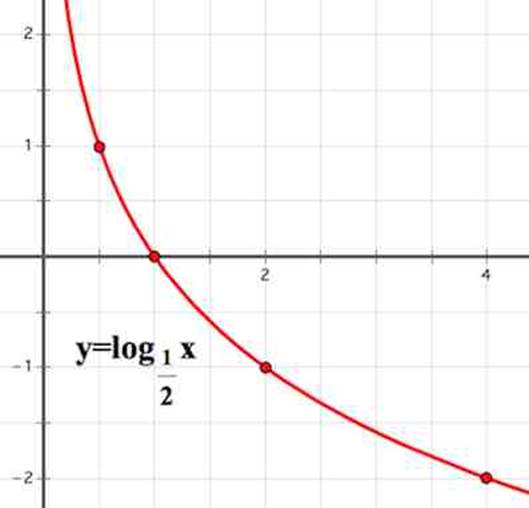
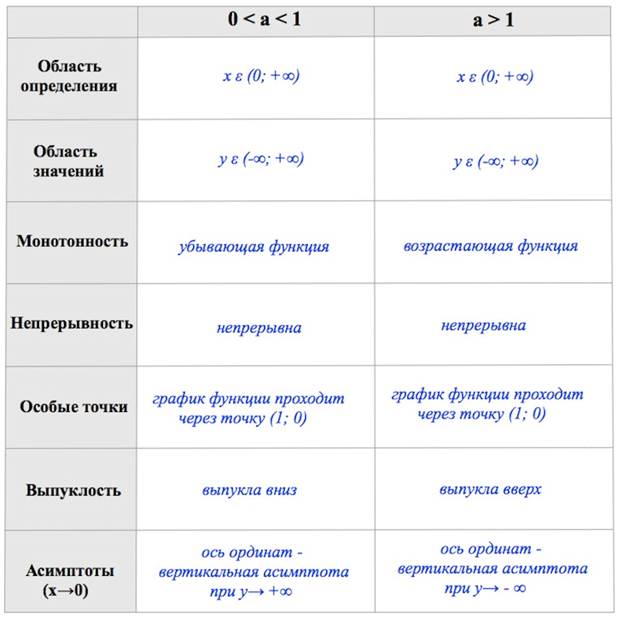
Свойства логарифмической функции

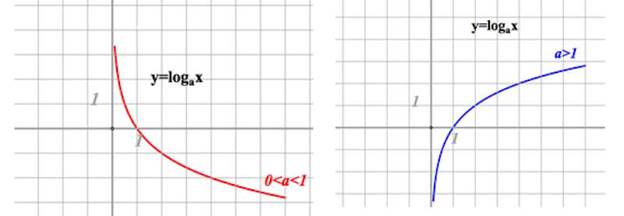
Свойства логарифмов смотрим здесь