
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Линейные отображения
Линейные отображения
L-1 L-2 R:L1 →L2 ; Отображение из L1 →L2 назыв-я линейным, если
1)Результат действия отобр-я R(aХ)=aR(X) (Однородное св-во)
2)R(x1+x2)=R(x1)+(x2) (Аддетивность)
5
Матрицей наз-ся прямоуг-я табл. Чисел к/я содержит m строк одинаковой длины(n столбцов одинак. длины) А=(аij) I-номер строки, j-номер столбца.
Матрицы=между собой если = все соответствующие элементы этих матриц,
т.е. А=В, если aij=bij. Квадратная матр.-число строк=числу столбцов. Диагональная-все элементы, кроме элементов глав-ой диагонали=0. Единичная- каждый элемент глав-ой диаг.=1. Операции:
1)Сложение матр. Только для матр. одинак. размеров. А+В=С. cij=aij+bij
2)Умножение матр. А на число к наз-ся матр. В такая, что bij=k*aij.Свойства:
1)А+В=В+А 2)А+(В+С)=(А+В)+С 3)А+0=А 4)А-А=0 5)1*А=А 6)a(А+В)=
aА+aВ 7)(a+b)А=aА+bА 8)a(bА)=(ab)А (А,В,С-матр. a,b-числа).
Ранг матр.- max кол-во линейно независимых строк и столбцов. Если матр. mxn, то ранг не превышает кол-во n столбцов и m строк. Св-ва ранга матр.:
1)При транспонировании матр. её ранг не меняется. 2)Если вычеркнуть из матр. нулевой ряд, то ранг матр. не изменится. 3)Ранг матр. не изменится при элементарных преобразованиях матр.
7
Определители. Квадратной матр. А порядка n можно сопоставить число detA называемое её определителем. Определитель матр. А также называют её детерменантом. Вычисление опред-ля 2-го порядка: 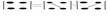
При вычисленииопределителя 3-го порядка пользуются правилом треуголь-а:
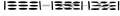
Св-ва определителей:
1)Определ-ль не изменится, если его строки заменить столбцами
2)При перестановки строк и столбцов определитель меняет знак.
3)Определитель, Имеющий 2 одинак. ряда =0.
4)Общий множитель элементов ряда можно вынести за знак определ-я.
5)Определитель не изменится если к элементам одного ряда прибавить элементы параллельного ряда умноженные на любое число.
8
Системой линейных алгебраических урав-й, содержащей m уравнений и n неизвестных, называется сис-ма вида:
 Сис-ма ур-ий наз-ся совместной если она имеет хотя бы одно решение, и несовместной если она не имеет не одного решения. Совместная сис-ма наз-ся определённой, если она имеет единственное решение, и неопределённой если она имеет более одного решения.
Сис-ма ур-ий наз-ся совместной если она имеет хотя бы одно решение, и несовместной если она не имеет не одного решения. Совместная сис-ма наз-ся определённой, если она имеет единственное решение, и неопределённой если она имеет более одного решения.
Крамер. Xi=дельтаi/дельта. Дельта=detA
Гаусс.- состоящий в последовательном исключении неизвестных. Процесс решения по методу Гаусса состоит из 2 этапов.На первом этапе сис-ма приводится к ступенчатому виду.

На втором этапе идёт последовательное определение неизвестных из этой ступенчатой сис-мы.
10
Вектор- направленный прямолинейный отрезок, он имеет опред-ю длину и опред-е направление. Коллинеарные век.- они лежат на одной прямойили на параллельных прямых. Равные век.- если они коллинеарные, одинаково направлены и имеют одинаковые длины.
Вектор ОВ соединяющий начало первого вектора с концом второго наз-ся суммой векторов a и b:ОВ=а+б.(правило треуг-ка).Правило параллелограмма:

Скалярным произведением 2ненулевых векторов а и б называется число равное произведению длин этих векторов на COS угла между ними.Св-ва:
1)(ab)=(ba)-коммутативный 2)(a1+a2)b=(a1b)+a2-аддетивность 3)(lab)=
l(ab)-однородность 4)(аа)=|a квадрат|>=0-невыроженность.
Векторнымпроизведением а и b называется вектор с длина которого = |a||b|sin угла ab. А егонаправление определяется следующим образом с^ плоск. аб (в случае когда а и б не коллинеарны ), а в случае коллиниарности с=0; где тройка векторов абс имеет положительные ориентации. Тройка абс имеет положительные ориентации <=>,когда определитель матрицы, составленный из координат этих векторов >0. Св-ва:1)антикоммутативность ab=-a(-b) 2)(a1+a2)b=(a1b)+a2-аддетивность 3)(lab)=
l(ab)-однородность 4)[aa]=0 –св-во выраженности.
Смешанное произведение векторов.Рассмотрим произведение векторов абс составленное следующим образом: (а*б)*с. Здесь первые 2 вектора перемножаются векторно, а их результат скалярно на 3 вектор.Такое произведение наз-ся смешанным произведением 3-х векторов. Произведение представляет собой некое число. Св-ва: 1) Смешанное произ-е не меняется при циклич-й перестановке его сомножителей: (ахb)*c=(bхc)*a=(cхa)*б 2)Смешанное произ-е не меняется при перемене местами знаков векторного и скалярного умножения: (ахб)*с=а*(бхс). 3)Смешанное произведение меняет свой знак при перемене мест любых 2-х векторов-сомножителей:
абс=-асб, абс=-бас, абс=-сба. 4)абс=0, то а,б,с-компланарны.
Общее уравнение прямой. Рассмотрим ур-ие первой степени относительно х и у в общем виде: Ах+Ву+С=0 (А,В,С-произвольные числа; А¹0¹В одновременно.). Частные случаи:
1)А=0 прямая || Ох 2) В=0 прямая ||Оу 3) С=0 прямая проходит через О(0,0).
Урав-е прямой с угловым коэф-м.
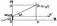 Произвольная прямая не ||Оу. aугол между прямой и Ох. a(0£a<p).М-произвольная точка прямой. Проведём через N ось Nx’ ||Ох . В системе Nх’y точка М имеет координаты х и у-b. Из определения tg угла: tga=(y-b):x; y=tga*x+b. tga=k => у=кх+б.
Нормальное уравнение прямой. Произвольная прямая не ||Оу. aугол между прямой и Ох. a(0£a<p).М-произвольная точка прямой. Проведём через N ось Nx’ ||Ох . В системе Nх’y точка М имеет координаты х и у-b. Из определения tg угла: tga=(y-b):x; y=tga*x+b. tga=k => у=кх+б.
Нормальное уравнение прямой.
 Урав-е: r*cos(j-a)-p=0; r*cosjcosa+rsinjsina-p=0.Но в силу формул связывающие прямоугольные и полярные коорд-ты имеем: rcosj=x, rsinj=y.Тогда:
x*cosa+y*sina-p=0.
Уравнение прямой проходящей через 2 точки. Пусть прямая проходит через точки
М1(х1,у1) и М2(х2,у2). Уравнение прямой проходящей через точку М1, имеет вид у-у1=к(х-х1), где к пока неизвестный коэф-т. Т.к. прямая проходит через точку М2(х2,у2), то коор-ты этой точки должны удовлетворять ур-ю: у2-у1=к(х2-х1). => к=(у2-у1):(х2-х1). Подставляем значение к в ур-ие проходящей через точки М1 и М2. Получим:
(у-у1):(у2-у1)=(х-х1):(х2-х1).
Уравнения плоскости:Ур-е плос-ти, проходящая через данную точку пенпен-но данному вектору: А(х-хо )+В(у-у0)+С(z-z0)=0. Общее ур-ие плоскости Ах+Ву+Сz+D=0. Ур-ие проходящие через 3 заданные точки: Урав-е: r*cos(j-a)-p=0; r*cosjcosa+rsinjsina-p=0.Но в силу формул связывающие прямоугольные и полярные коорд-ты имеем: rcosj=x, rsinj=y.Тогда:
x*cosa+y*sina-p=0.
Уравнение прямой проходящей через 2 точки. Пусть прямая проходит через точки
М1(х1,у1) и М2(х2,у2). Уравнение прямой проходящей через точку М1, имеет вид у-у1=к(х-х1), где к пока неизвестный коэф-т. Т.к. прямая проходит через точку М2(х2,у2), то коор-ты этой точки должны удовлетворять ур-ю: у2-у1=к(х2-х1). => к=(у2-у1):(х2-х1). Подставляем значение к в ур-ие проходящей через точки М1 и М2. Получим:
(у-у1):(у2-у1)=(х-х1):(х2-х1).
Уравнения плоскости:Ур-е плос-ти, проходящая через данную точку пенпен-но данному вектору: А(х-хо )+В(у-у0)+С(z-z0)=0. Общее ур-ие плоскости Ах+Ву+Сz+D=0. Ур-ие проходящие через 3 заданные точки:
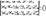 Ур-ие плос-ти в отрезках: x/a+y/b+z/c=1. Нормальное ур-ие плос-ти: Ур-ие плос-ти в отрезках: x/a+y/b+z/c=1. Нормальное ур-ие плос-ти:
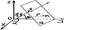 xcosa+ycosb+zcosg-p=0
Эллипсом назыв-ся множ-во всех точек плоскости, сумма расстояний от которых до двух заданных точек этой плоскости, называемых фокусами, постоянны. xcosa+ycosb+zcosg-p=0
Эллипсом назыв-ся множ-во всех точек плоскости, сумма расстояний от которых до двух заданных точек этой плоскости, называемых фокусами, постоянны.
 F1 и F2-фокусы; расстояние между ними 2с, а сумму расстояний от произвольной точки эллипса до фокусов—через 2а. По определению 2а>2с,т.е. a>c. М-произвольная точка, тогда согласно определению эллипса,
MF1+MF2=2a, т.е. Ö(х+с)квадтат+у квадр.+ Ö(х-с)квадр+у квадр.=2а
После преобразований получим (а квад—с квадр)х квадр.+а квадр.+у квадр.=а квад(а квад—с квадр). Т.к. a>c, то а квадр—с квадр>0. Получаем:
а квадр—с квадр = b квадр. Тогда последнее ур-ие примет вид: х квад/а квад +
у квадр/b квадр =1.
Гиперболой –множество точек на плоскости, разность расстояний от которых до 2х заданных точек постоянны. F1 и F2-фокусы; расстояние между ними 2с, а сумму расстояний от произвольной точки эллипса до фокусов—через 2а. По определению 2а>2с,т.е. a>c. М-произвольная точка, тогда согласно определению эллипса,
MF1+MF2=2a, т.е. Ö(х+с)квадтат+у квадр.+ Ö(х-с)квадр+у квадр.=2а
После преобразований получим (а квад—с квадр)х квадр.+а квадр.+у квадр.=а квад(а квад—с квадр). Т.к. a>c, то а квадр—с квадр>0. Получаем:
а квадр—с квадр = b квадр. Тогда последнее ур-ие примет вид: х квад/а квад +
у квадр/b квадр =1.
Гиперболой –множество точек на плоскости, разность расстояний от которых до 2х заданных точек постоянны.
 F1 и F2-фокусы; расстояние между ними 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2а. По определению 2а<2c, т.е. а<c. М—произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1-MF2|=2a т.е. Ö(х+с)квадтат+у квадр.- Ö(х-с)квадр+у квадр.=62а .После упрощений: х квад/а квад -
у квадр/b квадр =1.
Параболойназывается множ-во всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, назыв-ой директрисой. Расстояние от фокуса F до директрисы наз-ся параметром параболы и обозначается через p (p>0). F1 и F2-фокусы; расстояние между ними 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2а. По определению 2а<2c, т.е. а<c. М—произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1-MF2|=2a т.е. Ö(х+с)квадтат+у квадр.- Ö(х-с)квадр+у квадр.=62а .После упрощений: х квад/а квад -
у квадр/b квадр =1.
Параболойназывается множ-во всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, назыв-ой директрисой. Расстояние от фокуса F до директрисы наз-ся параметром параболы и обозначается через p (p>0).
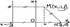 Ось Ох проходит через фокус F пенпендик-но директрисе в направлении от директрисы к F, а начало коорд-т О посередине между фокусом и директрисой. У F коор-ты (p/2; 0), а ур-ие директрисы имеет вид х=-р/2, или х+р/2=0. М—произвольная точка параболы. Соединим точку F c M. Проведём отрезок MN перпендикулярно директрисе. Из определения параболы MF=MN. По формулу между 2 точками находим: Ось Ох проходит через фокус F пенпендик-но директрисе в направлении от директрисы к F, а начало коорд-т О посередине между фокусом и директрисой. У F коор-ты (p/2; 0), а ур-ие директрисы имеет вид х=-р/2, или х+р/2=0. М—произвольная точка параболы. Соединим точку F c M. Проведём отрезок MN перпендикулярно директрисе. Из определения параболы MF=MN. По формулу между 2 точками находим:
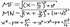 MF=MN приравняли и всё возвели в квадрат. Итого
у квадр.=2рх
Цилиндр. поверхности.Круговой цилиндр х квад.+у квад.=R квад. Параболич-й цил. х кв =2pz Гипербол-й цил. х кв/а кв. – у кв./b кв.=1 MF=MN приравняли и всё возвели в квадрат. Итого
у квадр.=2рх
Цилиндр. поверхности.Круговой цилиндр х квад.+у квад.=R квад. Параболич-й цил. х кв =2pz Гипербол-й цил. х кв/а кв. – у кв./b кв.=1
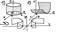 Канонические поверхности второго порядка.
Эллипсоид и Однополостный гиперболоид. Канонические поверхности второго порядка.
Эллипсоид и Однополостный гиперболоид.
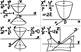
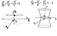 Двухполос-й гипер. Эллиптический параболоид. Гиперболический параболоид(справа снизу). Конус второго порядка. Двухполос-й гипер. Эллиптический параболоид. Гиперболический параболоид(справа снизу). Конус второго порядка.
|
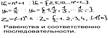 Последовательность {x} называется возрастающей, если для любого n выполняется неравенство an+1>an(an+1 /an). Анологично определяется убывающая последовательность. Un, Yn монотонные, а Zn-немонотонная. Предел последовательности:Число a называется пределом последовательности, если для любого положительного числа jнайдётся такое натуральное число N, что при всех n>N выполняется неравенство |xn–a|<j.В этом случае пишут:
Последовательность {x} называется возрастающей, если для любого n выполняется неравенство an+1>an(an+1 /an). Анологично определяется убывающая последовательность. Un, Yn монотонные, а Zn-немонотонная. Предел последовательности:Число a называется пределом последовательности, если для любого положительного числа jнайдётся такое натуральное число N, что при всех n>N выполняется неравенство |xn–a|<j.В этом случае пишут:
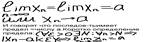 9г
22.
Функ-я на числовой прямой.
Правило по которому каждому числу из некоторого подмножества числовой прямой(наз-го областью определения) ставится в соответствии какоето вещественное число. Способы задания функ-и: 1)Аналитический f(x)=2х/(x+1) 2)табличный Элементарные функ-и: 1)f(x)=c 2)ax+b линейная функ. 3)anx^n+an-1x^n-1+an-2x^n-2… многочлены 4)х^a -степенная 5)а^x-показател-я
6)sinx, cosx-тригонометр-я 7)logax-обратная к а^x.
Свойства предела ф-ции в точке
1) Если предел в т-ке сущ-ет, то он единственный
2) Если в тке х0 предел ф-ции f(x) lim(x®x0)f(x)=A
lim(x®x0)g(x)£B=> то тогда в этой т-ке $ предел суммы, разности, произведения и частного. Отделение этих 2-х ф-ций.
а) lim(x®x0)(f(x)±g(x))=A±B
б) lim(x®x0)(f(x)*g(x))=A*B
в) lim(x®x0)(f(x):g(x))=A/B
г) lim(x®x0)C=C
д) lim(x®x0)C*f(x)=C*A
Док-во xn®x0, $ lim(x®x0)f(x)=A по опр. f(xn)®A {f(xn)}
Непрерывность функций.(в точке). Пусть функция у=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функ-я у=f(x) наз-ся непрерывной в точке х0, сли сущест-т предел функции в этой точке и он равен знач-ю функ-и в этой точке, т.е. Limf(x)=f(x0) (х-->х0). Равенство означает выполнение 3х условий: 1)Функ-я f(x) определена в точке х0 и в её окрестн-ти
2)функ-я f(x) имеет предел при х->x0. 3)предел функ-и в точке х0 равен знач-ю функ-и в этой точке, т.е. выполняется равенство. Т.к. limf(x)=f(limx)=f(x0)
(под lim х->x0). Это означает, что при нахождении придела непрерывной функции f(x) можно перейти к приделу под знаком функции, т.е. в функцию f(x) вместо аргумента х подставить его предельное значение х0.
Св-ва:1)f(x) и g(x) непрерыв. в т. х0, то их + и – также будут непрерывны. 2) функ. f(x) наз-ся непрерыв-ой на множ-ве, если она непрерывна в каждой т. этого множ-ва. 3)f(x) наз. огранич-ой сверху на множ-ве М, если сущ-т с=const такая что f(x)[c, для всех хeМ 4)f(x) наз-ся огранич-й снизу на множ-ве М, если сущ-т c=const, такая что f(x)/-с. 5)f(x) наз-ся огран-ой на множ-ве М, если сущ-т c=const: |f(x)|<c 6)с-наз-ся верх. гран. F на множ-ве М, если f(x)[c 7)c-ниж. гран. F на М, если f(x)/c. 8)Если f не огр. сверху, то supf(x)=+ ¥ 9)Если f не огр. снизу, то inff(x)= -¥
Первый замечательный предел. Lim sinx/x=1 (x->1)—это 1й замеч предел. Читается: предел отношения sin к его аргументу равен 1, когда аргумент стремится к 0.Док-во: круг R=1, радианная мера угла МОВ через х. Пусть 0<x<p/2. |AM|=sinx, дуга МВ численно равна центральному углу х, |BC|=tgх. Очевидно, имеем S^MOB<SсектораМОВ<S^COB. На основании соответствующих формул геометрии получаем 0,5sinx<0,5x<0,5tgx. Разделим неравенство на 0,5sinx>0, получим 1<x/sinx<1/cosx или cosx<sinx/x<1. Т.к.
Lim sosx=1 (x->1) и lim1=1 (x->1), тол по ризнаку (о пределе промежуточной функции) существования пределов: lim sinx/x=1 (x->1(x>0)). Пусть теперь x<0. Имеем sinx/x=sin(-x)/-x, где –х>0. Поэтому: Lim sinx/x=1 (x->0 (x<0)). =>
Наз-ся 1ое неравенство.
9г
22.
Функ-я на числовой прямой.
Правило по которому каждому числу из некоторого подмножества числовой прямой(наз-го областью определения) ставится в соответствии какоето вещественное число. Способы задания функ-и: 1)Аналитический f(x)=2х/(x+1) 2)табличный Элементарные функ-и: 1)f(x)=c 2)ax+b линейная функ. 3)anx^n+an-1x^n-1+an-2x^n-2… многочлены 4)х^a -степенная 5)а^x-показател-я
6)sinx, cosx-тригонометр-я 7)logax-обратная к а^x.
Свойства предела ф-ции в точке
1) Если предел в т-ке сущ-ет, то он единственный
2) Если в тке х0 предел ф-ции f(x) lim(x®x0)f(x)=A
lim(x®x0)g(x)£B=> то тогда в этой т-ке $ предел суммы, разности, произведения и частного. Отделение этих 2-х ф-ций.
а) lim(x®x0)(f(x)±g(x))=A±B
б) lim(x®x0)(f(x)*g(x))=A*B
в) lim(x®x0)(f(x):g(x))=A/B
г) lim(x®x0)C=C
д) lim(x®x0)C*f(x)=C*A
Док-во xn®x0, $ lim(x®x0)f(x)=A по опр. f(xn)®A {f(xn)}
Непрерывность функций.(в точке). Пусть функция у=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функ-я у=f(x) наз-ся непрерывной в точке х0, сли сущест-т предел функции в этой точке и он равен знач-ю функ-и в этой точке, т.е. Limf(x)=f(x0) (х-->х0). Равенство означает выполнение 3х условий: 1)Функ-я f(x) определена в точке х0 и в её окрестн-ти
2)функ-я f(x) имеет предел при х->x0. 3)предел функ-и в точке х0 равен знач-ю функ-и в этой точке, т.е. выполняется равенство. Т.к. limf(x)=f(limx)=f(x0)
(под lim х->x0). Это означает, что при нахождении придела непрерывной функции f(x) можно перейти к приделу под знаком функции, т.е. в функцию f(x) вместо аргумента х подставить его предельное значение х0.
Св-ва:1)f(x) и g(x) непрерыв. в т. х0, то их + и – также будут непрерывны. 2) функ. f(x) наз-ся непрерыв-ой на множ-ве, если она непрерывна в каждой т. этого множ-ва. 3)f(x) наз. огранич-ой сверху на множ-ве М, если сущ-т с=const такая что f(x)[c, для всех хeМ 4)f(x) наз-ся огранич-й снизу на множ-ве М, если сущ-т c=const, такая что f(x)/-с. 5)f(x) наз-ся огран-ой на множ-ве М, если сущ-т c=const: |f(x)|<c 6)с-наз-ся верх. гран. F на множ-ве М, если f(x)[c 7)c-ниж. гран. F на М, если f(x)/c. 8)Если f не огр. сверху, то supf(x)=+ ¥ 9)Если f не огр. снизу, то inff(x)= -¥
Первый замечательный предел. Lim sinx/x=1 (x->1)—это 1й замеч предел. Читается: предел отношения sin к его аргументу равен 1, когда аргумент стремится к 0.Док-во: круг R=1, радианная мера угла МОВ через х. Пусть 0<x<p/2. |AM|=sinx, дуга МВ численно равна центральному углу х, |BC|=tgх. Очевидно, имеем S^MOB<SсектораМОВ<S^COB. На основании соответствующих формул геометрии получаем 0,5sinx<0,5x<0,5tgx. Разделим неравенство на 0,5sinx>0, получим 1<x/sinx<1/cosx или cosx<sinx/x<1. Т.к.
Lim sosx=1 (x->1) и lim1=1 (x->1), тол по ризнаку (о пределе промежуточной функции) существования пределов: lim sinx/x=1 (x->1(x>0)). Пусть теперь x<0. Имеем sinx/x=sin(-x)/-x, где –х>0. Поэтому: Lim sinx/x=1 (x->0 (x<0)). =>
Наз-ся 1ое неравенство.
 Второй замеч. предел.
Как известно, предел числовой последоват-ти xn=(1+1/n)^n, neN, имеет предел, равный е: lim(n®¥)(1+1/n)^n=e. Док-ем, что к числу е стремится и функция xn=(1+1/x)^x при х®¥: lim(x®¥)(1+1/x)^x=e.
Док-во
1)x®+¥ n x:n=[x] => n£x<n+1 => 1/(n+1)<1/x<1/n
Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n£(1+1/n)^x£ (1+1/n)^(n+1) (4)
Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х®+¥, n®¥)
lim(n®¥)(1+1/(n+1))^n=lim(n®¥)(1+1/(n+1))^n+1 делёное на lim(n®¥)(1+1/(n+1))=е/1=e,
lim(n®¥)(1+1/n)^n+1= lim(n®¥)(1+1/n)^n* lim(n®¥)(1+1/n)=e*1=e
2) x®-¥. Сведем эту ситуацию к пред. случаю путем
подстановки –x=t, тогда: lim(x®-¥)(1+1/x)^x = lim(t®+¥)(1-1/t)^-t= lim(t®+¥)(t/(t-1))^t= lim(t®+¥)(1+1/(t-1))^t= lim(t®+¥)(1+1/t-1)^t-1*
lim(t®+¥)(1+1/t-1)^1=e*1=e
Из 1) и 2) вытекает lim(x®¥)(1+1/x)^x=e.
Наибольшее и наименьшее значение функ-и на отрезке.
Пусть f(x) диффер-ма на отр-ке [a,b]. Как найти?
1) находим f’(x) 2)Решаем ур-ие f’(x)=0 3)Вычмсляем значение самой функции f(x) в точках x1…xn и f(a), f(b) (среди этих чисел выбиранм самое малое и самое большое значение).
Бесконечно большая функция.Фун-я у=f(x) наз-ся бесконечно большой при х->х0, если для любого числа М>0 сущ-ет число d=d(М)>0, что для всех х, удовлетворяющих неравенству 0<|x-x0|<d, выполняется неравенство |f(x)|>M. Записывают Lim f(x)= : (х->х0). Пример: у=1/(х-2) есть ббф при х->2.
Если f(x) стремится к бесконечности при х->х0 и принимает лишь положительные знач-я, то пишут limf(x)=+:(х->x0), если лишь отрицательные знач-я, то limf(x)=-:(х->x0). Функ-я у=f(x), заданная на всей числовой прямой, наз-ся беск-но боль-й при х->:,если для любого числа М>0 найдётся такое число N=M(M)>0, что при всех х, удовлетвор-х неравенству |x|>N, выполняется неравенство |f(x)>M|. Напр: у=2 степ. Х, есть ббф при х->:. Бесконечно малая функ-я.Функ-я у=f(x) наз-ся бесконечно малой при х->х0, если Limf(x)=0 (x->x0). Означает: для любого числа e>0 найдётся число d>0 такое, что для всех х, удовлетворяющих неравенству 0<|x-x0|<d, выполняется неравенство |f(x)|<e. Прим: f(x)=(x-1)квад * sinкуб
1/(x-1). (показать что функ-я при х->1 яв-ся беск-но малой).
Второй замеч. предел.
Как известно, предел числовой последоват-ти xn=(1+1/n)^n, neN, имеет предел, равный е: lim(n®¥)(1+1/n)^n=e. Док-ем, что к числу е стремится и функция xn=(1+1/x)^x при х®¥: lim(x®¥)(1+1/x)^x=e.
Док-во
1)x®+¥ n x:n=[x] => n£x<n+1 => 1/(n+1)<1/x<1/n
Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n£(1+1/n)^x£ (1+1/n)^(n+1) (4)
Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х®+¥, n®¥)
lim(n®¥)(1+1/(n+1))^n=lim(n®¥)(1+1/(n+1))^n+1 делёное на lim(n®¥)(1+1/(n+1))=е/1=e,
lim(n®¥)(1+1/n)^n+1= lim(n®¥)(1+1/n)^n* lim(n®¥)(1+1/n)=e*1=e
2) x®-¥. Сведем эту ситуацию к пред. случаю путем
подстановки –x=t, тогда: lim(x®-¥)(1+1/x)^x = lim(t®+¥)(1-1/t)^-t= lim(t®+¥)(t/(t-1))^t= lim(t®+¥)(1+1/(t-1))^t= lim(t®+¥)(1+1/t-1)^t-1*
lim(t®+¥)(1+1/t-1)^1=e*1=e
Из 1) и 2) вытекает lim(x®¥)(1+1/x)^x=e.
Наибольшее и наименьшее значение функ-и на отрезке.
Пусть f(x) диффер-ма на отр-ке [a,b]. Как найти?
1) находим f’(x) 2)Решаем ур-ие f’(x)=0 3)Вычмсляем значение самой функции f(x) в точках x1…xn и f(a), f(b) (среди этих чисел выбиранм самое малое и самое большое значение).
Бесконечно большая функция.Фун-я у=f(x) наз-ся бесконечно большой при х->х0, если для любого числа М>0 сущ-ет число d=d(М)>0, что для всех х, удовлетворяющих неравенству 0<|x-x0|<d, выполняется неравенство |f(x)|>M. Записывают Lim f(x)= : (х->х0). Пример: у=1/(х-2) есть ббф при х->2.
Если f(x) стремится к бесконечности при х->х0 и принимает лишь положительные знач-я, то пишут limf(x)=+:(х->x0), если лишь отрицательные знач-я, то limf(x)=-:(х->x0). Функ-я у=f(x), заданная на всей числовой прямой, наз-ся беск-но боль-й при х->:,если для любого числа М>0 найдётся такое число N=M(M)>0, что при всех х, удовлетвор-х неравенству |x|>N, выполняется неравенство |f(x)>M|. Напр: у=2 степ. Х, есть ббф при х->:. Бесконечно малая функ-я.Функ-я у=f(x) наз-ся бесконечно малой при х->х0, если Limf(x)=0 (x->x0). Означает: для любого числа e>0 найдётся число d>0 такое, что для всех х, удовлетворяющих неравенству 0<|x-x0|<d, выполняется неравенство |f(x)|<e. Прим: f(x)=(x-1)квад * sinкуб
1/(x-1). (показать что функ-я при х->1 яв-ся беск-но малой).
 Б/м ф-ции и их сравнения
Опр. Ф-ция a(х) наз-ся б/м если ее предел в этой т-ке равен 0 из этого определения вытекает следующее св-во б/м ф-ций:
а) Алгебраическая сумма и произведение б/м ф-ций есть б/м ф-ции.
б) Произведение б/м ф-ции на ограниченную ф-цию есть б/м ф-ция, т.е. если a(х)®0 при х®х0, а f(x) определена и ограничена ($ С:½j(х)½£С)=> j(х)a(х)®0 при х®х0
Для того чтобы различать б/м по их скорости стремления к 0 вводят сл. понятие:
1) Если отношение 2-х б/м a(х)/b(х)®0 при х®х0 то говорят что б/м a имеет более высокий порядок малости чем b.
2) Если a(х)/b(х)®A¹0 при х®х0 (A-число), то a(х) и b(х) наз-ся б/м одного порядка.
3) если a(х)/b(х)®1 , то a(х) и b(х) наз-ся эквивалентными б/м (a(х)~b(х)), при х®х0.
4) Если a(х)/b^n(х)®А¹0, то a(х) наз-ся б/м n-ного порядка относительно b(х).
Аналогичные определения для случаев: х®х0-, х®х0+, х®-¥, х®+¥ и х®¥.
Производные тригонометр-х функ-й. (y=sinx, y=cosx, y=tgx, y=ctgx)
Для функ-и Y=sinx имеем:
Б/м ф-ции и их сравнения
Опр. Ф-ция a(х) наз-ся б/м если ее предел в этой т-ке равен 0 из этого определения вытекает следующее св-во б/м ф-ций:
а) Алгебраическая сумма и произведение б/м ф-ций есть б/м ф-ции.
б) Произведение б/м ф-ции на ограниченную ф-цию есть б/м ф-ция, т.е. если a(х)®0 при х®х0, а f(x) определена и ограничена ($ С:½j(х)½£С)=> j(х)a(х)®0 при х®х0
Для того чтобы различать б/м по их скорости стремления к 0 вводят сл. понятие:
1) Если отношение 2-х б/м a(х)/b(х)®0 при х®х0 то говорят что б/м a имеет более высокий порядок малости чем b.
2) Если a(х)/b(х)®A¹0 при х®х0 (A-число), то a(х) и b(х) наз-ся б/м одного порядка.
3) если a(х)/b(х)®1 , то a(х) и b(х) наз-ся эквивалентными б/м (a(х)~b(х)), при х®х0.
4) Если a(х)/b^n(х)®А¹0, то a(х) наз-ся б/м n-ного порядка относительно b(х).
Аналогичные определения для случаев: х®х0-, х®х0+, х®-¥, х®+¥ и х®¥.
Производные тригонометр-х функ-й. (y=sinx, y=cosx, y=tgx, y=ctgx)
Для функ-и Y=sinx имеем:
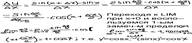 Найдём производ-ю функ-и y=cosx, воспользовавшись формулой произ-ой сложной функ-и:
Найдём производ-ю функ-и y=cosx, воспользовавшись формулой произ-ой сложной функ-и:
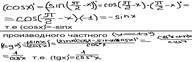 Аналогично получим Ctg.
Производные элементарных функ-й.
Аналогично получим Ctg.
Производные элементарных функ-й.
 Предел. Односторонний предел.
Число А наз-ся пределом справа (слева) функ-и f(x) в точке х0, если для всех j>0 сущ-т d>0, такое что |f(x)-A|<j, как только 0<x-x0<d. Св-ва:
1)f(x)=c, lim(x->x0)f(x)=c 2) lim(x->x0)f(x)=a, lim(x->x0)g(x)=b, lim(x->x0) f(x)+ lim(x->x0)g(x)=a+b; lim(x->x0)f(x)* lim(x->x0)g(x)=a*b
lim(x->x0)f(x) /lim(x->x0)g(x)=a/b 3)Если f(x)[c, lim(x->x0)f(x)[c
4) Если f(x)/g(x), но f(x)[c и lim(x->x0)g(x)=lim(x->x0) c(x)=A, то lim(x->x0)f(x)=A Непрерывность.Пусть f(x) определяется в окрест-ти х0, говорят, что f(x) непрерывна в точке x0, если lim(x->x0)f(x)=f(x0), т.е. для всех j>0. сущ-т d>0, что |f(x)-f(x0)|< j, как только |x-x0|<d
Пр-ные и дифференциалы выс. порядков.
Пр-ная f‘(x) – первого порядка; f‘‘(x) – второго; f‘‘‘(x)-третьего; f^n(x)=(f^(n-1)(x))‘. Пр-ные начиная со второй наз-ся пр-ными выс. порядка.
Дифференциал выс. порядков
dy= f‘(x)dx – диф. первого порядка ф-ции f(x) и обозначается d^2y, т.е. d^2y=f‘‘(x)(dx)^2. Диф. d(d^(n-1)y) от диф. d^(n-1)y наз-ся диф. n-ного порядка ф-ции f(x) и обознач. d^ny.
Т-ма Тейлора. «О приближении гладкой ф-ци к полиномам»
Опр. Пусть ф-ция f(x) имеет в т-ке а и некоторой ее окрестности пр-ные порядка n+1. Пусть х - любое значение аргумента из указанной окрестности, х¹а. Тогда между т-ми а и х надутся т-ка e такая, что справедлива ф-ла Тейлора. f(x)=f(a)+f‘(a)/1!(x+a)+ f‘‘(a)/2!(x+a)^2+f^(n)(а)/n!+f^(n+1)(e)/(n+1)!(x+a)^(n+1).
Док-во. Сводится к Роллю путем введения вспом. переменной g(x).
g(x)=f(x)-f(a)-f‘(x)(x-a)-…-1/n!*f^n(x)(x-a)^n-1/(n+1)!(x-a)^n+1*l. По т-ме Роляя $ т-ка с из (a,b), такая что g(c)=0 l=f^(n+1)(c)
33.
Т-ма Ролля
Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.
Предел. Односторонний предел.
Число А наз-ся пределом справа (слева) функ-и f(x) в точке х0, если для всех j>0 сущ-т d>0, такое что |f(x)-A|<j, как только 0<x-x0<d. Св-ва:
1)f(x)=c, lim(x->x0)f(x)=c 2) lim(x->x0)f(x)=a, lim(x->x0)g(x)=b, lim(x->x0) f(x)+ lim(x->x0)g(x)=a+b; lim(x->x0)f(x)* lim(x->x0)g(x)=a*b
lim(x->x0)f(x) /lim(x->x0)g(x)=a/b 3)Если f(x)[c, lim(x->x0)f(x)[c
4) Если f(x)/g(x), но f(x)[c и lim(x->x0)g(x)=lim(x->x0) c(x)=A, то lim(x->x0)f(x)=A Непрерывность.Пусть f(x) определяется в окрест-ти х0, говорят, что f(x) непрерывна в точке x0, если lim(x->x0)f(x)=f(x0), т.е. для всех j>0. сущ-т d>0, что |f(x)-f(x0)|< j, как только |x-x0|<d
Пр-ные и дифференциалы выс. порядков.
Пр-ная f‘(x) – первого порядка; f‘‘(x) – второго; f‘‘‘(x)-третьего; f^n(x)=(f^(n-1)(x))‘. Пр-ные начиная со второй наз-ся пр-ными выс. порядка.
Дифференциал выс. порядков
dy= f‘(x)dx – диф. первого порядка ф-ции f(x) и обозначается d^2y, т.е. d^2y=f‘‘(x)(dx)^2. Диф. d(d^(n-1)y) от диф. d^(n-1)y наз-ся диф. n-ного порядка ф-ции f(x) и обознач. d^ny.
Т-ма Тейлора. «О приближении гладкой ф-ци к полиномам»
Опр. Пусть ф-ция f(x) имеет в т-ке а и некоторой ее окрестности пр-ные порядка n+1. Пусть х - любое значение аргумента из указанной окрестности, х¹а. Тогда между т-ми а и х надутся т-ка e такая, что справедлива ф-ла Тейлора. f(x)=f(a)+f‘(a)/1!(x+a)+ f‘‘(a)/2!(x+a)^2+f^(n)(а)/n!+f^(n+1)(e)/(n+1)!(x+a)^(n+1).
Док-во. Сводится к Роллю путем введения вспом. переменной g(x).
g(x)=f(x)-f(a)-f‘(x)(x-a)-…-1/n!*f^n(x)(x-a)^n-1/(n+1)!(x-a)^n+1*l. По т-ме Роляя $ т-ка с из (a,b), такая что g(c)=0 l=f^(n+1)(c)
33.
Т-ма Ролля
Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.
 Док-во. Р-рим сначала, тривиальный случай, f(x) постоянная на [a,b] (f(a)=f(b)), тогда f‘(x)=0 $ x Î (a,b), любую т-ку можно взять в кач-ве с. Пусть f¹ const на [a,b], т.к. она непрер. на этом отрезке, то по т-ме Вейерштрасса она достигает своего экстрем. на этом отрезке и max и min. Поскольку f принимает равные знач. в гранич. т-ках, то хотя бы 1- экстр. – max или min обязательно достигается во внутр. т-ке. сÎ(a,b) (в противном случае f=const), то по т-ме Ферма, тогда f‘(c)=0, что и требовалось д-ть Т-ма Ферма. Если диф. на интервале (a,b) f(x) имеет в т-ке ч0 локальный экстремум, то пр-ная этой ф-ции обращается в 0, т.е. f‘(x0)=0 (8). Это необходимое усл. локал. экстр., но недостаточное.
Опр. Все т-ки в которых пр-ная ф-ции f(x) обращается в 0 наз-ся крит. т-ми f(x). Из т-мы Ферма => экстремум надо искать только через крит. т-ки.
34.
Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство:применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.
Док-во. Р-рим сначала, тривиальный случай, f(x) постоянная на [a,b] (f(a)=f(b)), тогда f‘(x)=0 $ x Î (a,b), любую т-ку можно взять в кач-ве с. Пусть f¹ const на [a,b], т.к. она непрер. на этом отрезке, то по т-ме Вейерштрасса она достигает своего экстрем. на этом отрезке и max и min. Поскольку f принимает равные знач. в гранич. т-ках, то хотя бы 1- экстр. – max или min обязательно достигается во внутр. т-ке. сÎ(a,b) (в противном случае f=const), то по т-ме Ферма, тогда f‘(c)=0, что и требовалось д-ть Т-ма Ферма. Если диф. на интервале (a,b) f(x) имеет в т-ке ч0 локальный экстремум, то пр-ная этой ф-ции обращается в 0, т.е. f‘(x0)=0 (8). Это необходимое усл. локал. экстр., но недостаточное.
Опр. Все т-ки в которых пр-ная ф-ции f(x) обращается в 0 наз-ся крит. т-ми f(x). Из т-мы Ферма => экстремум надо искать только через крит. т-ки.
34.
Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство:применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.
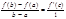
 Теорема: пусть f диффер-ма на интервале (a,b) и f невозр-т на (a,b) ¢5$ когда f’[0 на (a,b). Достат-ть: х1:х2e(a,b) 0/f(x2)-f(x1)=f’(c)(x2-x1), ce(x1,x2), x2>x1, f(x2)[f(x1) Необход-ть: f’(x0)=lim(x->x0)f(x)-f(x0)/(x-x0)
1)x<x0 x-x0<0 f(x)/f(x0) 2)x>x0 x-x0>0 f(x)[f(x0)
Т-ма. Пусть f(x) диффер. На интервале (a,b), тогда справедливы сл. утверждения f(x) монотонно возр. (убывает) на интервале (a,b) тогда, когда f‘(x)³0 на интервале (a,b) и f‘(x)>0 (f‘(x)<0), то строго возр. (убыв) на (a,b).
хÎ интерв. монотонно убывает, касательная имеет тупой угол наклона f‘(x1)<0 для x2 противоположная ситуация.
Теорема: пусть f диффер-ма на интервале (a,b) и f невозр-т на (a,b) ¢5$ когда f’[0 на (a,b). Достат-ть: х1:х2e(a,b) 0/f(x2)-f(x1)=f’(c)(x2-x1), ce(x1,x2), x2>x1, f(x2)[f(x1) Необход-ть: f’(x0)=lim(x->x0)f(x)-f(x0)/(x-x0)
1)x<x0 x-x0<0 f(x)/f(x0) 2)x>x0 x-x0>0 f(x)[f(x0)
Т-ма. Пусть f(x) диффер. На интервале (a,b), тогда справедливы сл. утверждения f(x) монотонно возр. (убывает) на интервале (a,b) тогда, когда f‘(x)³0 на интервале (a,b) и f‘(x)>0 (f‘(x)<0), то строго возр. (убыв) на (a,b).
хÎ интерв. монотонно убывает, касательная имеет тупой угол наклона f‘(x1)<0 для x2 противоположная ситуация.
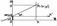 Произвольная прямая не ||Оу. aугол между прямой и Ох. a(0£a<p).М-произвольная точка прямой. Проведём через N ось Nx’ ||Ох . В системе Nх’y точка М имеет координаты х и у-b. Из определения tg угла: tga=(y-b):x; y=tga*x+b. tga=k => у=кх+б.
Нормальное уравнение прямой.
Произвольная прямая не ||Оу. aугол между прямой и Ох. a(0£a<p).М-произвольная точка прямой. Проведём через N ось Nx’ ||Ох . В системе Nх’y точка М имеет координаты х и у-b. Из определения tg угла: tga=(y-b):x; y=tga*x+b. tga=k => у=кх+б.
Нормальное уравнение прямой.
 Урав-е: r*cos(j-a)-p=0; r*cosjcosa+rsinjsina-p=0.Но в силу формул связывающие прямоугольные и полярные коорд-ты имеем: rcosj=x, rsinj=y.Тогда:
x*cosa+y*sina-p=0.
Уравнение прямой проходящей через 2 точки. Пусть прямая проходит через точки
М1(х1,у1) и М2(х2,у2). Уравнение прямой проходящей через точку М1, имеет вид у-у1=к(х-х1), где к пока неизвестный коэф-т. Т.к. прямая проходит через точку М2(х2,у2), то коор-ты этой точки должны удовлетворять ур-ю: у2-у1=к(х2-х1). => к=(у2-у1):(х2-х1). Подставляем значение к в ур-ие проходящей через точки М1 и М2. Получим:
(у-у1):(у2-у1)=(х-х1):(х2-х1).
Уравнения плоскости:Ур-е плос-ти, проходящая через данную точку пенпен-но данному вектору: А(х-хо )+В(у-у0)+С(z-z0)=0. Общее ур-ие плоскости Ах+Ву+Сz+D=0. Ур-ие проходящие через 3 заданные точки:
Урав-е: r*cos(j-a)-p=0; r*cosjcosa+rsinjsina-p=0.Но в силу формул связывающие прямоугольные и полярные коорд-ты имеем: rcosj=x, rsinj=y.Тогда:
x*cosa+y*sina-p=0.
Уравнение прямой проходящей через 2 точки. Пусть прямая проходит через точки
М1(х1,у1) и М2(х2,у2). Уравнение прямой проходящей через точку М1, имеет вид у-у1=к(х-х1), где к пока неизвестный коэф-т. Т.к. прямая проходит через точку М2(х2,у2), то коор-ты этой точки должны удовлетворять ур-ю: у2-у1=к(х2-х1). => к=(у2-у1):(х2-х1). Подставляем значение к в ур-ие проходящей через точки М1 и М2. Получим:
(у-у1):(у2-у1)=(х-х1):(х2-х1).
Уравнения плоскости:Ур-е плос-ти, проходящая через данную точку пенпен-но данному вектору: А(х-хо )+В(у-у0)+С(z-z0)=0. Общее ур-ие плоскости Ах+Ву+Сz+D=0. Ур-ие проходящие через 3 заданные точки:
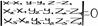 Ур-ие плос-ти в отрезках: x/a+y/b+z/c=1. Нормальное ур-ие плос-ти:
Ур-ие плос-ти в отрезках: x/a+y/b+z/c=1. Нормальное ур-ие плос-ти: 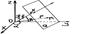 xcosa+ycosb+zcosg-p=0
Эллипсом назыв-ся множ-во всех точек плоскости, сумма расстояний от которых до двух заданных точек этой плоскости, называемых фокусами, постоянны.
xcosa+ycosb+zcosg-p=0
Эллипсом назыв-ся множ-во всех точек плоскости, сумма расстояний от которых до двух заданных точек этой плоскости, называемых фокусами, постоянны.
 F1 и F2-фокусы; расстояние между ними 2с, а сумму расстояний от произвольной точки эллипса до фокусов—через 2а. По определению 2а>2с,т.е. a>c. М-произвольная точка, тогда согласно определению эллипса,
MF1+MF2=2a, т.е. Ö(х+с)квадтат+у квадр.+ Ö(х-с)квадр+у квадр.=2а
После преобразований получим (а квад—с квадр)х квадр.+а квадр.+у квадр.=а квад(а квад—с квадр). Т.к. a>c, то а квадр—с квадр>0. Получаем:
а квадр—с квадр = b квадр. Тогда последнее ур-ие примет вид: х квад/а квад +
у квадр/b квадр =1.
Гиперболой –множество точек на плоскости, разность расстояний от которых до 2х заданных точек постоянны.
F1 и F2-фокусы; расстояние между ними 2с, а сумму расстояний от произвольной точки эллипса до фокусов—через 2а. По определению 2а>2с,т.е. a>c. М-произвольная точка, тогда согласно определению эллипса,
MF1+MF2=2a, т.е. Ö(х+с)квадтат+у квадр.+ Ö(х-с)квадр+у квадр.=2а
После преобразований получим (а квад—с квадр)х квадр.+а квадр.+у квадр.=а квад(а квад—с квадр). Т.к. a>c, то а квадр—с квадр>0. Получаем:
а квадр—с квадр = b квадр. Тогда последнее ур-ие примет вид: х квад/а квад +
у квадр/b квадр =1.
Гиперболой –множество точек на плоскости, разность расстояний от которых до 2х заданных точек постоянны.
 F1 и F2-фокусы; расстояние между ними 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2а. По определению 2а<2c, т.е. а<c. М—произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1-MF2|=2a т.е. Ö(х+с)квадтат+у квадр.- Ö(х-с)квадр+у квадр.=62а .После упрощений: х квад/а квад -
у квадр/b квадр =1.
Параболойназывается множ-во всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, назыв-ой директрисой. Расстояние от фокуса F до директрисы наз-ся параметром параболы и обозначается через p (p>0).
F1 и F2-фокусы; расстояние между ними 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2а. По определению 2а<2c, т.е. а<c. М—произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1-MF2|=2a т.е. Ö(х+с)квадтат+у квадр.- Ö(х-с)квадр+у квадр.=62а .После упрощений: х квад/а квад -
у квадр/b квадр =1.
Параболойназывается множ-во всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, назыв-ой директрисой. Расстояние от фокуса F до директрисы наз-ся параметром параболы и обозначается через p (p>0).
 Ось Ох проходит через фокус F пенпендик-но директрисе в направлении от директрисы к F, а начало коорд-т О посередине между фокусом и директрисой. У F коор-ты (p/2; 0), а ур-ие директрисы имеет вид х=-р/2, или х+р/2=0. М—произвольная точка параболы. Соединим точку F c M. Проведём отрезок MN перпендикулярно директрисе. Из определения параболы MF=MN. По формулу между 2 точками находим:
Ось Ох проходит через фокус F пенпендик-но директрисе в направлении от директрисы к F, а начало коорд-т О посередине между фокусом и директрисой. У F коор-ты (p/2; 0), а ур-ие директрисы имеет вид х=-р/2, или х+р/2=0. М—произвольная точка параболы. Соединим точку F c M. Проведём отрезок MN перпендикулярно директрисе. Из определения параболы MF=MN. По формулу между 2 точками находим:
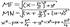 MF=MN приравняли и всё возвели в квадрат. Итого
у квадр.=2рх
Цилиндр. поверхности.Круговой цилиндр х квад.+у квад.=R квад. Параболич-й цил. х кв =2pz Гипербол-й цил. х кв/а кв. – у кв./b кв.=1
MF=MN приравняли и всё возвели в квадрат. Итого
у квадр.=2рх
Цилиндр. поверхности.Круговой цилиндр х квад.+у квад.=R квад. Параболич-й цил. х кв =2pz Гипербол-й цил. х кв/а кв. – у кв./b кв.=1
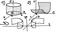 Канонические поверхности второго порядка.
Эллипсоид и Однополостный гиперболоид.
Канонические поверхности второго порядка.
Эллипсоид и Однополостный гиперболоид.
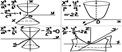
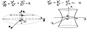 Двухполос-й гипер. Эллиптический параболоид. Гиперболический параболоид(справа снизу). Конус второго порядка.
Двухполос-й гипер. Эллиптический параболоид. Гиперболический параболоид(справа снизу). Конус второго порядка.
 Св-ва произ-х.
1)(f’6g’)=f’6g’ 2)(fg)’=f’g+fg’(фор-ла Лейбница).
Св-ва произ-х.
1)(f’6g’)=f’6g’ 2)(fg)’=f’g+fg’(фор-ла Лейбница).
 3)Произ-е частного (f/g)’=(f’g-g’f)/g^2 4)(x^n)'=(x*x^n-1)'=nx^n-1 5)f'(x)=(a0+a1x+a2x^2 +anx^n)’=nanx^n-1 6)(x^-n)’=(1/xn)’=-nx^-n-1
Геометрич-й смысл прпоиз-ой.Угловой коэф-т касательной k=tga=
=lim(дельтах->0)дельтау/дельтах. Это равенство перепишем в виде f’(x)=tga=k т.е. произ-ая f’(x) в точке х равна угловому коэф-ту касательной к графику у=f(x) в точке, абсцисса которой равна х.
Геометр-й смысл диффер-ла функ-й.Проведём к графику функ-и у=f(x) в точке М(х;у) касательную МТ ирассмотрим ординату этой касательную для точки х+дельта х. На рис. |AM|=дельта х, |AM1|=дельта у. Из прямоуг-го треуг-ка МАВ имеем: tga=|AB|/Дельтах, т.е. |AB|=tga*дельтах. Но согласно геометр-му смыслу произ-ой tga=f’(x). Поэтому АВ=f’(x)*дельта х. Сравниваем полученный результат сформулой dy=f’(x)*дельта х. (Дифферен-л функ-и у=f(x) в точке х), получаем dy=AB, т.е. дифферин-л функ-и у=f(x) в точке х равен приращению ординаты касательной к графику функ-и в этой точке, когда х получит приращение дельтах.
3)Произ-е частного (f/g)’=(f’g-g’f)/g^2 4)(x^n)'=(x*x^n-1)'=nx^n-1 5)f'(x)=(a0+a1x+a2x^2 +anx^n)’=nanx^n-1 6)(x^-n)’=(1/xn)’=-nx^-n-1
Геометрич-й смысл прпоиз-ой.Угловой коэф-т касательной k=tga=
=lim(дельтах->0)дельтау/дельтах. Это равенство перепишем в виде f’(x)=tga=k т.е. произ-ая f’(x) в точке х равна угловому коэф-ту касательной к графику у=f(x) в точке, абсцисса которой равна х.
Геометр-й смысл диффер-ла функ-й.Проведём к графику функ-и у=f(x) в точке М(х;у) касательную МТ ирассмотрим ординату этой касательную для точки х+дельта х. На рис. |AM|=дельта х, |AM1|=дельта у. Из прямоуг-го треуг-ка МАВ имеем: tga=|AB|/Дельтах, т.е. |AB|=tga*дельтах. Но согласно геометр-му смыслу произ-ой tga=f’(x). Поэтому АВ=f’(x)*дельта х. Сравниваем полученный результат сформулой dy=f’(x)*дельта х. (Дифферен-л функ-и у=f(x) в точке х), получаем dy=AB, т.е. дифферин-л функ-и у=f(x) в точке х равен приращению ординаты касательной к графику функ-и в этой точке, когда х получит приращение дельтах.
 Первообразная.Функ-я F9x) наз-ся первоб-ой для функ-и f(x), если она фиффер-ма, в каждой точке области определения и производная F=f.
(F+f)’=f. Если F первоб-ая функ-и f(x), то и все виды функ-и F+c тоже будут первооб-ми. Обратная. Пусть у f есть ещё одна первоб-ая G. G’=f. По следствию из теоремы Лангранжа: если 2 функ-и имеют одинак-ю произ-ю, то они отличаются на константу.
Множ-во всех первоб-х функ-й F(x) + C для f(x) наз-ся неопред-ым интегралом по функ-и f(x) и обознач-ся символом ∫f(x)dx. Таким образом, по опред-ю: ∫f(x)dx=F(x)+C. Здесь f(x) наз-ся подынтегральной функ-ей, f(x)dx-подынтегральным выражением, х-переменной интегрирования, ∫ - знаком неопред-го интеграла.
Св-ва: 1) ∫dF=F+C d(F+C)=(F+C)’dx=F’dx+fdx 2)d(∫fdx)=fdx 3) ∫cfdx=c∫fdx F’=f (cF)’=cf ∫cfdx={cF+b} c(∫fdx)={c(F+a)}={c F+ca} ca=b c¹0 4)Для разности можно вывести ∫(f6g)dx=∫fdx6∫gdx F’=f G’=g (F+G)’=F’+G’=(f+g)
Табличные интегралы.
Первообразная.Функ-я F9x) наз-ся первоб-ой для функ-и f(x), если она фиффер-ма, в каждой точке области определения и производная F=f.
(F+f)’=f. Если F первоб-ая функ-и f(x), то и все виды функ-и F+c тоже будут первооб-ми. Обратная. Пусть у f есть ещё одна первоб-ая G. G’=f. По следствию из теоремы Лангранжа: если 2 функ-и имеют одинак-ю произ-ю, то они отличаются на константу.
Множ-во всех первоб-х функ-й F(x) + C для f(x) наз-ся неопред-ым интегралом по функ-и f(x) и обознач-ся символом ∫f(x)dx. Таким образом, по опред-ю: ∫f(x)dx=F(x)+C. Здесь f(x) наз-ся подынтегральной функ-ей, f(x)dx-подынтегральным выражением, х-переменной интегрирования, ∫ - знаком неопред-го интеграла.
Св-ва: 1) ∫dF=F+C d(F+C)=(F+C)’dx=F’dx+fdx 2)d(∫fdx)=fdx 3) ∫cfdx=c∫fdx F’=f (cF)’=cf ∫cfdx={cF+b} c(∫fdx)={c(F+a)}={c F+ca} ca=b c¹0 4)Для разности можно вывести ∫(f6g)dx=∫fdx6∫gdx F’=f G’=g (F+G)’=F’+G’=(f+g)
Табличные интегралы.
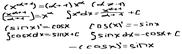
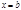 называется вертикальной асимптотой графика ф-ии
называется вертикальной асимптотой графика ф-ии 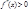 в точке b , если хотя бы один из разносторонних пределов равен бесконечности.
Если ф-ия задана дробно-рациональным выражением, то вертикальная асимптота появляется в тех точках, когда знаменатель равен нулю, а числитель не равен нулю.
********************
Наклонная асимптота – прямая
в точке b , если хотя бы один из разносторонних пределов равен бесконечности.
Если ф-ия задана дробно-рациональным выражением, то вертикальная асимптота появляется в тех точках, когда знаменатель равен нулю, а числитель не равен нулю.
********************
Наклонная асимптота – прямая 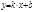 наклонная асимптота ф-ии
наклонная асимптота ф-ии 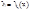 , если эта ф-ия представлена в виде
, если эта ф-ия представлена в виде 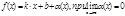 Необходимый и достаточный признак существования наклонной асимптоты:
Для существования наклонной асимптоты
Необходимый и достаточный признак существования наклонной асимптоты:
Для существования наклонной асимптоты 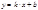 к графику ф-ии
к графику ф-ии 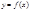 необходимо и достаточно существование конечных пределов:
необходимо и достаточно существование конечных пределов:
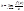
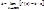 Горизонтальная асимптота-y= lim(x-») (y-kx)
41.
1)Область определения
2)Найти точки пересечения графика с осями координат
3)Найти интервалы знака постоянства(промежутки на которых f(x)>0 или f(x)<0.
4)Четность нечетность
5)Найти асимптоты
6)Найти интервалы монотонности ф-ции
7)Найти экстремумы ф-ции
8)Найти интервалы выпуклости и точки перегиба графика ф-ции.
На основании последнего исследования построить график.
46.
Дифференцирование ф-ций
Функция f(x,y) наз-ся дифер-ой в точ-ах (x0,y0), если имеет место такое неравенство f(x,y)=f(x0,y0)+a(x-x0)+b(y-y0)+φ(x,y).
Горизонтальная асимптота-y= lim(x-») (y-kx)
41.
1)Область определения
2)Найти точки пересечения графика с осями координат
3)Найти интервалы знака постоянства(промежутки на которых f(x)>0 или f(x)<0.
4)Четность нечетность
5)Найти асимптоты
6)Найти интервалы монотонности ф-ции
7)Найти экстремумы ф-ции
8)Найти интервалы выпуклости и точки перегиба графика ф-ции.
На основании последнего исследования построить график.
46.
Дифференцирование ф-ций
Функция f(x,y) наз-ся дифер-ой в точ-ах (x0,y0), если имеет место такое неравенство f(x,y)=f(x0,y0)+a(x-x0)+b(y-y0)+φ(x,y).
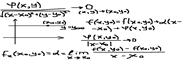 Утверждение:если функ-я f(x,y) диффер-ма в точке (x0,y0), то она непрерывна по совокупности.
Частные производные высшего порядка.
Пусть задана функция 2х переменных z=f(x,y),найдем ее частные производные.
¶z/¶x=f¢x(x,y)
¶z/¶y=f¢y(x,y)
В общем случае, эти производные также являются функциями 2х и можно искать их частные производные. При этом получаем часные производные 2-ого и более порядков.Производные, в которых дифференцирование производится по разным переменным, называются смешанными.
Теорема: О независимости часных производных от порядка (последовательности) дифференцирования.
Две смешанные частные роизводные одного порядка, отличающиеся только порядком диф-я равны.
¶2z/¶x¶y=¶2z/¶y¶x - в следствии этого, при обозначении смешанных частных производных последовательность диф-я не указывается.
¶nz/¶xn-2¶y2
47.
Z=f(x,y), M0(x0,y0), M(x,y)
Max ф-ции Z называется такое ее значение f(x0,y0), которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки M0
Min ф-ции Z называется такое ее значение f(x0,y0), которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки M0
Экстремум сущ. в тех точках, в которых частная производная ф-ции Z=0 или не существует:
Утверждение:если функ-я f(x,y) диффер-ма в точке (x0,y0), то она непрерывна по совокупности.
Частные производные высшего порядка.
Пусть задана функция 2х переменных z=f(x,y),найдем ее частные производные.
¶z/¶x=f¢x(x,y)
¶z/¶y=f¢y(x,y)
В общем случае, эти производные также являются функциями 2х и можно искать их частные производные. При этом получаем часные производные 2-ого и более порядков.Производные, в которых дифференцирование производится по разным переменным, называются смешанными.
Теорема: О независимости часных производных от порядка (последовательности) дифференцирования.
Две смешанные частные роизводные одного порядка, отличающиеся только порядком диф-я равны.
¶2z/¶x¶y=¶2z/¶y¶x - в следствии этого, при обозначении смешанных частных производных последовательность диф-я не указывается.
¶nz/¶xn-2¶y2
47.
Z=f(x,y), M0(x0,y0), M(x,y)
Max ф-ции Z называется такое ее значение f(x0,y0), которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки M0
Min ф-ции Z называется такое ее значение f(x0,y0), которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки M0
Экстремум сущ. в тех точках, в которых частная производная ф-ции Z=0 или не существует:
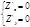 Если Z=f(x1,x2,...xn), то ¶Z/¶xi=0, i=1,2,...n - необходимое условие.
Достаточный признак:
Если Z=f(x1,x2,...xn), то ¶Z/¶xi=0, i=1,2,...n - необходимое условие.
Достаточный признак:
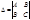 где A= Z``XX(x0,y0), C= Z``yy(x0,y0), B= Z``yx (x0,y0),
1) если D>0, то М0 - точка экстремума;
если А<0 или С<0, то М0 - точка max;
если А>0 или С>0, то М0 - точка min.
2) если D<0, то экстремума нет
3) если D=0, то вопрос о существовании экстремума остается открытым.
где A= Z``XX(x0,y0), C= Z``yy(x0,y0), B= Z``yx (x0,y0),
1) если D>0, то М0 - точка экстремума;
если А<0 или С<0, то М0 - точка max;
если А>0 или С>0, то М0 - точка min.
2) если D<0, то экстремума нет
3) если D=0, то вопрос о существовании экстремума остается открытым.