Симметрия в природе

2. Симметрия в природе

В мире растений в ходу симметрия — поворотная. Возьмите в руку цветок ромашки. Совмещение разных частей цветка происходит, если их повернуть вокруг стебелька. Здесь напрашивается короткое отступление. Очень часто флора и фауна одалживают внешние формы друг у друга. Морские звезды, ведущие растительный образ жизни, обладают поворотной симметрией, а листья — зеркальной. Как же выбирается вид симметрии? Прикованные к постоянному месту растения четко различают только верх и низ, а все остальные направления для них более или менее одинаковы. Естественно, что их внешний вид подчинен поворотной симметрии. Для животных очень важно, что находится впереди и что сзади, только «лево» и «право» для них остаются . равноправными. В этом случае господствует зеркальная симметрия. Любопытно, что животные, меняющие подвижную жизнь на неподвижную и потом вновь возвращающиеся к подвижной жизни, соответственное число раз переходят от одного вида симметрии к другому, как это случилось, например, с иглокожими (морскими звездами и др.).

Законам симметрии подчиняются все формы на свете. Даже «вечно свободные» облака обладают симметрией, хотя и искаженной. Замирая на голубом небе, они напоминают медленно движущихся в морской воде медуз, явно тяготея к поворотной симметрии, а потом, гонимые поднявшимся ветерком, меняют симметрию на зеркальную.

Замечательный немецкий математик Германа Вейль, всю жизнь интересовавшегося проблемами симметрии и посвятившего ей свой последний труд писал следующее, симметричным называется такой предмет, с которым можно проделать какую-то операцию, получив в итоге первоначальное состояние. В случае зеркальной симметрии меняются правая и левая части предмета, а при поворотной симметрии переставляются его дольки.

Если трактовать это определение достаточно широко, то эпитет «симметричный» можно распространить на весьма широкий круг понятий. Дотошные физики сделали это одними из первых, заговорив о симметрии физических законов.

Природа, точнее ее законы, обладает одним из видов симметрии — однородностью пространства: все точки пространства равноправны.

Но в пространстве взаимозаменяемы не только отдельные точки, но и коллективы точек — целые направления. Другими словами, если бы вдруг вся вселенная со всеми неисчислимыми звездными мирами плавно повернулась бы на какой-то угол, законы природы ни на йоту не изменились бы. Такое равноправие направлений, или, как говорят ученые, изотропность пространства, тоже вид симметрии. Законы природы симметричны не только относительно пространства, но и относительно времени. В самом деле, теоремы, доказанные в Древнем Египте, до сих пор изучаются школьниками. Наука уточняет старые законы, четко определяет сферу их действия, но не опровергает их, если, конечно, они не были ошибочными.

Итак, мы живем в довольно симметричном мире. Не удивительно, что сами мы симметричны и склонны считать красивым все симметричное. Иногда, правда, приятно слегка нарушить идеальную симметрию, это придает некоторую живость, но не слишком, не до хаоса. Весьма симметричны животные, довольно симметричны растения, совсем симметричны кристаллы, почти идеально симметрична наша шарообразная планета, близка к симметрии ее траектория. После сказанного, может быть, покажется не столь уж фантастичным утверждение, что все законы природы определяются симметрией мира.

Анекдотический буриданов осел погиб от голода между двумя охапками сена. Он не знал, с какой начать, так как они были совершенно одинаковы. Поведение осла кажется на первый взгляд совершенно неестественным. Однако это не так. Что может быть естественней самой природы? А она ведет себя в подобных ситуациях точь-в-точь как буриданов осел. В самом деле, если шарик неподвижен на столе, значит стол ровный и слева наклон тот же самый, что и справа. Если ток не идет по проводу, значит нет разности потенциалов. Если тучка застыла на небе, значит давление вокруг одинаково и стих ветер. Было бы странным, если бы все происходило наоборот. Природа никогда не отдает предпочтения при равенстве.

Симметрия — это и есть равенство в широком смысле этого слова. Например, зеркальная симметрия означает, что правая часть в точности равна левой. Поэтому, подобно ослу Буридана, явление, обладающее зеркальной симметрией, должно «уклоняться» от поступков, отдающих предпочтение одной из частей, сохраняя нейтральное положение. Значит, если имеет место симметрия, то чего-то не произойдет и, значит, что-то обязательно останется неизменным, сохранится.

1.1. Симметрия в зоологии

Некоторые животные, в частности большинство губок и амебоидные протозоа, лишены симметрии, имеют или нерегулярную форму, различную у разных особей, или вообще не имеют определенной формы. Однако большинство животных представляют собой различные формы симметрий – сферическую, радиальную, бирадиальную и билатеральную.

При сферической симметрии, которая имеется только у некоторых групп протозоа (радиолярии, гелиозоа), тело имеет сферическую форму, и части тела расположены концентрически или радиально от центра сферы. У таких животных нет концов или сторон тела и любая плоскость, проходящая через центр, поделит его на эквивалентные половины. Сферический тип симметрии возможен только у очень мелких животных с простой внутренней конструкцией, так как для сферы внутренняя масса, с увеличением внешней поверхности и сложности, растет слишком быстро для эффективного функционирования.

Тело с радиальной симметрией имеет общую форму цилиндра или шара, с центральной осью, от которой расходятся части тела или вдоль которой они расположены регулярно. Основная ось гетерополярна, т.е. с неодинаковыми концами, один из которых несет ротовое отверстие и другой формирует заднюю часть животного. За исключением животных, имеющих нечетное число частей тела, расположенных в циркулярном порядке (морские звезды), любая плоскость, проходящая через ось, делит его на две симметричные части. Животные с тремя, пятью, семью и т.д. частями по кругу имеют симметрию, которую можно называть, соответственно, 3-лучевой, 5-лучевой, 7-лучевой и т.д. (или поворотной). Только определенные плоскости, проходящие через ось, могут поделить такое животное на симметричные половины. Радиальную симметрию находят у кишечнополостных и иглокожих. Однако она не обязательно присуща животному в течение всей его жизни. Личинки офиур, например, имеют зеркальную симметрию, а взрослые особи – симметрию пятого порядка. Надо отметить, что поворотная симметрия пятого порядка особенно часто встречается в органическом мире. У кристаллов имеются поворотные симметрии только 2-го, 3-го, 4-го и 6-го порядков.

В билатеральной симметрии есть две стороны, называемые дорсальной (спина) и вентральной (перед) поверхностями, неодинаковы. Таким образом, только одна срединная продольная, или саггитальная, плоскость симметрии делит билатеральное животное на симметричные половины. Билатеральность присуща большинству животных, включая насекомых, рыб, амфибий, рептилий, птиц, многих ракообразных, млекопитающих.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

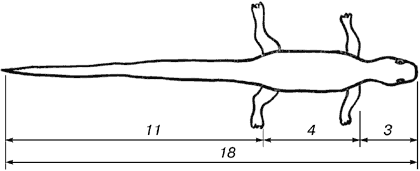
Рис. Ящерица живородящая

1. 2. Симметрия в ботанике

Симметрии также фиксируются и в ботанике. Здесь выделяют радиальную (корни, стебли, цветки), билатеральную (листья), винтовую симметрию подобия (спиральность расположения листьев на стебле, зачатков листьев и цветков на конусе нарастания, цветков в корзинке) и криволинейную (правые и левые листья, семена, плоды, сосуды древесины).

Соразмерные изменения наблюдаются у многих животных и растений. У раковины Turritella duplicata ширина следующих один за другим витков подчиняется закону геометрической прогрессии. Раковина Nautilus являет собой в разрезе логарифмическую спираль – равномерный поворот и растяжение от центра. Семена подсолнуха располагаются по логарифмическим спиралям, образующим два семейства спиралей с противоположным направлением закручивания. Дроби, соответствующие винтообразному расположению листьев на стебле часто являются числами Фибоначчи, которые получаются при разложении в непрерывную дробь иррационального числа, известного под названием “aurea secto” – “золотое сечение”, играющего важную роль в попытках сведения красоты пропорций к некоторой математической формуле.

Образцами орнаментальной (кристаллографической) симметрии являются шестиугольный узор среза паренхимы, некоторые диатомовые водоросли, пчелиные соты, которые “совершенны с точки зрения экономии труда и воска” (Ч.Дарвин).

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения.

1.3. Симметрия тела человека

«Nosce te ipsum» (Познай самого себя)

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».

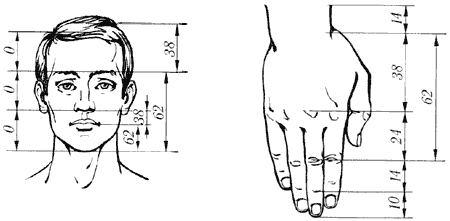
Рис. Золотые пропорции в частях тела человека

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

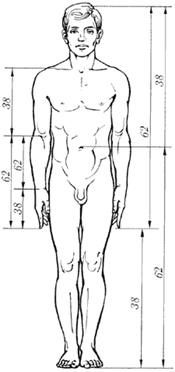
Рис. Золотые пропорции в фигуре человека

⇐ Предыдущая 123 4 Следующая ⇒