
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА И
ПАРАЛЛЕЛЕПИПЕДА
Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
Задание 1. Построить сечение прямоугольного параллелепипеда,
проходящее через три заданные точки А, В, С (рис.1).
| Алгоритм построения сечения параллелепипеда: 1. Провести линию через точки А и С, лежащие на одной грани SS1TT1. Продолжить линию до пересечения с ST (точка М). 2. Провести линию через точки М и B, лежащие на нижней грани PRST. Обозначим К точку пересечения этой линии с ребром SP. 3. Соединить точки КС, лежащие на одной грани. 4. Через точку В провести линию, параллельную КС (свойство параллельных плоскостей). Обозначим Е точку пересечения с ребром R1T1. 5. Соединить точки А и Е. Многоугольник АСКВЕ и есть сечение параллелепипеда. | 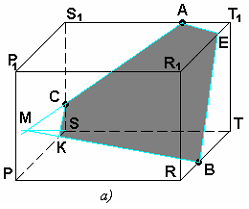 Рис.1. Сечение параллелепипеда.
Рис.1. Сечение параллелепипеда.
|
Задание 2. Построить сечение тетраэдра, проходящее через три заданные точки А, В, С (рис.2).
| Алгоритм построения сечения тетраэдра: 1. Провести линию через точки А и В, лежащие на одной грани TPR. 2. Провести линию через точки В и С, лежащие на нижней грани PRS. Продолжить линию до пересечения с SР (точка М). 3. Соединить точки А и М, лежащие в одной плоскости. Обозначим К — точку пересечения с ребром ТS. 4. Соединить точки КС, лежащие на одной грани. Многоугольник АВСК и есть сечение тетраэдра. | 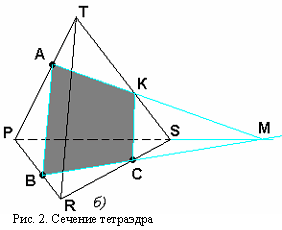
|
Домашнее задание: Построить сечения тетраэдра и параллелепипеда
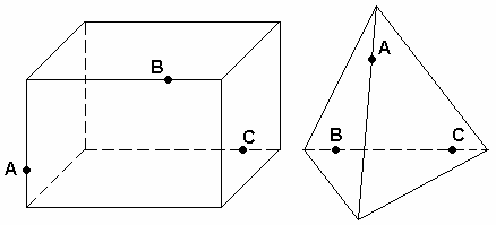
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|