Контакты

Случайная статья

Тема: Примеры решения задач на определение координат центра тяжести составного сечения.

Тема: Примеры решения задач на определение координат центра тяжести составного сечения.

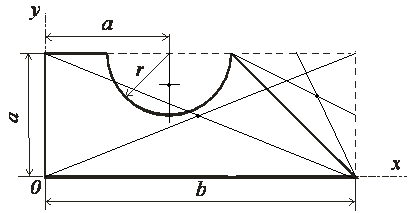
Пример 1.Определить координаты центра тяжести плоской фигуры, изображённой на рисунке 2, если известно a = 40 см, b =100 см, r = 20 см .

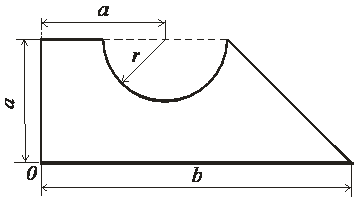
Рис. 2 - Схема задачи

Решение:

1. Разбиваем чертёж фигуры на простейшие составные части: прямоугольник, треугольник, полукруг, обозначаем центр тяжести каждой из них и располагаем чертёж фигуры в первой четверти координатных осей (рис. 3).

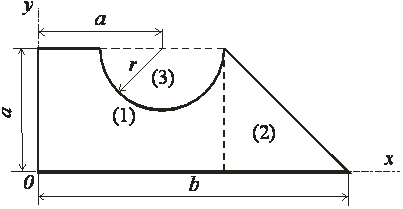
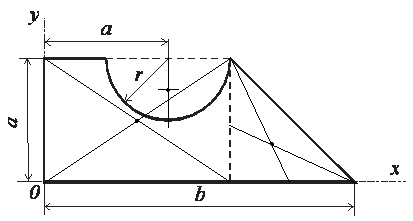
Рис. 3 - Разбиение на части

2. Заполняем таблицу

31,5

а) Площади сечения простейших фигур

для прямоугольника А₁ = 40 × 60 = 2400 см²

для треугольника А₂ = 40 × 40 / 2 = 800 см²

для полукруга А₁ = p × 20² / 2 = 628 см²

б) Центры тяжестей рассматриваемых частей фигуры имеют следующие координаты:

для прямоугольника х₁= 30 см, y₁= 20 см;

для треугольника х₂= 60+40/3=73,3 см, y₂= 40/3=13,3 см;

для полукруга х₃= 40 см, y₃= 40-4·20/(3·π) =31,5 см.

3. Вычисляем координаты центра тяжести фигуры по формулам

Х_с = (2400×30 + 800×73,3 - 628×40) / (2400 + 800 - 628) = 41 см

Y_c = (2400×20 + 800×13,3 - 628×31,5) / (2400 + 800 - 628) = 15,1 см

Ответ: С (41;15,1)

Проверка:

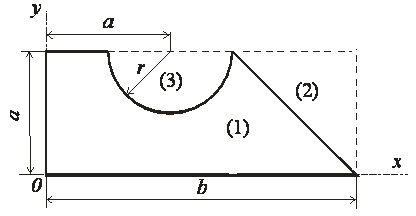
Х_с = (4000×50 - 800×86,7 - 628×40) / (4000 - 800 - 628) = 41 см

Y_c = (4000×20 - 800×26,7 - 628×31,5) / (4000 - 800 - 628) = 15,1 см

Ответ: С (41;15,1)

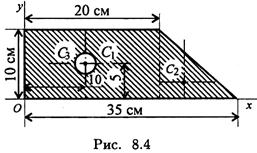
Задача 1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.

Разбиваем фигуру на три части:

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.