Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Примечание 1.

Стр 1 из 2Следующая ⇒

1.Найдите значение выражения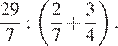

Решение.

Найдём значение выражения:

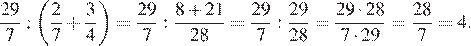
Ответ: 4.

Найдите значение выражения .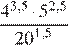

Решение.

Выполним преобразования:

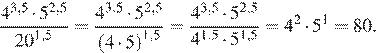
Ответ: 80.

3.Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 22 500 рублей. Какую сумму он получит после уплаты налогов? Ответ дайте в рублях.

Решение.

После уплаты 13% налога останется 87% зарплаты или 22 500 · 0,87 = 19 575 руб.

4.Среднее гармоническое трёх чисел 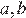и 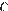вычисляется по формуле 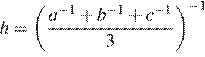. Найдите среднее гармоническое чисел 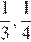и .

Решение.

Найдём среднее гармоническое чисел:

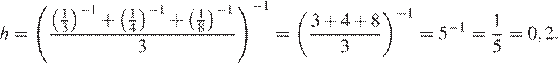
Ответ: 0,2.

5.Найдите значение выражения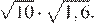

Решение.

Найдём значение выражения:

Ответ: 4.

6.В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.

Решение.

Расход воды составил 114 − 103 = 11 куб. м. Поэтому Алексей должен заплатить 11 · 19,2 = 211,2 руб.

Ответ: 211,2.

7.Найдите корень уравнения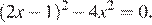

Решение.

Последовательно получаем:

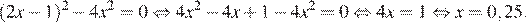
Ответ: 0,25.

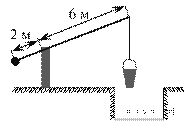
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?

Решение.

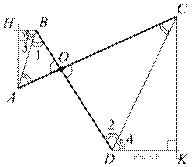
Введём обозначения, как показано на рисунке. Здесь AC — положение «журавля» до опускания, BD — положение после опускания, AH — высота, на которую поднялся конец короткого плеча, CK — высота, на которую опустился конец длинного.

В равнобедренных треугольниках AOB и COD углы AOB и COD, противолежащие основаниям, равны как вертикальные, поэтому равны и углы при их основаниях. Тем самым, эти треугольники подобны по двум углам, и

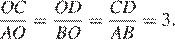
Накрест лежащие углы 1 и 2, образованные при пересечении секущей BD прямых AB и CD, равны, поэтому прямые AB и CD параллельны. Тогда стороны углов 3 и 4 попарно параллельны, а значит, эти углы равны.

Следовательно, прямоугольные треугольники AHB и CDK подобны, поскольку имеют равные острые углы. Имеем:

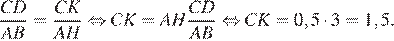
Ответ: 1,5.

Примечание 1.

Можно привести несколько иное доказательство подобия треугольников 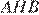и 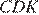. На приведённой ниже картинке есть два маленьких треугольника обозначенные и 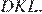Они прямоугольные и одна пара углов равна друг другу как накрест лежащие при параллельных прямых. Поэтому они подобны.

Затем, можно заметить, что у треугольников и 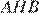соответственные углы равны друг другу (потому, что их стороны параллельны), следовательно, треугольники подобны. Аналогично с треугольникам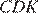и и 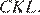Из трёх пар подобий этих треугольников следует, что треугольник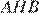и и 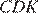подобны.

12 Следующая ⇒