
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ. Модель парной линейной регрессии.. Решение
Федеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт цветных металлов и материаловедения
Кафедра АППТМ
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ
Модель парной линейной регрессии
Преподаватель ________ Т.В. Пискажова
Студент МЦ15-15 ________ А.А. Потапчик
Красноярск 2015
Модель парной линейной регрессии.
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость. Сопоставить в отчете коэффициенты, рассчитанные по формулам 1.1-1.6 и функциями Microsoft Excel. Рассчитать также для одного столбца дисперсию по формуле 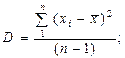
2. Построить линейное уравнение парной регрессии y(x), рассчитав коэффициенты регрессии. Сделать рисунок с помощью точечной диаграммы с выводом уравнения тренда и коэффициента R2. Оценить статистическую значимость параметров регрессии.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Проверить качество уравнения регрессии при помощи F-критерия Фишера. Сверить полученные коэффициенты и оценки с результатами «Анализ Данных. Регрессия» Microsoft Excel!
4. Выполнить прогноз показателя y при прогнозном значении x, составляющем 101-105% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a=0,05.
Решение
1. Для определения степени тесноты связи обычно используют линейный коэффициент корреляции:
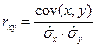 ,
,
где 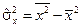 ,
, 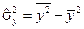 – выборочные дисперсии переменных x и y,
– выборочные дисперсии переменных x и y, 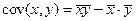 – ковариация признаков. Соответствующие средние определяются по формулам:
– ковариация признаков. Соответствующие средние определяются по формулам:
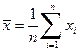 , ,
| 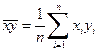 , ,
|
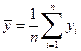 , ,
| 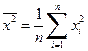 . .
|
Для расчета коэффициента корреляции (1.1) строим расчетную таблицу (табл. 1.2):
Таблица 1.1
| Номер пробы | Высота настыля, см | Куски, шт | xy | x2 | y2 | y(x) | e=y-y(x) | e2 |
| x | y | |||||||
| 40,2 |
256,1
246,6244
9,5
89,78673
319,4
210,5458
108,9
11849,25
302,6
231,2694
71,3
5088,053
206,1
242,7706
-36,7
1344,735
246,0
192,4812
53,5
2864,259
226,8
180,6266
46,2
2131,979
182,3
174,5525
7,7
60,02413
135,1
131,4345
3,7
13,43606
99,6
130,5234
-30,9
956,2575
98,1
131,8827
-33,8
1141,27
117,5
141,5529
-24,1
578,542
115,9
206,2504
-90,4
8163,203
178,7
142,0382
36,7
1344,085
212,3
213,736
-1,4
2,062164
210,4
212,7167
-2,3
5,367292
198,7
192,4781
6,2
38,71253
249,3
168,8605
80,4
6470,518
139,9
222,3359
-82,4
6795,686
217,2
241,8416
-24,6
607,2106
132,1
264,2668
-132,2
17468,07
149,1
194,9818
-45,9
2105,142
159,7
270,1377
-110,4
12196,48
160,8
274,8277
-114,0
13002,33
159,0
233,7235
-74,7
5583,599
202,9
262,2417
-59,3
3521,434
212,1
210,7983
1,3
1,694374
229,2
237,7367
-8,5
72,87549
221,6
240,0218
-18,4
339,3611
170,8
200,6348
-29,8
890,1135
266,8
226,1749
40,6
1650,395
251,3
301,0287
-49,7
2472,945
191,1
348,447
-157,3
24758,08
256,8
314,0912
-57,3
3282,284
253,9
341,0598
-87,2
7596,831
322,8
358,5914
-35,8
1281,028
363,3
282,2777
81,0
6564,608
489,1
401,2122
87,9
7724,266
531,0
346,9797
184,0
33863,47
375,5
262,0971
113,4
12860,22
336,0
239,8252
96,2
9249,59
339,1
267,1454
72,0
5177,462
381,2
343,9532
37,2
1387,327
375,9
420,1442
-44,2
1957,547
444,1
440,2919
3,8
14,50187
401,9
438,7847
-36,9
1360,479
366,7
299,4286
67,3
4525,437
443,6
318,9663
124,6
15533,57
382,8
353,6541
29,1
849,4824
391,2
454,8213
-63,6
4047,672
487,3
445,2511
42,0
1768,109
469,3
421,8818
47,4
2248,487
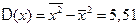 ,
, 
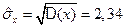 ,
, 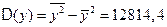 ,
, 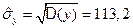 ,
,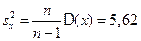 ,
, 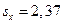 ,
,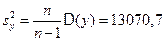 ,
, 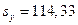 ,
,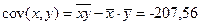 ,
, 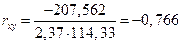 .
. 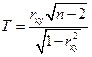 ,
,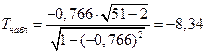 и
и 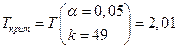 .
.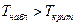 , то коэффициент корреляции существенно отличается от нуля и значит наш коэффициент корреляции является статистически значимым.
, то коэффициент корреляции существенно отличается от нуля и значит наш коэффициент корреляции является статистически значимым.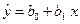 , (1.7)
, (1.7)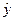 была минимальной:
была минимальной: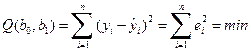 , (1.8)
, (1.8) – отклонения yi от оцененной линии регрессии. Необходимым условием существования минимума функции двух переменных (1.8) является равенство нулю ее частных производных по неизвестным параметрам b0 и b1. В результате получаем систему нормальных уравнений:
– отклонения yi от оцененной линии регрессии. Необходимым условием существования минимума функции двух переменных (1.8) является равенство нулю ее частных производных по неизвестным параметрам b0 и b1. В результате получаем систему нормальных уравнений: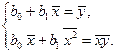
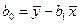 , (1.9)
, (1.9)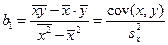 . (1.10)
. (1.10)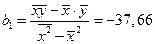 ;
;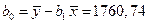 .
.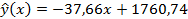 (1,11)
(1,11)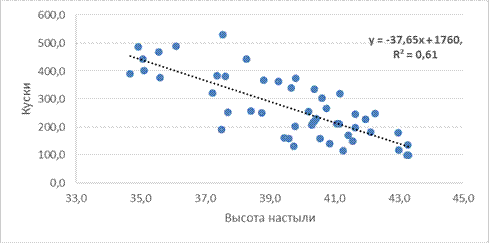
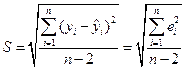 . (1.12)
. (1.12)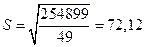 .
.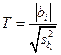 , = (1.13)
, = (1.13)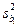 – дисперсия коэффициента регрессии.
– дисперсия коэффициента регрессии.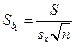 . (1.14)
. (1.14)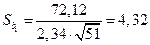
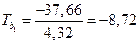 .
.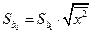 . (1.15)
. (1.15)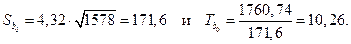
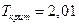 . Поскольку по модулю
. Поскольку по модулю 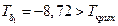 и
и 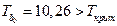 , то коэффициенты регрессии значимо отличаются от нуля.
, то коэффициенты регрессии значимо отличаются от нуля.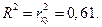
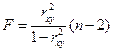 , (1.16)
, (1.16)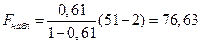 .
.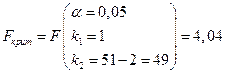
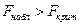 , то признается статистическая значимость построенного уравнения регрессии.
, то признается статистическая значимость построенного уравнения регрессии.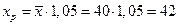 , тогда прогнозное значение количества кусков:
, тогда прогнозное значение количества кусков: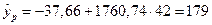
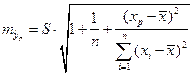 . (1.17)
. (1.17)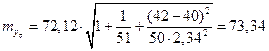
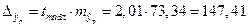 .
.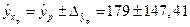 ,
,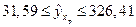 .
.