Математика 19 группа урок 15.12.2020

Математика 19 группа урок 15.12.2020

Тема: Урок одной задачи.

Задания:

1. Вам представлено решение первой задачи. Переписать в тетрадь.

2. Решить задачу 1.1 – там только поменять числа.

3. Решить задачу 1.2 – меняются обозначения.

Задача 1. Прямая ВD перпендикулярна к плоскости треугольника АВС. Известно, что ВD = 9, АС = 6, ВС = ВА = 5. Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника АСD

Дано: Прямая ВD перпендикулярна к плоскости ΔАВС. ВD = 9, АС = 6, ВС = ВА = 5.

Найти: а) расстояние от точки D до прямой АС; б) площадь ΔАСD.

Решение:

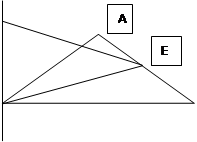
а) Так как в ΔАВС ВС = ВА, значит этот треугольник равнобедренный. Проведем в нем высоту ВЕ, она же будет медианой (т.е. точка Е – середина отрезка АС).

По теореме о трех перпендикулярах DЕ – перпендикуляр к АС, значит DЕ - расстояние от точки D до прямой АС.

(самостоятельно покажите на рисунке прямые углы и известные отрезки)

Из ΔВЕС, <Е = 90⁰ ВС = 5, ЕС = 3 (АС/2 = 6/2), значит ВЕ = 4 (первая Пифагорова тройка).

Из ΔВЕD, <В = 90⁰ по теореме Пифагора DE² = BD² + BE²,

DE² = 9² + 4²

DE² = 81 + 16

DE² = 97

DE = √97

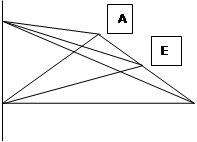
б)

S(ΔАСD) = ½*AC*DE = ½*6*√97 = 3√97

Ответ: а) √97, б) 3√97.

Решить самостоятельно:

Задача 1.1 Прямая ВD перпендикулярна к плоскости треугольника АВС. Известно, что ВD = 8, АС = 16, ВС = ВА = 10. Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника АСD.

Задача 1.2 Прямая МК перпендикулярна к плоскости треугольника МNР. Известно, что МК = 9, NР = 6, МN = МР = 5. Найдите: а) расстояние от точки К до прямой NР; б) площадь треугольника NРК.