ВЯТСКИЙ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

ВЯТСКИЙ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра Информатика и вычислительная техника

Предмет: Математическое и имитационное моделирование

Контрольная работа № 1

Вариант № 1

Студент: 3 курса, группы ИВТс-33

Ф.И.О.: Тестов Г. Н.

Преподаватель:

Дата сдачи работы «___» __________ 2015 г.

Оценка: _______________

Проверил:_______________

Киров

Оглавление

Задание 1. Построить модель варианта q-схемы и обеспечить сбор статистических данных о процессе функционирования исследуемого в работе варианта системы. 3

Задание 2 Планирование машинных экспериментов с имитационными моделями систем массового обслуживания. 10

Задание 3 «Динамические модели». 16

СПИСОК литературы.. 18

Вариант 1

Задание 1. Построить модель варианта q-схемы и обеспечить сбор статистических данных о процессе функционирования исследуемого в работе варианта системы.

Вариант	Схема	Параметры	Т, ед.вр.
	а	На схеме

Рис.1. Q-схема

Исходя из заданных условий и необходимости обеспечения ограничений по загрузке системы ρ=1, получаем

, ед. вр.

Таким образом, для данной Q-схемы после подстановки исходных данных имеем 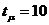ед. вр.

Блок–диаграмма GPSS модели процесса функционирования исследуемой Q-схемы

Текст программы моделирования Q-схемы

010 SIMULATE

020 EXPON FUNCTION RN1,C24

0,0/.100,.104/.200,.222/.300,.355/.400,.509

.500,.690/.600,.915/.700,1.200/.750,1.380

.800,1.600/.840,1.830/.880,2.120/.900,2.300

.920,2.520/.940,2.810/.950,2.990/.960,3.200

.970,3.500/.980,3.900/.990,4.600/.995,5.300

.998,6.200/.999,7/1,8

090 GENERATE 10,FN$EXPON

100 QUEQUE 1

110 SEIZE 1

120 DEPARTURE 1

130 ADVANCE 10,FN$EXPON

140 RELEASE 1

150 TERMINATE

160 GENERATE 1000

170 TERMINATE 1

Результаты моделирования Q-схемы

GPSS World Simulation Report – 1

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 1000.000 9 1 0

NAME VALUE

EXPON 10000.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE 104 0 0

2 QUEUE 104 7 0

3 SEIZE 97 0 0

4 DEPART 97 0 0

5 ADVANCE 97 1 0

6 RELEASE 96 0 0

7 TERMINATE 96 0 0

8 GENERATE 1 0 0

9 TERMINATE 1 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

1 97 0.982 10.124 1 98 0 0 0 7

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

1 13 7 104 3 6.684 64.273 66.182 0

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

106 0 1002.090 106 0 1

98 0 1004.696 98 5 6

107 0 2000.000 107 0 8

Задание 2. Исследовать на машинной модели q-схему на рис. 2. Предполагается, что интервалы времени между моментами поступления заявок и источников И1 и И2 имеют экспоненциальное распределение, а время обслуживания в каналах К1, К2, К3 постоянно. Интенсивности обслуживания µ, ед./ед. вр. представлены в табл. 2. Необходимо провести моделирование процесса функционирования схемы на интервале времени Т, ед.вр.

Рис.2. Двухфазная двуканальная СМО с двумя потоками входящих заявок

Варианты задания ко второй части задачи 1

Вариант	λ₁	λ₂	Т	L₁	L₂	L₃	L₄	µ₁	µ₂	µ₃

Необходимо провести моделирование процесса функционирования данной схемы на интервале времени (0,Т).

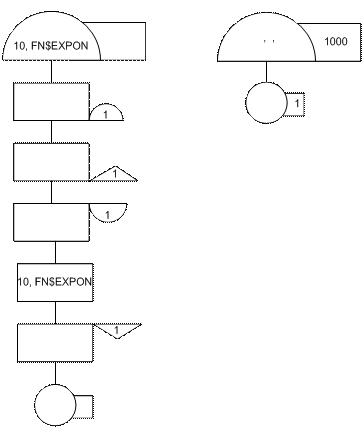
Блок–диаграмма GPSS модели процесса функционирования исследуемой Q –схемы

Текст программы моделирования Q-схемы

010 SIMULATE

020 EXPON FUNCTION RN1,C24

0,0/.100,.104/.200,.222/.300,.355/.400,.509

.500,.690/.600,.915/.700,1.200/.750,1.380

.800,1.600/.840,1.830/.880,2.120/.900,2.300

.920,2.520/.940,2.810/.950,2.990/.960,3.200

.970,3.500/.980,3.900/.990,4.600/.995,5.300

.998,6.200/.999,7/1,8

090 SVE1 EQU 1

100 SVE2 EQU 2

110 SVE3 EQU 3

120 SVE4 EQU 4

130 SVE1 STORAGE 10

140 SVE2 STORAGE 11

150 SVE3 STORAGE 12

160 SVE4 STORAGE 13

170 GENERATE 21,FN$EXPON

180 ASSIGN 1,1

190 ENTER 1,1

200 TRANSFER ,WAY

210 GENERATE 41,FN$EXPON

220 ASSIGN 1,2

230 ENTER 2,1

240 WAY SEIZE 1

250 LEAVE P1

260 ADVANCE 23

270 RELEASE 1

280 TEST E P1,1,KAN3

290 ENTER 3,1

300 SEIZE 2

310 LEAVE 3,1

320 ADVANCE 14

330 RELEASE 2

340 TERMINATE

350 KAN3 ENTER 4,1

360 SEIZE 3

370 LEAVE 4,1

380 ADVANCE 25

390 RELEASE 3

400 TERMINATE

410 GENERATE 1,,1000

420 TERMINATE 1

430 START 1

Результаты моделирования Q-схемы

GPSS World Simulation Report

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 1000.000 26 3 4

NAME VALUE

EXPON 10000.000

KAN3 19.000

SVE1 1.000

SVE2 2.000

SVE3 3.000

SVE4 4.000

WAY 8.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE 55 0 0

2 ASSIGN 55 14 0

3 ENTER 41 0 0

4 TRANSFER 41 10 0

5 GENERATE 22 0 0

6 ASSIGN 22 0 0

7 ENTER 22 10 0

WAY 8 SEIZE 43 0 0

9 LEAVE 43 0 0

10 ADVANCE 43 1 0

11 RELEASE 42 0 0

12 TEST 42 0 0

13 ENTER 30 0 0

14 SEIZE 30 0 0

15 LEAVE 30 0 0

16 ADVANCE 30 0 0

17 RELEASE 30 0 0

18 TERMINATE 30 0 0

KAN3 19 ENTER 12 0 0

20 SEIZE 12 0 0

21 LEAVE 12 0 0

22 ADVANCE 12 0 0

23 RELEASE 12 0 0

24 TERMINATE 12 0 0

25 GENERATE 1 0 0

26 TERMINATE 1 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

1 43 0.983 22.849 1 44 0 0 0 20

2 30 0.420 14.000 1 0 0 0 0 0

3 12 0.300 25.000 1 0 0 0 0 0

STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY

SVE1 10 0 0 10 41 1 7.376 0.738 0 14

SVE2 11 1 0 10 22 1 3.891 0.354 0 0

SVE3 12 12 0 1 30 1 0.000 0.000 0 0

SVE4 13 13 0 1 12 1 0.006 0.000 0 0

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

81 0 1001.000 81 0 25

44 0 1006.482 44 10 11 1 1.000

79 0 1027.753 79 0 5

80 0 1046.591 80 0 1

Задание 2 Планирование машинных экспериментов с имитационными моделями систем массового обслуживания

Провести анализ влияния экзогенных переменных модели системы, формализованной в виде Q-схемы, на эндогенные переменные с построением плана эксперимента при использовании метода наименьших квадратов и линейного регрессионного анализа.

Объект моделирования – Q-схема

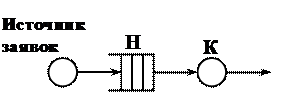
при следующих условиях:

§ на вход системы поступает простейший поток заявок с плотностью λ;

§ заявка, заставшая канал обслуживания занятым, становится в очередь и ожидает, пока канал не освободится;

§ емкость накопителя (максимальная длина очереди) равна L;

§ время обслуживания заявки имеет показательное распределение с параметром μ;

§ время ожидания заявки не ограничено.

1. Записать формальную постановку задачи в соответствии с номером своего варианта (таблица 3).

2. Подготовить исходные данные и построить план машинного эксперимента.

3. Составить программу на языке GPSS World, реализующую имитационную модель функционирования СМО.

4. Провести машинный эксперимент в соответствии с построенным планом и сравнить результаты с неуправляемым экспериментом.

Вариант	Переменные
	Экзогенные			Эндогенные
	λ, заявок/мин	μ, заявок/мин	L
	+	+	+	Среднее время нахождения в системе

Пусть исследуется одноканальная Q-схема со следующими параметрами:

интенсивность поступления заявок λ = 7 заявок/мин;

интенсивность обслуживания заявок μ = 10 заявок/мин;

емкость накопителя L = 8.

Необходимо оценить среднее время нахождения заявки в системе (время ожидания + время обслуживания) при минимальных затратах машинных ресурсов.

Необходимо определить влияние факторов, находящихся в функциональной связи с искомой характеристикой:

отобрать факторы, влияющие на искомую характеристику,

описать функциональную зависимость,

определить уровни выбранных факторов.

Для составления плана эксперимента выделим следующие факторы:

интенсивность поступления заявок х₁ = λ;

интенсивность обслуживания заявок х₂ = μ;

емкость накопителя х₃ = L.

Определим локальную подобласть планирования эксперимента путем выбора основного (нулевого) уровня х_i₀ и интервалов варьирования Δx_i для каждого фактора.

Факторы	Уровни факторов		Интервалы варьирования
Факторы	–1	+1	Интервалы варьирования
х₁
х₂
х₃

Для определения зависимости между уровнями факторов и реакцией системы

построим математическую модель планирования в виде алгебраического полинома

Для оценки коэффициентов модели используем план ПФЭ типа 2^k.

Матрица планирования:

Номер опыта	План ПФЭ								Реакция у
Номер опыта									Реакция у
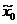
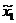
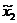
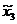
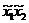
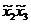
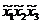
	+1	–1	–1	–1	+1	+1	+1	–1	у₁
	+1	–1	–1	+1	+1	–1	–1	+1	у₂
	+1	–1	+1	–1	–1	+1	–1	+1	у₃
	+1	–1	+1	+1	–1	–1	+1	–1	у₄
	+1	+1	–1	–1	–1	–1	+1	+1	у₅
	+1	+1	–1	+1	–1	+1	–1	–1	у₆
	+1	+1	+1	–1	+1	–1	–1	–1	у₇
	+1	+1	+1	+1	+1	+1	+1	+1	у₈

Будем считать, что эффектами взаимодействия факторов можно пренебречь, и будем рассматривать линейную модель

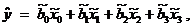
при этом положим 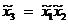и .

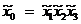Получим план ДФЭ типа 2^3-1, что позволит сократить число опытов в два раза.

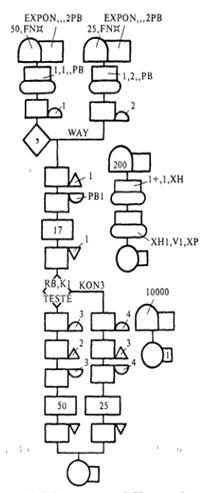
Блок–диаграмма GPSS–модели Q–схемы

Номер опыта	,				Реакция у
Номер опыта					Реакция у
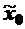
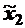
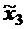
	+1	–1	–1	+1	у₁	0,2
	+1	+1	+1	+1	у₂	0,333
	+1	+1	–1	–1	у₃
	+1	–1	+1	–1	у₄	0,143

Проведение опыта в i-й точке факторного пространства:

- по нормированным значениям факторов i-й строки плана эксперимента определяем натуральные значения координат;

- факторы устанавливаем на уровни, соответствующие полученным координатам;

- по результатам машинного эксперимента определяем отклик (реакцию) системы у_i .

В таблице выше приведены значения реакции Q-схемы на выбранных уровнях факторов, вычисленные в соответствии с формулой

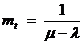
(при µ > λ).

Используя метод наименьших квадратов, определим коэффициенты регрессионной модели.

Для этого необходимо решить задачу

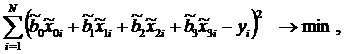
где N – число опытов.

Приравнивая частные производные по переменным 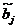к нулю, получим систему уравнений:

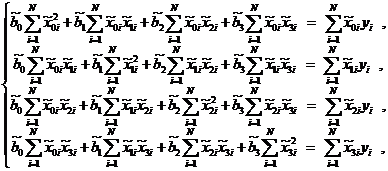
причем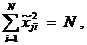

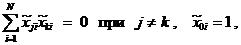
поэтому

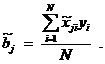
Составив программу для вычисления коэффициентов 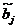, проведем вычисления и получим следующую модель:

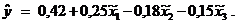
Учитывая, что

и подставляя соответствующие значения, окончательно получим:

Анализ полученного результата:

- на реакцию системы (время нахождения в системе заявки) наиболее сильно влияет фактор x₂ (интенсивность обслуживания заявок); почти такое же (по степени воздействия) влияние оказывает фактор x₁ (интенсивность поступления заявок); влияние фактора x₃ (емкость накопителя) намного слабее;

- знаки перед коэффициентами при x_i указывают, что при увеличении фактора x₁ реакция системы возрастает, а при увеличении x₂ – убывает.

Анализ проведенного планируемого эксперимента показывает:

для получения одних и тех же результатов (среднего времени нахождения заявки в системе) без использования методов планирования эксперимента необходимо провести восемь опытов; с учетом построенного плана ДФЭ – достаточно четырех опытов (в два раза меньше).

Задание 3 «Динамические модели»

Задания поступают на станок в среднем один раз в час. Распределение величины интервала между ними экспоненциально. При нормальном режиме работы задания выполняются в порядке их поступления. Перед выполнением задания производится наладка станка, время осуществления которой распределено равномерно на интервале 0.2-0.5 ч. Время выполнения задания нормально распределено с математическим ожиданием 0.5 ч и среднеквадратичным отклонением 0.1 ч. Станок подвергается поломкам, при которых он не может продолжать выполнения задания. Интервалы между поломками распределены нормально с математическим ожиданием 20 ч и среднеквадратичным отклонением 2 ч. При поломке выполняемое задание удаляется со станка и помещается в начало очереди заданий к станку. Общая продолжительность устранения поломки распределено равномерно на интервале от 0.1 до 0.5 часа. Проанализируйте работу станка в течение обработки 500 деталей для получения информации по загрузке станка и времени выполнения задания.

Текст программы моделирования Q-схемы

010 EXPON FUNCTION RN1,C24

0,0/.100,.104/.200,.222/.300,.355/.400,.509

.500,.690/.600,.915/.700,1.200/.750,1.380

.800,1.600/.840,1.830/.880,2.120/.900,2.300

.920,2.520/.940,2.810/.950,2.990/.960,3.200

.970,3.500/.980,3.900/.990,4.600/.995,5.300

.998,6.200/.999,7/1,8

090 GENERATE 60,FN$EXPON

100 MQUE QUEUE 1

110 SEIZE 1

120 DEPART 1

130 ADVANCE 21,9

140 ADVANCE 30,FN$EXPON

150 TRANSFER .00083,,MGOOD

160 ADVANCE 18,12

170 RELEASE 1

180 TRANSFER 1,,MQUE

190 MGOOD RELEASE 1

200 TERMINATE

210 GENERATE 500

220 TERMINATE 1

230 START 1

Результаты моделирования Q-схемы

GPSS World Simulation Report

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 500.000 14 1 0

NAME VALUE

EXPON 10000.000

MGOOD 11.000

MQUE 2.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE 3 0 0

MQUE 2 QUEUE 3 2 0

3 SEIZE 1 0 0

4 DEPART 1 0 0

5 ADVANCE 1 0 0

6 ADVANCE 1 1 0

7 TRANSFER 0 0 0

8 ADVANCE 0 0 0

9 RELEASE 0 0 0

10 TRANSFER 0 0 0

MGOOD 11 RELEASE 0 0 0

12 TERMINATE 0 0 0

13 GENERATE 1 0 0

14 TERMINATE 1 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

1 1 0.635 95.177 1 1 0 0 0 2

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

1 2 2 3 1 0.889 44.445 66.667 0

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

1 0 164.956 1 6 7

5 0 263.371 5 0 1

6 0 300.000 6 0 13

Список литературы

1. Емельянов А.А. Имитационное моделирование экономических процессов: учеб. пособие / А.А. Емельянов, Е.А. Власова, Р.В. Дума / Под ред. А.А. Емельянова. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2006. - 416 с.

2. Советов Б.Я. Моделирование систем: лабораторный практикум / Б.Я. Советов, С.А. Яковлев. – М.: ВШ, 2010. – 340 с.