
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
| № | Виды интегралов | Рекомендации по решению |
| 1. |  ,
где R – дробно-рациональное выражение, содержащее ,
где R – дробно-рациональное выражение, содержащее 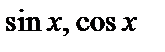 в нечетных степенях. в нечетных степенях.
| Интегрируем с помощью универсальной подстановки:
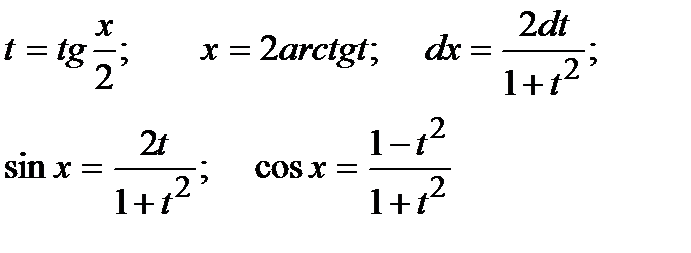
|
| 2. | 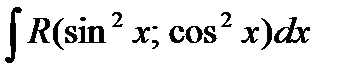 ,
где R – дробно-рациональное выражение, содержащее ,
где R – дробно-рациональное выражение, содержащее 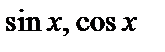 в четных степенях. в четных степенях.
| Интегрируем с помощью подстановки:
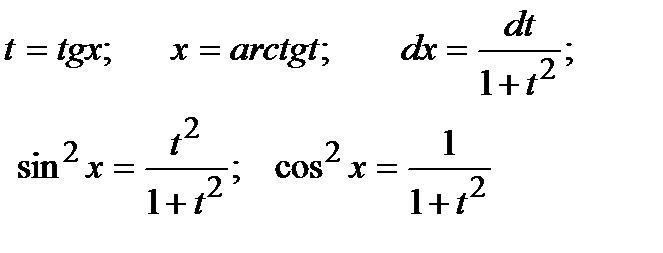
|
| 3а) | 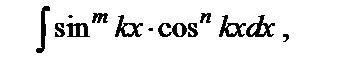 Если одна из степеней m или n (или и та, и другая) – нечетные числа;
Если одна из степеней m или n (или и та, и другая) – нечетные числа;
| Интегрируем с помощью метода подведения под знак дифференциала, используя тождества:
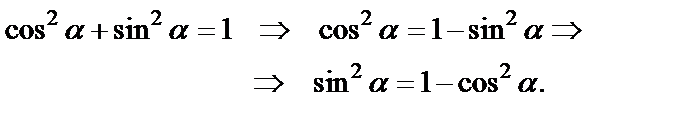 От множителя стоящего в нечетной степени отделяем один сомножитель и подводим под дифференциал.
От множителя стоящего в нечетной степени отделяем один сомножитель и подводим под дифференциал.
|
| 3б) | 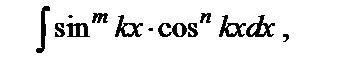 Если степени и m, и n – четные неотрицательные числа
Если степени и m, и n – четные неотрицательные числа
| Используем формулы понижения степени :
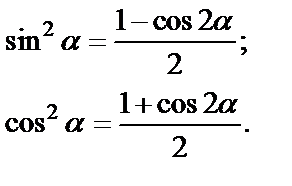 Иногда целесообразно воспользоваться формулой:
Иногда целесообразно воспользоваться формулой: 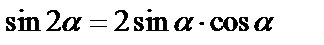 . .
|
| 3в) | 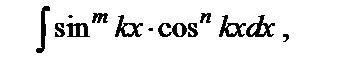 Если степени и m, и n – четные числа, а хотя бы одна из них отрицательная (m или n, или обе).
Если степени и m, и n – четные числа, а хотя бы одна из них отрицательная (m или n, или обе).
| Интегрируем с помощью метода подстановки, используя формулы:
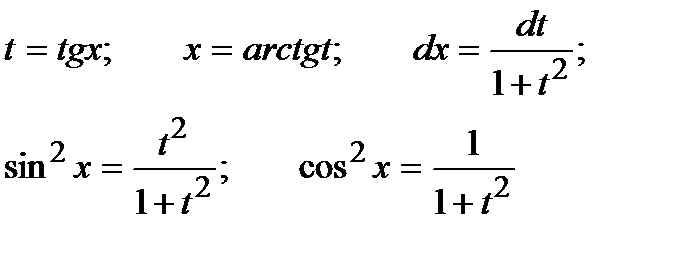
|
| 4. |
 где n – целое положительное число, k – действительное число.
где n – целое положительное число, k – действительное число.
| Решаем методом подстановки:
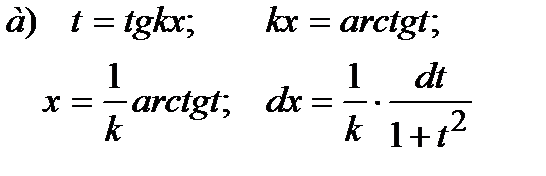 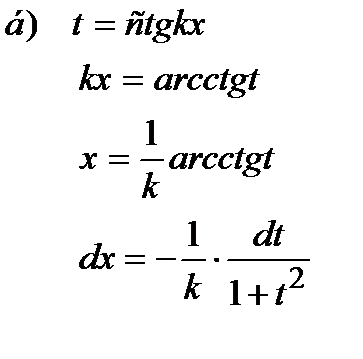
|
| 5. |
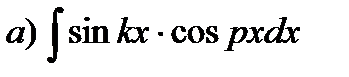
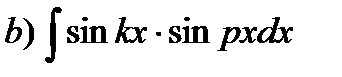
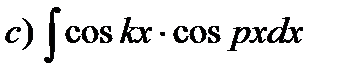 где k, p – различные действительные числа.
где k, p – различные действительные числа.
| Используем тригонометрические формулы:
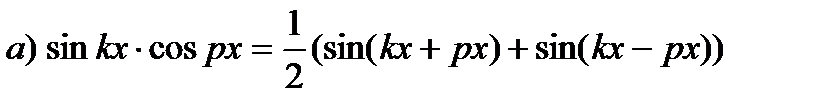
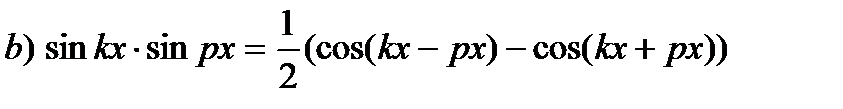
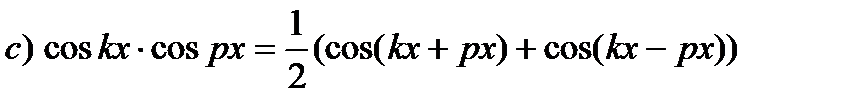
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|