- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
основных методов интегралов)
Обзоры методов интегрирования
(основных методов интегралов)
| № п/п | Вид интеграла | Метод интегрирования | ||||||

| Подстановка 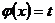 . .
| |||||||
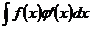
| Интегрирование по частям 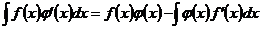
| |||||||
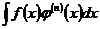
| Сводится к интегрированию произведения 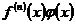 с помощью формулы кратного интегрирования по частям: с помощью формулы кратного интегрирования по частям:
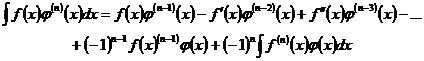
| |||||||
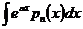
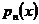 - многочлен степени - многочлен степени 
| Применяя формулу кратного интегрирования по частям (см. п. 3), получим
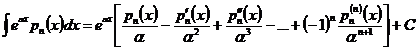
| |||||||
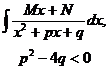
| Подстановка 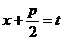 . .
| |||||||
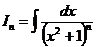
| Применение рекуррентной формулы
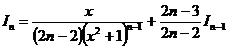 . .
| |||||||
 , где , где 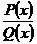 - правильная рациональная дробь, - правильная рациональная дробь, 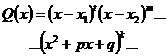
| Подынтегральную дробь представляют в виде суммы простейших дробей

| |||||||
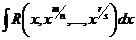 , где , где 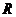 - рациональная функция своих аргументов - рациональная функция своих аргументов
| Приводится к интегралу от рациональной дроби подстановкой 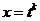 , где , где 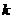 - общий знаменатель дробей - общий знаменатель дробей
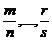 . .
| |||||||
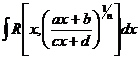 , где , где 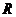 - рациональная функция своих аргументов - рациональная функция своих аргументов
| Приводится к интегралу от рациональной дроби подстановкой
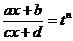 . .
| |||||||
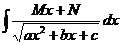
| Подстановкой 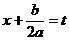 интеграл приводится к сумме двух интегралов: интеграл приводится к сумме двух интегралов: 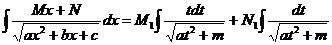 Первый интеграл сводится к интегралу от степенной функции, а второй интеграл табличный.
Первый интеграл сводится к интегралу от степенной функции, а второй интеграл табличный.
| |||||||
| № п/п | Вид интеграла | Метод интегрирования | ||||||
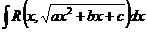 , где , где 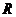 - рациональная функция своих аргументов - рациональная функция своих аргументов
| Приводится к интегралу от рациональной дроби подстановками Эйлера:
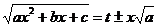 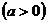 , , 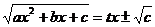 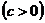 , ,
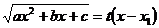 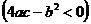 ,
где ,
где 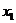 - корень трехчлена - корень трехчлена 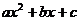 .
Для вычисления данного интеграла применяются также тригонометрические подстановки: .
Для вычисления данного интеграла применяются также тригонометрические подстановки:
| |||||||
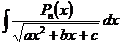 ,
где ,
где 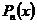 - многочлен степени - многочлен степени 
| Записываем равенство
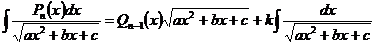 ,
где ,
где  - многочлен степени - многочлен степени 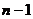 . Дифференцируя обе части этого равенства и умножая на . Дифференцируя обе части этого равенства и умножая на 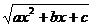 , получим тождество , получим тождество
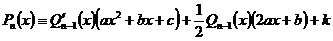 ,
которое дает систему ,
которое дает систему 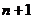 линейных уравнений для определения коэффициентов многочлена линейных уравнений для определения коэффициентов многочлена  и множителя и множителя 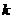 .
Интеграл же .
Интеграл же 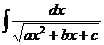 берется методом указанным в п. 10
( берется методом указанным в п. 10
( 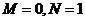 ). ).
| |||||||
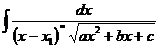
| Этот интеграл приводится подстановкой 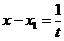 к интегралу, рассмотренному выше. к интегралу, рассмотренному выше.
| |||||||
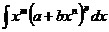 ,
где ,
где 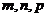 -рациональные числа (интеграл от биномиального дифференциала). -рациональные числа (интеграл от биномиального дифференциала).
| Интеграл от биномиального дифференциала выражается через элементарные функции только при выполнении одного из следующих условий:
1) если 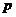 - целое число,
2) если - целое число,
2) если 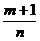 - целое число,
3) - целое число,
3) 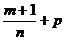 - целое число.
1-й случай
а) если - целое число.
1-й случай
а) если 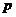 - целое положительное число, то нужно раскрыть - целое положительное число, то нужно раскрыть
| |||||||
| № п/п | Вид интеграла | Метод интегрирования | ||||||
скобки 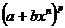 по биному Ньютона и вычислить интегралы от степеней.
б) если по биному Ньютона и вычислить интегралы от степеней.
б) если 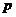 - целое отрицательное число, то подстановка - целое отрицательное число, то подстановка 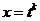 , где , где 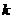 - общий знаменатель дробей - общий знаменатель дробей 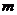 и и  , приводит к интегралу от рациональной дроби;
2-й случай
если , приводит к интегралу от рациональной дроби;
2-й случай
если 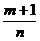 - целое число, то применяется подстановка - целое число, то применяется подстановка  , , 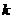 - знаменатель дроби - знаменатель дроби 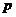 ;
3-й случай
если ;
3-й случай
если 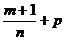 - целое число, то применяется подстановка - целое число, то применяется подстановка 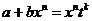 , , 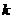 - знаменатель дроби - знаменатель дроби 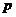 . .
| ||||||||
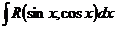
| Универсальная подстановка 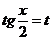 .
Если .
Если 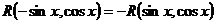 , то подстановка , то подстановка 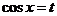 .
Если .
Если 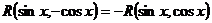 , то подстановка , то подстановка 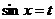 .
Если .
Если 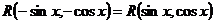 , то подстановка , то подстановка 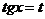 . .
| |||||||
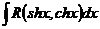
| Применяется подстановка 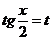 .
При этом .
При этом 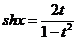 ; ; 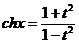 ; ; 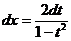 . .
| |||||||

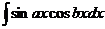
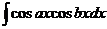
| Необходимо преобразовать произведение тригонометрических функций в сумму или разность, пользуясь одной из формул
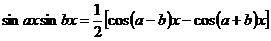 ; ;
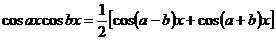 ; ;
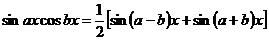 . .
| |||||||
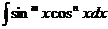 ,
где ,
где 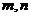 -целые числа -целые числа
| Если 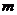 - нечетное положительное, то подстановка - нечетное положительное, то подстановка 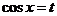 .
Если .
Если  - нечетное положительное, то подстановка - нечетное положительное, то подстановка 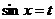 .
Если .
Если 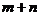 - четное отрицательное, то подстановка - четное отрицательное, то подстановка 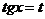 .
Если .
Если 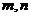 - четные неотрицательные, то применяют формулы: - четные неотрицательные, то применяют формулы:
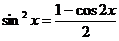 ; ; 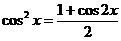 . .
| |||||||
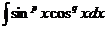 ,
где ,
где 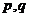 -рациональные числа -рациональные числа 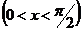
| Подстановкой 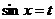 приводится к интегралу от биномиального дифференциала приводится к интегралу от биномиального дифференциала 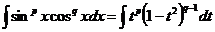 (см. п. 14). (см. п. 14).
| |||||||
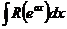
| Подстановкой  , преобразуется в интеграл от рациональной функции. , преобразуется в интеграл от рациональной функции.
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|