Лабораторная работа № 4. ИССЛЕДОВАНИЕ МЕТОДОВ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ. Постановка задачи №2.

Лабораторная работа № 4

ИССЛЕДОВАНИЕ МЕТОДОВ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ

Выполнила: Ванкова Ю.

Группа: 84-03 Вариант №2

Постановка задачи №1.

1. С целью исследования формул численного интегрирования вычислите определенный интеграл от функции f(x) на отрезке x Є [a, b], а также для «осциллирующих» функций f(x) + cos10x и f(x) + cos100x на том же отрезке xЄ [a, b] на равномерной сетке.

Вид функции f(x):

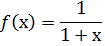
a=0, b=1.

В работе используйте формулы: прямоугольников, трапеций, Симпсона.

2.Краткие сведения по численному интегрированию:

a). Формула трапеций: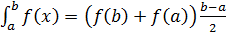

Оценка погрешности: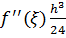

б). Формула Симпсона: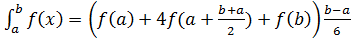

Оценка погрешности: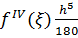

в). Формула прямоугольников: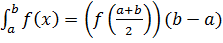

Оценка погрешности: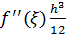

3.Точное значение интеграла:

I= 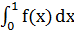= = 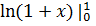0,693147180559945

I= 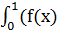+cos(10x)) 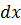= = 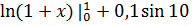0,638745069471008

I= 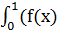+cos(100x)) 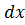= = 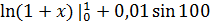0,688083524148848

4.Метод трапеции:

n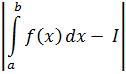
n1=10	0,0006242226
n2=100	6,2499E-06
n3=1000	6,249999E-08
n4=1000	6,25E-10
Порядок	2- й

n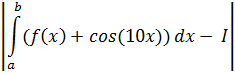
n1=10	0,00523513551265165
n2=100	5,1592572101522E-05
n3=1000	5,15851674154355E-07
n4=10000	5,15851061866357E-09
Порядок	2-й

n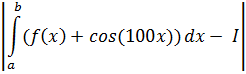
n1=10	0,0131773538576951
n2=100	0,000435425889234398
n3=1000	4,28291712228912E-06
n4=10000	4,28222065584905E-08
Порядок	2-й

Метод прямоугольников:

n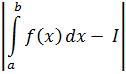
n1=10	0,000311820149984987
n2=100	3,1249316441162E-06
n3=1000	3,12499932597632E-08
n4=10000	3,12500580967878E-10
Порядок	2-й
n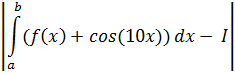
n1=10	0,00264647703478071
n2=100	2,57990910427219E-05
n3=1000	2,57926117130935E-07
n4=10000	2,57925347746379E-09
Порядок	2-й
n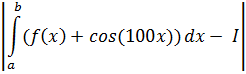
n1=10	0,0311546323154536
n2=100	0,000220430842495345
n3=1000	2,14172236945309E-06
n4=10000	2,1411131090332E-08
Порядок	2-й

Метод Симпсона:

n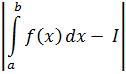
n1=10	1,94105170825409E-07
n2=100	1,95299332261811E-11
n3=1000	3,10862446895044E-15
n4=10000	2,33146835171283E-15
Порядок	4-й

n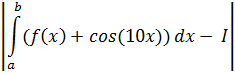
n1=10	1,92728523031871E-05
n2=100	1,86999449258707E-09
n3=1000	1,87627691161651E-13
n4=5000	8,88178419700125E-16
Порядок	4-й

n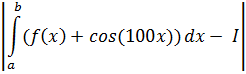
n1=10	0,0251622061628674
n2=100	1,81193191850504E-06
n3=1000	1,75871539553896E-10
n4=10000	1,40998324127395E-14
Порядок	4-й

Вывод:Методы трапеции и прямоугольников имеют 2-й порядок погрешности, а метод Симпсона 4-й.

Постановка задачи №2.

Реализовать и исследовать метод адаптивной квадратуры.

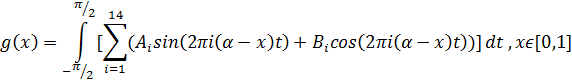
A_i	B_i
-0,02	0,16
0,8	-0,68
0,42	0,86
-0,98	-0,24
	-0,18
-0,38	-0,46
0,04	-0,66
-0,08	0,56
0,94	0,6
-0,92	0,72
0,46	0,4
-0,94	-0,14
0,7	-0,96
-0,08	0,3

α=0,84

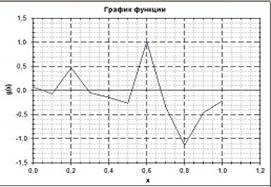Рассмотрим несколько графиков зависимости g(x) и Т(х) при числе разбиений интервала равном 40. При меньшем разбиении графики для Т(х) будут аналогичны, а функция g(x) будет колебаться с большей амплитудой например как на этом рисунке:

Графики при ε=0,1 Графики при ε=0,002

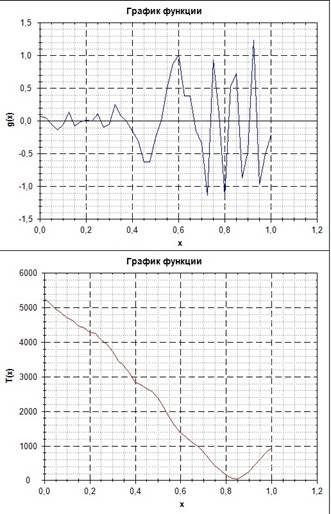
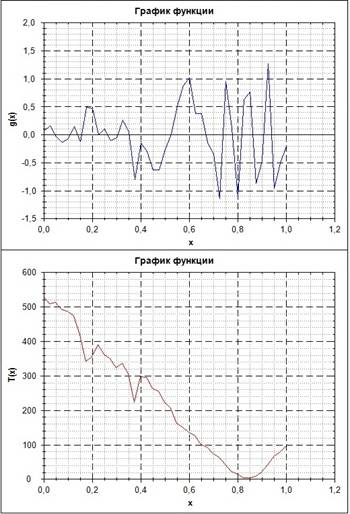
Графики при ε=0,0001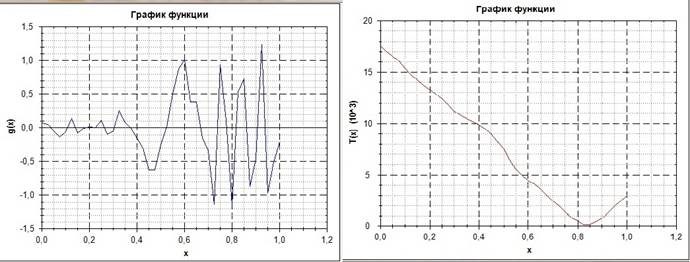

При уменьшении ε число рекурсий увеличивается. Точность вычисления интеграла этим методом находится в окрестности ε.

double VichInt(double a,double b,double x, double[] A,double[] B,double alfa, double eps,int iter, double met)

{

double I, I1, I2, IR1, IR2;

double c=(a+b)/2.0;

I=G(a, b, x, A, B, alfa, met);

I1=G(a, c, x, A, B, alfa, met);

I2=G(c, b, x, A, B, alfa, met);

double pv = Math.Abs(I - I1 - I2);

iter++;

if (pv < eps)

{

return I;

}

else {

IR1= VichInt (a,c,x, A,B,alfa, eps/2, iter, met);

IR2= VichInt (c,b,x, A,B,alfa, eps/2, iter, met);

return IR1+IR2;

}}

static public double G(double a, double b, double x, double[] A, double[] B, double alfa, double met)

{

double m=0;

if ( met == 1.0) m= (f(a, x, A, B, alfa)+f(b, x, A, B, alfa))*(Math.Abs(b - a))/2;

if ( met == 2.0) m= (f((a + b) / 2, x, A, B, alfa)) * (Math.Abs(b - a));

if ( met == 3.0) m= (f(a, x, A, B, alfa) + f(b, x, A, B, alfa) + 4 * f(a + Math.Abs(b - a) / 2, x, A, B, alfa)) * (Math.Abs(b - a)) / 6;

return m;

}