
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа 14. по теме: «Преобразование тригонометрических выражений». Материал к практической работе
Практическая работа 14
по теме: «Преобразование тригонометрических выражений»
Цель работы:
1) отработать навыки работы с таблицей значений тригонометрических функций;
2) закрепить навыки применения тригонометрических формул при вычислении значений тригонометрических функций и преобразовании выражений, содержащих тригонометрические функции.
Выполняя данную работу, студент должен знать:
· основные тригонометрические тождества;
· формулы сложения тригонометрических функций;
· формулы двойного аргумента;
· формулы приведения;
· формулы суммы, разности тригонометрических функций.
уметь:
· различать тригонометрические формулы;
· применять тригонометрические формулы при преобразовании и вычислении значений выражений.
Ход работы:
1. Изучить материал по теме практической работы.
2. Выполнить задания практического материала.
3. Выполнить тест (по вариантам).
Материал к практической работе
1. Найдите числовое значение выражения:
а) sin 0 + cos  + sin2
+ sin2  = воспользуемся таблицей значений тригонометрических
= воспользуемся таблицей значений тригонометрических
функций
= 0 + 0 + ( 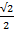 )2 =
)2 =  =
= 
Ответ:  .
.
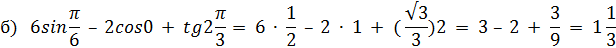
Ответ: 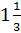 .
.
2. Найдите значения других трех основных тригонометрических функций, если:
а) sin α = - 0,8, 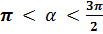
воспользуемся формулой 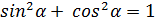 , из которой выражаем cos α
, из которой выражаем cos α
cos α = 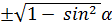 =
= 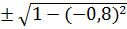 =
= 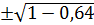 =
= 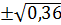 =
= 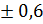
Т. к. угол α лежит в III четверти, то cosα 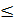 0.
0.
Получаем cosα = - 0,6.
Воспользуемся формулами 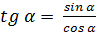 и ctg
и ctg 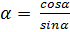
tgα = 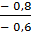 =
= 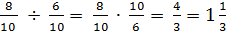
ctgα = 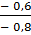 =
= 
Ответ: - 0,6; 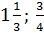 .
.
3. Вычислите cos 390  и tg 120
и tg 120 
воспользуемся формулами сложения
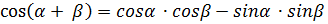 и
и 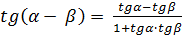
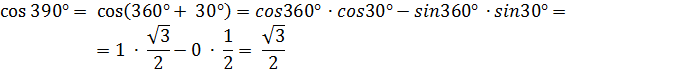
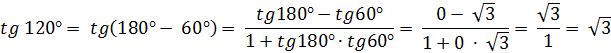
Ответ: cos 390  =
= 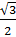 ; tg 120
; tg 120 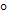 =
= 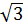 .
.
4. Упростить:
а) 
воспользуемся формулами свойств функции синус и косинус
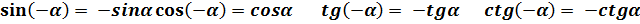
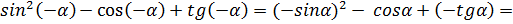

б) 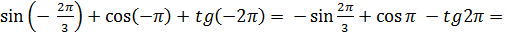

5. Упростите выражение:
а) 
для упрощения выражения вынесем – 1 за скобку и воспользуемся формулой сокращенного умножения а2 –b2 = (a – b)(a + b)
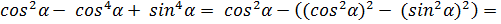
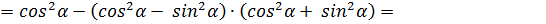
по основному тригонометрическому тождеству  получаем
получаем

б) 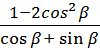
рассмотрим отдельно числитель дроби и воспользуемся тригонометрическими формулами двойного аргумента
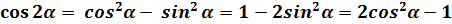
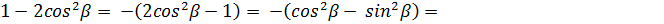
по формуле сокращенного умножения а2 –b2 = (a – b)(a + b)
перейдем от разности к произведению
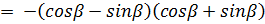
подставим получившееся выражение в числитель дроби
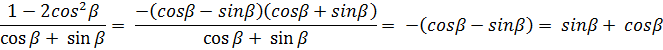
в) 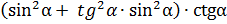
вынесем за скобки множитель 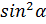 и воспользуемся формулой
и воспользуемся формулой 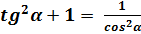
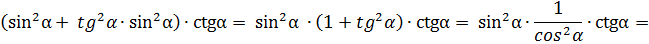
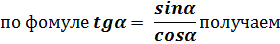
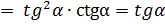
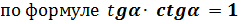
г) 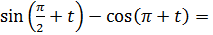 по формулам приведения
по формулам приведения 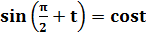 и
и
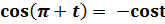
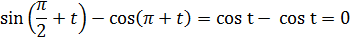
д) 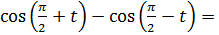 по формулам
по формулам 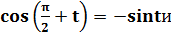
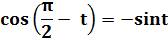

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|