Теоретические сведения.

Рабочий лист урока ДО

для группы № 196П Дата урока по расписанию 14.12.20

Преподаватель Алексеева Ирина Викторовна

Электронная почта Kolonchenko30@yandex.ru

Учебная дисциплина Математика

Тема практической работы № 1.1 : Перестановки. Размещения. Сочетания.

Доброе утро, обучающиеся!

Задание: Ознакомиться с теоретическим материалом и решить предложенные задания к следующему практическому занятию.

Обратная связь

Выполненную работу необходимо отправить на мою электронную почту

Файл выполненной работы необходимо назвать таким образом:

№ практической работы, Фамилия и имя, номер группы.

Теоретические сведения.

Комбинаторикойназывается раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Определение. Факториал числа 𝒏 - это произведение первых натуральных чисел до 𝒏 включительно: 𝒏! = 1 × 2 × 3 × … × 𝒏
0! = 1

Пример. Вычислить: 1) 3! = 1∙2∙3 = 6

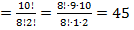
Определение. Комбинации из 𝒏 – элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.
Р_𝒏 = 𝒏 ! ,
где 𝒏 – число элементов, входящих в каждую перестановку.

Пример. Сколькими способами можно рассадить 5 человек за столом?

Решение. В данном случае n = 5. Используем формулу перестановок. Получим: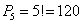

Ответ: 120 способами.

Определение.Комбинации из 𝒏 –элементов, по m – элементов, которые отличаются друг от друга или самими элементами, или порядком элементов, называются размещениями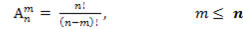

Пример.Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?

Решение.Выбираем из 7 разноцветных материалов 3 полосы для флага; порядок выбора имеет значение (флаги из трех одинаковых цветов, расположенных в разном порядке, - разные). Применим формулу размещений:

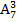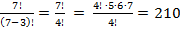
Ответ: 210 способами.

Определение. Комбинации, составленные из данных 𝒏 – элементов по m - элементов, которые отличаются хотя бы одним элементом, называются сочетаниями.

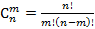
Пример. В ящике находится 15 деталей (n = 15). Сколькими способами можно взять 4 детали (m = 4)?

Решение: Каждая комбинация отличается хотя бы одним элементом. Применяя формулу сочетаний, получим:

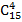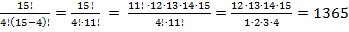
Ответ: 1365 способами

Решите самостоятельно следующие задачи:

1. В понедельник в пятом классе 5 уроков: музыка, математика, русский язык, литература и история. Сколько различных способов составления расписания на понедельник существует?

2. На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места 2 фотографии?

3. В хоровом кружке занимаются 9 человек. Необходимо выбрать двух солистов. Сколькими способами это можно сделать?