Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Обратные тригонометрические функции

Рабочий лист урока ДО

для группы № 208. Дата урока по расписанию 14.12.20

Преподаватель Алексеева Ирина Викторовна

Электронная почта Kolonchenko30@yandex.ru

Учебная дисциплина Математика

Тема практической работы № 1: Арксинус. Арккосинус. Арктангенс.

Доброе утро, обучающиеся!

Задание: Ознакомиться с теоретическим материалом и решить предложенные задания к следующему практическому занятию.

Обратная связь

Выполненную работу необходимо отправить на мою электронную почту

Файл выполненной работы необходимо назвать таким образом:

№ практической работы, Фамилия и имя, номер группы.

Обратные тригонометрические функции

Предположим, что число a удовлетворяет неравенству 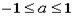. Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:

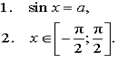
Предположим, что число a удовлетворяет неравенству 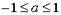. Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:

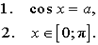
Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:

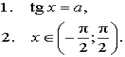
Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:

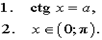
Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:

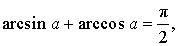
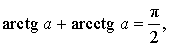
arcsin (– a) = – arcsin a ,

arccos (– a) = π – arccos a ,

arctg (– a) = – arctg a ,

arcctg (– a) = π – arcctg a .

Обратными тригонометрическими функциями называют функции:

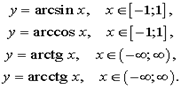
Графики этих функций изображены на рисунках 1, 2, 3, 4.

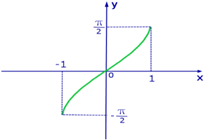
Рис. 1. График функции y = arcsin x