
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Составление и решение обратной задачи
1. Какую подготовительную работу, по вашему мнению, целесообразно провести перед введением типовых задач на движение? Какие методические приемы может использовать учитель при разъяснении младшим школьникам понятия «скорость движения» и ознакомлении их с зависимостями между величинами скорость, время, расстояние? С какой целью при решении простых задач на движение используется прием составления и решения обратных задач? (В ответе используйте материал статьи В.Н. Рудницкой «Формирование у школьников понятия «скорость». //Начальная школа 1993 № 1.)
Подготовительная работа к решению задач связанных с движением, предусматривает: обобщение представлений детей о движении, знакомство с новой величиной – скоростью, раскрытие связей между величинами: скорость, время, расстояние.
С целью обобщения представлений детей о движении полезно провести специальную экскурсию по наблюдению за движением транспорта, после чего провести наблюдение в условиях класса, где движение будут демонстрировать сами дети. На экскурсии и во время работы в классе пронаблюдать за движением одного тела и двух тел относительно друг друга. Так, одно тело (машина, человек, и т.п.) может двигаться быстрее и медленнее, может остановиться, может двигаться по прямой или кривой. Два тела могут двигаться в одном направлении, а могут двигаться в противоположных направлениях: либо приближаться друг к другу (двигаясь на встречу одно к другому), либо удаляясь одно от другого. Наблюдая указанные ситуации в условиях класса, надо показать детям, как выполняются чертежи: расстояние принято обозначать отрезком; место отправления, встречи, прибытия обозначают либо черточкой, либо флажком; направление движения указывают стрелкой.
Важным результатом ознакомления учащихся с простыми задачами на движение в одном направлении является усвоение простейших формул, связывающих такие величины, как скорость, время и расстояние (v, t, s ).
Рассмотрим основные пути усвоения зависимости между этими величинами, характеризующими равномерное движение.
На первом из уроков необходимо, опираясь на жизненный опыт и наблюдения учащихся обратить внимание детей на то, что некоторые предметы могут двигаться быстрее и медленнее. Например, велосипедист может обогнать пешехода, автомобиль – велосипедиста, самолет – автомобиль и т.д. Предметы могут двигаться равномерно. Так, например, пешеход может проходить за каждый час по 3 км; автомобиль может проезжать за каждый час по 100 км; бегун может пробегать за каждую секунду по 8 м и т.д. В этом случае говорят, что скорость (соответственно) пешехода – 3 км в час (записывают 3 км/ч), автомобиля 100 км/ч, бегуна – 8 м/с.
При ознакомлении со скоростью необходимо так организовать работу учащихся, чтобы они сами нашли скорость своего движения пешком. Дети проходят расстояние за одну минуту. Учитель же сообщает, что расстояние, которое ученик прошел за 1 минуту называется скоростью. Учащиеся называют свои скорости. Затем учитель называет скорости некоторых видов транспорта и подводит детей к выводу: скорость движения – это расстояние, которое проходит движущийся предмет за единицу времени. После этого рассматриваются простые задачи, на основании которых делается вывод, что для нахождения скорости движения предмета, нужно расстояние, которое прошел предмет, разделить на время, затраченное для этого. Если скорость обозначить буквой v, путь – буквой s, а время - буквой t, то можно записать этот вывод в виде формулы: v= s : t.
На последующих уроках с помощью решения соответствующих простых задач устанавливается, что расстояние равно скорости, умноженной на время: s = v *.t.
На основе решения следующего вида задачустанавливается, что время равно расстоянию, деленному на скорость: t = s : v. Можно обратить внимание учащихся на связь между этими тремя формулами (например, последняя формула может быть выведена из первой)
В результате решения соответствующих простых задач ученики должны усвоить такие связи:
если известны расстояние (s) и время (t) движения, то можно найти скорость (v) действием деления: v=s: t
если известны скорость (v) и время (t) движения, то можно найти расстояние (s)действием умножения: s=v*t
если известны расстояние (s) и скорость (v), то можно найти время (t) движения действием деления: t=s: v.
Таким образом, специфика этих задач обуславливается введением такой величины, как скорость движения, а также использованием при их решении схем, которые отражают не отношения между величинами, а процесс движения и во многом облегчают поиск решения.
Методические приемы:
-преобразование задач (изменение отношений между данными и искомыми
в задаче, изменение частей или данных в задаче);
-сравнение последовательности составления моделей к задачам на
движение, на пропорциональную зависимость, к произвольным составным
задачам;
-сравнение логики или последовательности построения рассуждений по
задачам различным типов;
-составление различных моделей, текстов, схем рассуждений по одной и
той же задаче на движение;
-выбор среди предложенных моделей, схем рассуждения тех, что
соответствуют данной задаче;
- решение задач с недостающими данными или с недостающей частью условия;
-воспроизведение или составление текстовых задач по моделям и схемам;
-анализ неверной модели или схемы с последующим преобразованием.
Составление и решение обратной задачи
Этапы обучения составления и решения обратной задачи:
I. Подготовительная работа к введению приема:
Цель: сформировать умения, необходимые для осуществления приема проверки.
II. Проверка решения под руководством учителя.
Учитель после неверно решенной задачи проговаривает способ проверки (в неявном виде).
III. Усвоение способа проверки и самостоятельное его использование.
Цель: запоминание детьми последовательности действий для проверки и формирование умения использовать самостоятельно способ проверки. Овладение данными способами проверки решения задачи способствует в первую очередь развитию одного из важнейших компонентов учебной деятельности – действия самоконтроля. В ходе проверки развиваются три его вида – прогнозирующий, процессуальный (пошаговый) и итоговый.
Введения обратных задач на движение позволяет детям самостоятельно найти решение, поскольку задача нового вида будет получена из задачи, уже решенной детьми.
2. Составьте всевозможные простые и составные задачи на движение. М4М ч.2 с.10-11. Какова, по вашему мнению, цель урока, проводимого по этим страницам учебника? Опишите организацию деятельности учащихся при решении этих задач, используя приемы: выбор схемы, постановка или выбор вопроса к данному условию, условие с недостающими данными и др.

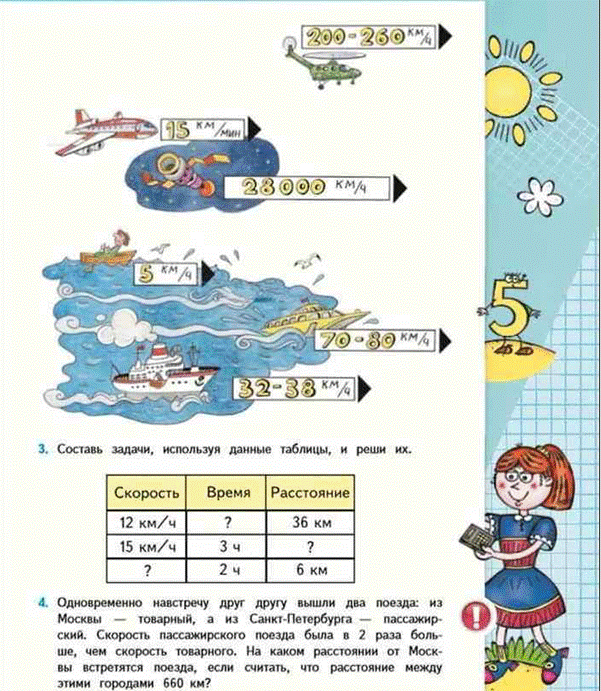
1)Человек пешком движется со скоростью 5 км/ч. Какова может быть скорость человека на лошади, если известно, что она в 3 раза больше скорости пешком?
2)Турист прошел 8 км со скоростью 4 км/ч и 12 км со скоростью 6 км/ч. Сколько времени на путь затратил турист?
3) Два лыжника выехали одновременно со старта. На сколько километров первый лыжник обогнал второго за 20 минут пути, если скорость первого лыжника 5 м/с, а второго 3 м/с?
4)Мотоциклист проехал дорогу из одного города в другой со скоростью 70 км/ч. Сколько времени ехал мотоциклист, если расстояние между городами 420 км?
5) Из одного города в другой выехал красный автомобиль со скоростью 70 км/ч, а через 1 час после него по тому же маршруту выехал синий автомобиль со скоростью 90 км/ч. Определите, смог ли догнать синий автомобиль красный через 3 часа пути?
6)Из пункта А в пункт Б выехал пассажирский поезд со скоростью 80 км/ч, а ему навстречу выехал товарный поезд со скоростью 60 км/ч. Через сколько часов встретятся поезда, если расстояние между пунктами 420 км.
7)Мама с дочкой пошли на рынок со скоростью 30 м/мин, а возвращались со скоростью 40 м/мин. Сколько времени потратила мама с дочкой на поход в магазин и обратно, если расстояние от дома до магазина составляет 360 м?
8)Полет из точки А в точку Б занимает 3 ч. Найдите расстояние между точками, если скорость самолета 15 км/ч?
9)Скорость спутника составляет 28000 км/ч. Какова может быть скорость вертолета, если известно, что она меньше скорости спутника в 140 раз.
10)Известно, что для того, чтобы доплыть из одного острова на другой нужно плыть: 4 ч на лодке, 6 ч на катере и 12 ч на теплоходе. Найдите расстояние от одного острова до другого, если известно, что скорость лодки 5 км/ч, скорость катера 70 км/ч, а скорость теплохода 35 км/ч.
Целью этого урока является научить детей самостоятельно составлять задачи с величинами “скорость”, “время”, “расстояние”, познакомить ребят со скоростями реальных различных транспортов,животных и людей, работа над навыком решения задач на движение.
3. Приведите примеры различных типовых и нетиповых составных задач на движение, которые представлены в различных учебниках математики для начальных классов. Могут ли задачи на движение в то же время быть задачами на нахождение 4-го пропорционального, на нахождение неизвестного по двум суммам или двум разностям? Приведите соответствующие примеры. Какие виды моделей наиболее эффективны при работе с такими задачами на движение? Приведите примеры разных моделей к задачам на движение.
Программа Моро
Типовые задачи:
задача на нахождение 4 пропорционального

М4Мч2 стр 7 номер 22
| Скорость | Время | Расстояние | |
| Теплоход Моторная лодка | 36 км/ч ? | 4 ч 9 ч | Одинаковое |

М4Мч2 стр 27 номер 89
| Скорость | Время | Расстояние | |
| 1 путь 2 путь 3 путь | Одинаковая | 5 мин 40 мин 60 мин | 6000 м ? ? |

М4Мч2 стр60 номер 227
| Скорость | Время | Расстояние | |
| Первый день Второй день | Одинаковая | 8 ч 6 ч | 350 км ? |
Задача на нахождение неизвестного по двум суммам

М4Мч2 стр60 номер 227
| Скорость | Время | Расстояние | |
| 1 день 2 день | Одинаковая | 8 ч 6 ч | ? ? |
Задачи на нахождение неизвестного по двум разностям

М4Мч2 стр 47 номер 175
| Скорость | Время | Расстояние | |
| 1 самолёт 2 самолёт | Одинаковая | 4 ч 6 ч | ?на 1400 км меньше ? |

М4Мч2 стр60 номер 227
| Скорость | Время | Расстояние | |
| 1 день 2 день | Одинаковая | 8 ч 6 ч | ? На 50 км больше ? |
Программа Истоминой
Нетиповые задачи:

М4Ич2 стр 46 номер 158
| Скорость | Время | Расстояние | |
| 1 день 2 день | 6 км/ч 6 км/ч | ? ? | 24 км 30 км |

М4Ич2 стр 62 номер 213
| Скорость | Время | Расстояние | |
| 1 пешеход 2 пешеход | 6 км/ч 4 км/ч | 3 ч 3 ч | ? ? |

М4Ич2 стр 62 номер 214
| Скорость | Время | Расстояние | |
| Дорога из города на дачу Дорога из дачи в город | 90 км/ч 60 км/ч | 2 ч ? | ? ? |
Типовые задачи
Задачи на нахождение 4 пропорционального

М4И ч2 стр 69 номер 246
| Скорость | Время | Расстояние | |
| 1 путь 2 путь | Одинаковая | 7 ч ? | 560 км 280 км |

М4Ич2стр 71 номер 255
| Скорость | Время | Расстояние | |
| 1 путь 2 путь | Одинаковая | 1,5 часа 2 ч | 810 км ? |
Задача на нахождение неизвестного по двум суммам

М4Ич2 стр 47
| Скорость | Время | Расстояние | |
| Первый день Второй день | ? Одинаковая | 
| 18 км 27 км |
Задачи на нахождение неизвестного по двум разностям

М4Ич2 стр 66 номер 229
| Скорость | Время | Расстояние | |
| 1 турист 2 турист | Одинаковая | ?на 40 мин меньше ? | 8 км 12 км |
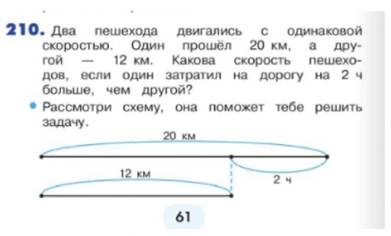
М4Ич2 стр 61
| Скорость | Время | Расстояние | |
| 1 пешеход 2 пешеход | ? Одинаковая | ? На 2 ч больше ? | 20 км 12 км |
ПРОГРАММА АРГИНСКОЙ
М3А ч2 стр 77- простая задача и дальше составная нетиповая задача

| Скорость | Время | Расстояние | |
| Катер Теплоход | ? ? | 6 ч 8 ч | 144 км Одинаково 144 км |
М3А ч2 стр 87- решение составной нетиповой задачи

| Скорость | Время | Расстояние |
| 85 км/ч | (12 ч- ⅙) | ? |
М3А ч2 стр 100- составная нетиповая задача

| Скорость | Время | Расстояние | |
| Лодка Катер | 
| 3 ч | 27 км ? |
М3А ч2 стр 105- типовая задача на нахождение четвертого пропорционального четвертого вида

| Скорость | Время | Расстояние |
| 96 км/ч ? | 4 ч 6 ч | одинаково |
М3А ч2 стр 120 - нетиповая задача

| Скорость | Время | Расстояние | |
| По течению Против течения | 
| 9 ч ? | 108 км |
М3А ч2 стр - нетиповые составные задачи

М4Ач1с135№261-
Задачи на движение на нахождение неизвестного по двум разностям (1-2 вид)

4. Какую подготовительную работу необходимо провести прежде, чем познакомить учащихся с новым видом задач на движение – на движение в противоположных направлениях (на сближение и удаление друг от друга)? Приведите примеры таких заданий, подберите из учебников или придумайте самостоятельно, Какие методические приемы может использовать учитель при ознакомлении младших школьников с задачами на движение в противоположных направлениях? Какие новые понятия вводятся? Какие виды таких задач можно выделить?
Задача на движение навстречу друг другу, на сближение
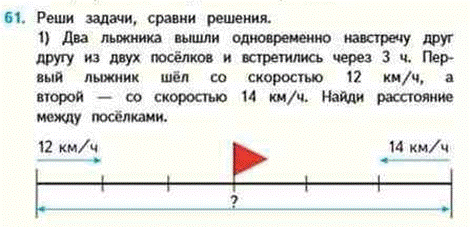
М4Мч2 стр 16 номер 61
2 вид – на нахождение времени движения. М4М ч.2 с.16.
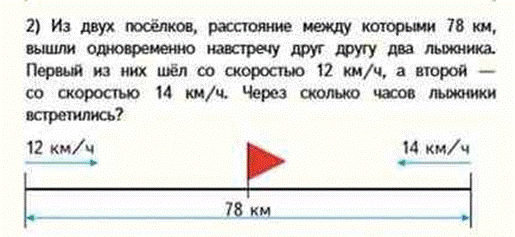
3 вид – на нахождение скорости одного из движущихся. М4М ч.2 с.16.
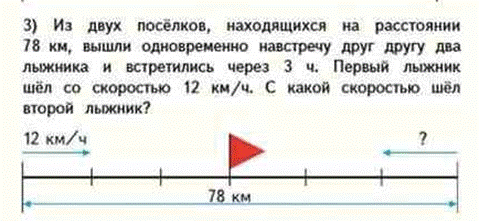
Задача на движение в противоположные стороны, удаление
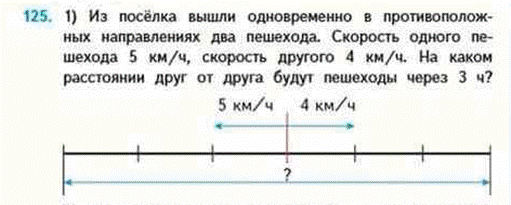
М4Мч2 стр 33 номер 125
Аналогично предыдущему случаю разбирают. что такое скорость удаления – это расстояние, на которое удаляются движущиеся объекты за единицу времени. Она равна сумме скоростей.
К такой задаче составляются две обратные, на нахождение времени и скорости. М4М ч.2 с.33.
2 вид - на нахождение времени
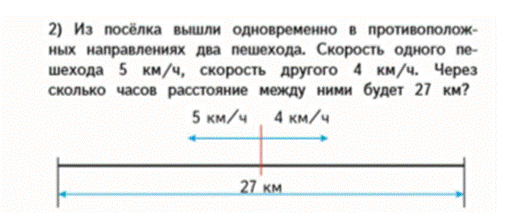
М4М ч2 с33
3 вид - на нахождение скорости
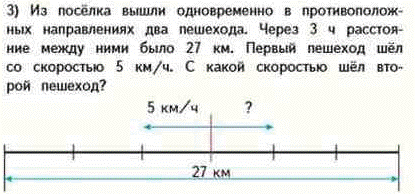
Задачи на движение в одном направлении, Нахождение скорости обгона

М4Мч2стр 60 номер 206
М4А ч1 стр 22 - нахождение расстояния

М4А ч1 стр 37- нахождение времени

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|