Лекция 21. Тема «Определение степенной, тригонометрической, показательной и логарифмической функции». Степенные функции. Тригонометрические функции. Показательные функции

Стр 1 из 2Следующая ⇒

Лекция 21

Тема «Определение степенной, тригонометрической, показательной и логарифмической функции»

Цель:систематизировать и углубить знания о видах функций и навыки построения их графиков.

План лекции:

1. Степенные функции.

2. Тригонометрические функции.

3. Показательные функции, их свойства и график.

4. Логарифмические функции, их свойства и график.

Степенные функции

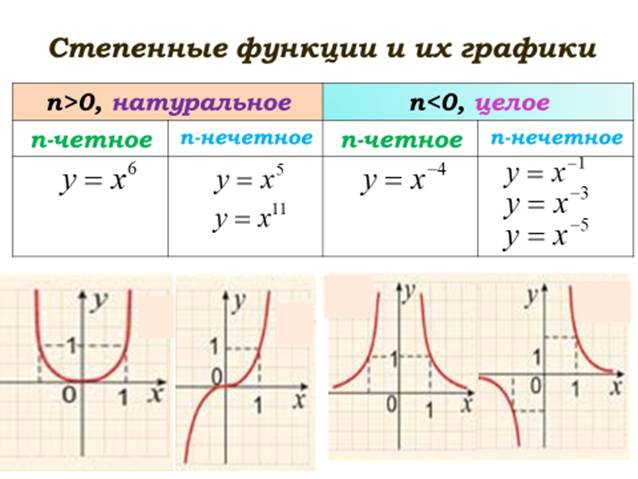
Определение. Степенной функцией называется функция, заданная формулой y= xⁿ, где x-аргумент, n -данное число и допустимыми значениями считаются все те значения аргумента, при которых выражение xⁿимеет смысл.

Если n=1,то y=x (графиком которой является прямая – биссектриса 1 и 3 координатных углов).

Примеры графиков степенных функций, соответствующих различным показателям степени, представлены на рисунках.

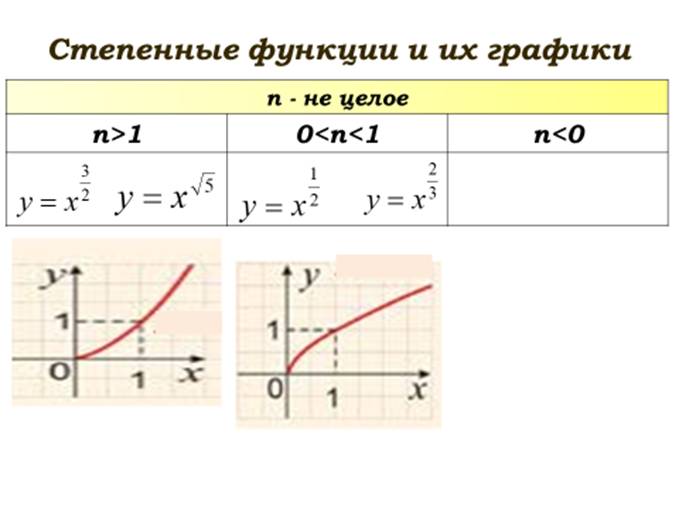
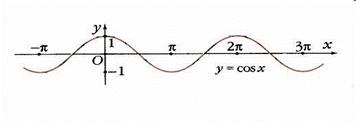
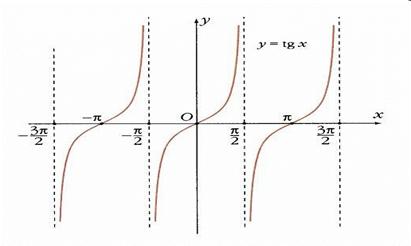
Тригонометрические функции

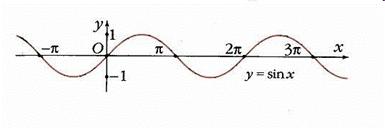
Тригонометрические функции и их свойства мы уже рассматривали в лекции 16.

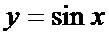
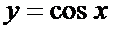
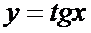
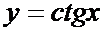
Показательные функции

В практике часто используются функции y=2^х,y=10^х,y= 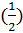^х,y=(0,1)^х и т. д., т. е. функция вида y=a^х, где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение.Функция, заданная формулой y=a^х (где a>0,a≠1), называется показательной функцией с основанием a.

12 Следующая ⇒