Хелпикс

Главная

Контакты

Случайная статья



ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. УРОК Методы решения тригонометрических уравнений.. Метод разложения на множители. Разложение на множители



ДИСТАНЦИОННОЕ ОБУЧЕНИЕ

УРОК Методы решения тригонометрических уравнений.

Метод разложения на множители

 Цели: изучить методы решения тригонометрических уравнений ; научиться применить метод разложения на множители для решения различных тригонометрических уравнений.

Решение тригонометрического уравнения состоит из двух этапов:

1. преобразование уравнения для получения его простейшего вида

2. решение полученного простейшего тригонометрического уравнения.

Разложение на множители

.

Алгоритм:

1. Применить тригонометрические формулы. Перенести все в правую часть. Слева должен быть 0.

2. Разложить на множители. Приравнять каждый множитель к 0.

3. Решить простейшие тригонометрические уравнения

 

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

 

 Р е ш е н и е . Перенесём все члены уравнения влево:

 

sin x + cos x – 1 = 0 ,

 

Преобразуем и разложим на множители выражение в  левой части уравненияLформулы синуса и косинуса двойного угла)

 

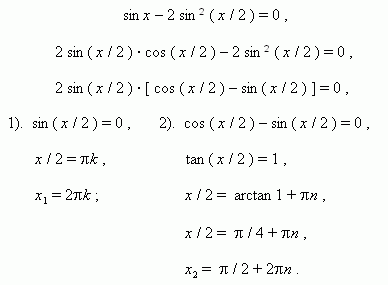
П р и м е р 2.

Решить уравнение: cos 2 x + sin x · cos x = 1.

 

 Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

 

sin x · cos x – sin 2 x = 0 ,

 

sin x · ( cos x – sin x ) = 0 ,

 

Отсюда 2 варианта решения:

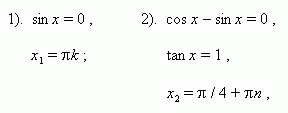
П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1.

Р е ш е н и е . cos 2x + cos 6x = 1 + cos 8x ,

 

2 cos 4x cos 2x = 2 cos ² 4x ,

 

cos 4x · ( cos 2x – cos 4x ) = 0 ,

 

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 2). sin 3x = 0 , 3). sin x = 0 ,

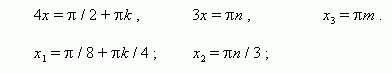
Решить уравнения:

1.

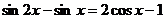
2.

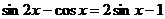
3.

4.

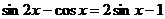
5.

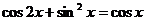
6.

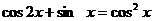
7.

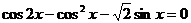
8.

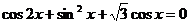
Домашнее задание: Параграф 36, № 628, 629.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.